This EJS Open Source Physics Gyroscope Model is created by Wolfgang Christian!
slightly edited only the interface by lookang.

This is the one of the most awesome physics driven gyroscope made in EJS..
i remixed cos some Singapore navy instructor angcl72@yahoo.com.sg requested for teaching materials.
enjoy!

EJS Open Source Physics Gyroscope Model is created by Wolfgang Christian http://weelookang.blogspot.sg/2013/07/gyroscope-by-wolfgang-christain.html author: Wolfgang Christian lookang only changed slightly the interface. download: https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejs_Gyroscopewee.jar original version: http://www.compadre.org/osp/items/detail.cfm?ID=10681

the other gyroscope are:

1. http://www.compadre.org/osp/items/detail.cfm?ID=10681 by Wolfgang Christian
2. http://faculty.ifmo.ru/butikov/Applets/Gyroscope.html by Eugene Butikov
3. http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=2141.0 by Fu-Kwun Hwang

slightly edited only the interface by lookang.
changes made:
added dropmenu referencing Eugene Butikov work
axis shifted
control redesign to suit my style

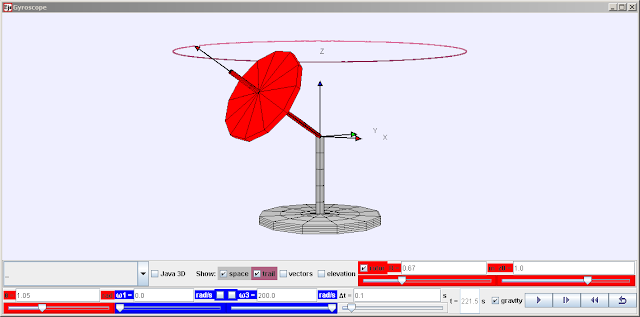
       Gyroscope

The Gyroscope example computes and displays the dynamics of gyroscope under the influence of gravitational torque acting on the center of mass.  The gyroscope is supported at one end and given an initial angular velocity component about its axis of symmetry and a component perpendicular to its axis of symmetry.  The numerical solution shows the motion for all initial conditions including zero initial angular momentum. The model is designed to show the cycloidal motion (precession and nutation) of the gyroscope axle when the initial angular velocity is large.  Users can vary the position and radius of the spinning mass as well as the initial angle and can display the angular momentum L, angular velocity ω, and torque N vectors.  A second window shows the elevation angle of the axle and the angular momentum vector.
 
Units are chosen such that the total mass M and the acceleration of gravity g are one.  The rotor is an ellipsoid with a uniform mass distribution and with major axes 2*R and minor axis R/5.  The ellipsoid's moment of inertia through the center of mass is 4MR²/5 about the major axes and 26MR²/125 about the minor axis.

Related Models

The following EJS models are described in Chapter 17 of the EJS adaptation of An Introduction to Computer Simulation Methods available in the ComPADRE digital library.
 

• Affine Transformation in 2D: Shows how homogeneous coordinates are used in two dimensions.
• Affine Transformation in 3D: Shows how homogeneous coordinates are used in three dimensions.
• Euler Angle Demo:  Displays the orientation of a rigid body subject to three Euler angle rotations.
• Quaternion Demo:  Displays the orientation of a rigid body subject to a quaternion rotation.
• Rotation About a Fixed Axis: Computes the angular momentum of a box attached to an axle.
• Feynman Plate: Computes the wobble of a spinning plate using a simple quaternion rate equation.
• Free Rotation: Computes and displays the trajectory of a rigid body rotating about its center of mass in the absence of external torque.
• Gyroscope:  Computes and displays the dynamics of a gyroscope under the influence of a gravitational torque.

 

References:

• R. Feynman, R. Leighton, and M. Sands, The Feynman Lectures in Physics vol 1, p20-5 to 20-8, Addison-Wesley (1963)
  
• Svilen Kostov, "It has to Go Down a Little, In Order to Go Around-- Revisiting Feynman on the Gyroscope," The Physics Teacher, (in press).
  
• Herbert Goldstein, Charles P. Poole, and John L. Safko, Classical Mechanics, third edition, Addison-Wesley (2002). Chapter 4 discusses the kinematics of rigid body motion.
  
• Dennis C. Rapaport, The Art of Molecular Dynamics Simulation, second edition, Cambridge University Press (2004). Chapter 8 discusses the molecular dynamics of rigid molecules using quaternions.
  
• Harvey Gould, Jan Tobochnik, and Wolfgang Christian, An Introduction to Computer Simulation Methods, third edition, Addison Wesley (2007).  Chapter 17 describes the quaternion-based numerical algorithm used in this model.
  

Credits

The Gyroscope example was developed by Wolfgang Christian using the Easy Java Simulations (EJS) modeling tool version 4.3.  You can examine and modify the model for this simulation if you have EJS installed by right-clicking within the program and selecting "Open Ejs Model" from the pop-up menu. 
 

Information about EJS is available at: <http://www.um.es/fem/Ejs/> and in the OSP ComPADRE collection <http://www.compadre.org/OSP/>.  


Text taken from

       Rigid Body Dynamics

The behavior of a rigid body rotating about a fixed point is determined by
 
N = dL/dt
 
where the angular momentum L and torque N are vectors. For a constrained body, such as gyroscope, the fixed point is usually taken as the point of support.  The angular momentum L is expressed in terms of the angular velocity ω and the moment of inertia tensor I as L=Iω where ω is a vector.  Substituting the angular momentum expression into the rate expression gives the rotational equivalent of Newton's second law.
 
N = d( Iω)/dt

The difficulty in solving this equation is that the moment of inertia tensor I is not constant in the inertial reference frame (space frame).  This computational difficulty is overcome by transforming the rate equation into a non-inertial rotating coordinate system that is aligned with the principal axes of the rotating gyroscope.  Although the moment of inertia is constant and diagonal in this reference frame, the transformation introduces an additional term into the rate equation.
 
N = I dω/dt + ω^(Iω) where ^ is cross product

The transformed rate equation is Euler's equation for rigid body motion and is usually written in component form to highlight the importance of the diagonal inertia matrix elements I₁, I₂, and I₃.
 
N1 = I1d(ω1)/dt - (I2-I3)ω2ω3
N2 = I2d(ω2)/dt - (I3-I1)ω3ω1
N3 = I3d(ω3)/dt - (I1-I2)ω1ω2
 
We label the vector components in the rotating system as the 123-axis components in order to avoid confusion with the fixed (spatial) xyz-axis components.
 

The solution of Euler's equation is not easy because the orientation of the gyroscope must be tracked and because the gravitational torque must be constantly transformed from the space frame to the body frame as the solution advances.  Analytical solutions exist only for special conditions.  Fortunately, EJS provide the tools needed for an accurate numerical solution.  In this model, the gyroscope orientation is expressed using a quaternion as described in the references and the quaternion rate equation is solved using an adaptive ODE solver.  This quaternion is used to transform the gravitational force into the gyroscope body frame and to orient the view elements, such as the gyroscope body, after every time step but the algebra needed to perform these transformations is built into the EJS Elements and hidden from the user.