Kepler’s Third Law
It was stated that the gravitational force acting on a satellite in orbit
is the centripetal force to keep it in circular motion.
i.e. ΣF = mrω2
recalling in circular motion,
Hence,
can be simplified to an equation involving T and r
This is the Kepler’s Third Law, which states that the square
of the period of an object in circular orbit (i.e. the
gravitational force acts as the centripetal force) is directly
proportional to the cube of the radius of its orbit. T2
α r3
Note:
• The Kepler’s Third Law is only applicable to masses in circular
orbit, whereby the gravitational force is the only force acting on it to
act as its centripetal force.
Complete ICT inquiry worksheet 2 to build your conceptual understanding
on the Kepler’s Third Law.
This series of screenshot serves to guide your inquiry
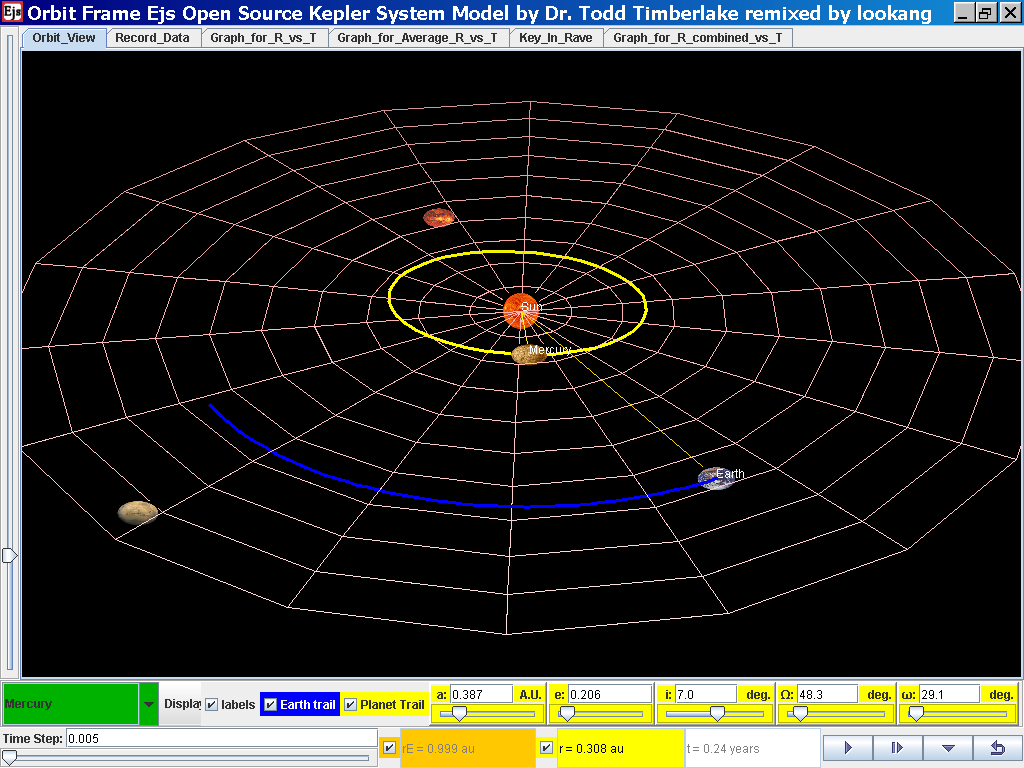
Select from the drop-down menu the planet, say Mercury to show the
orbital radius and click play.
Click Pause the simulation when the planet Mercury is almost at the time
of 1 complete cycle or period T.
Click Step to fine tune your determination of period T, say t =0.24 years
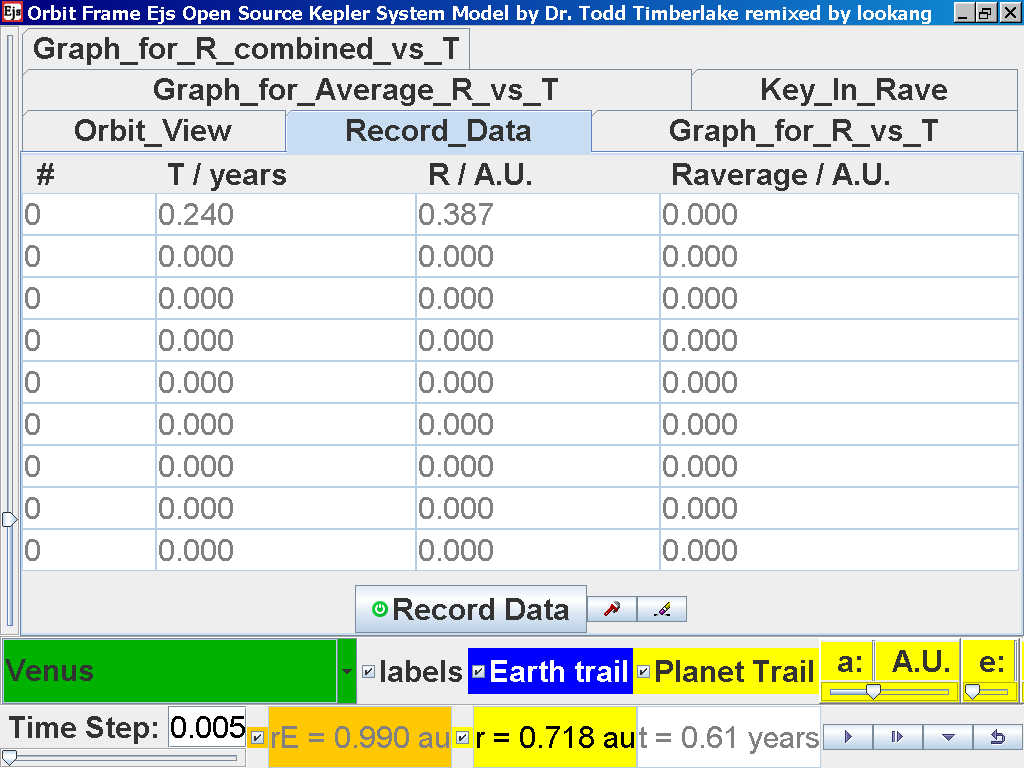
Click on the adjacent tab Record_Data and select Record Data button to
store this data on the mean radius Rm and period (time for one complete
cycle) T of motion.
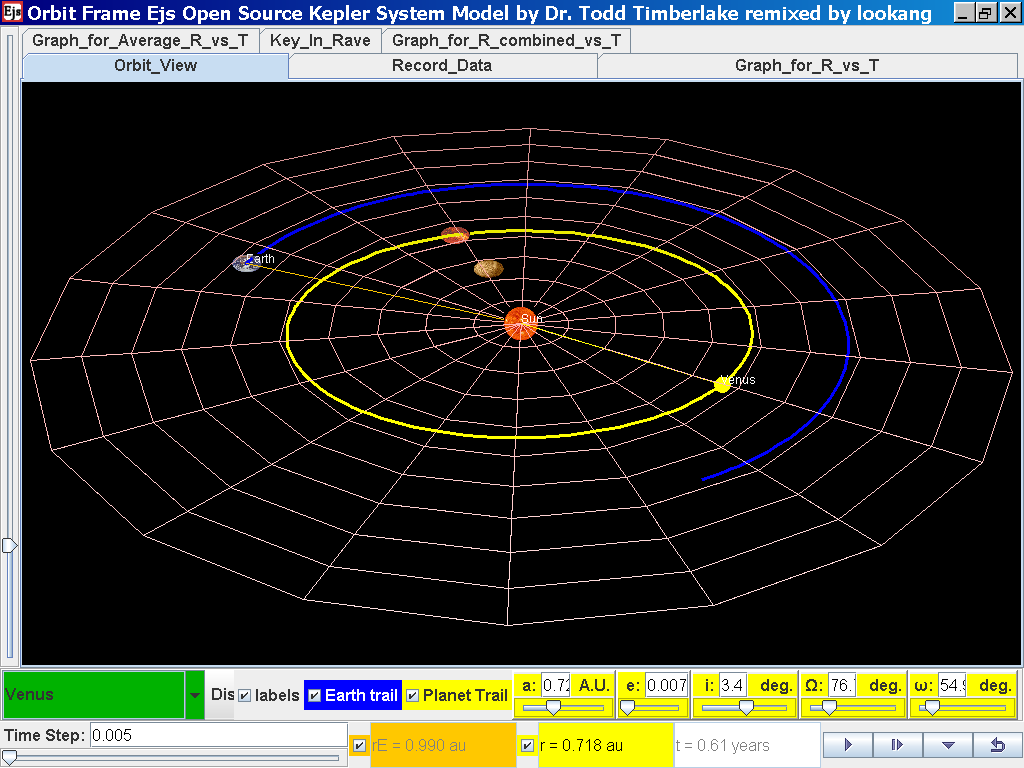
Click back to the Orbit_View and to go to the next planet to collect data,
select from the drop down menu again and select the next planet say Venus.
Play the simulation for one complete cycle.
again click on the next tab Record_Data and select Record_Data.
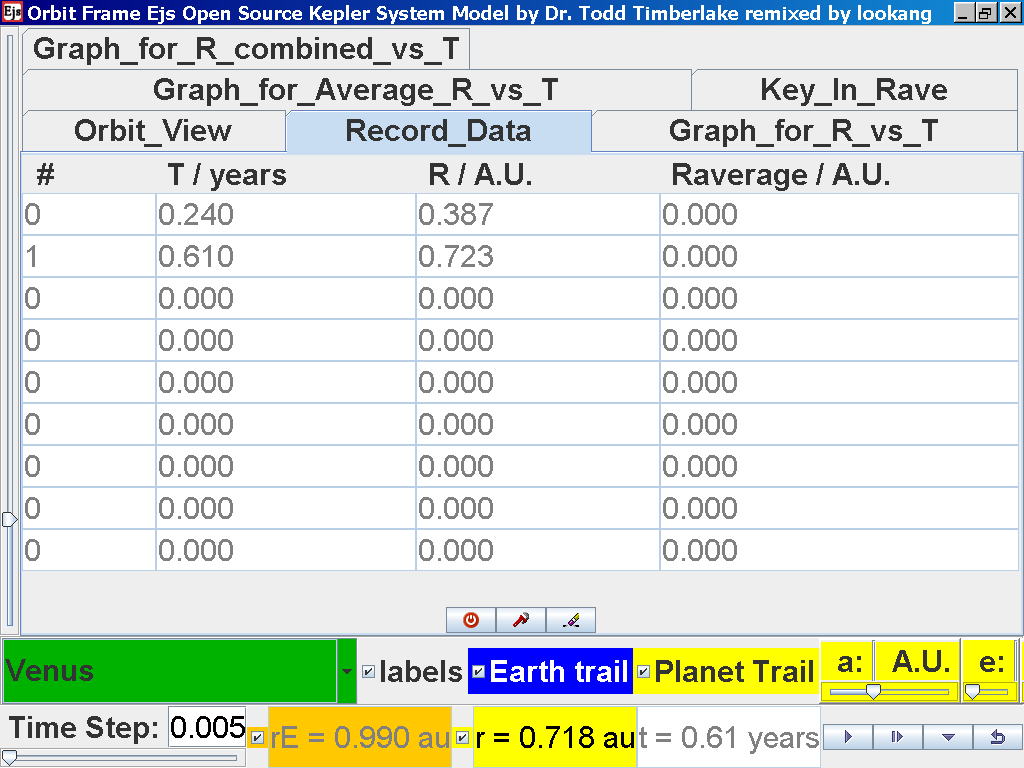
Now the steps need to be repeated for the rest of the planets. Click back to
the Orbit_View and to go to the next planet to collect data, select from the
drop down menu again and select the next planet say Earth. Play the
simulation for one complete cycle.
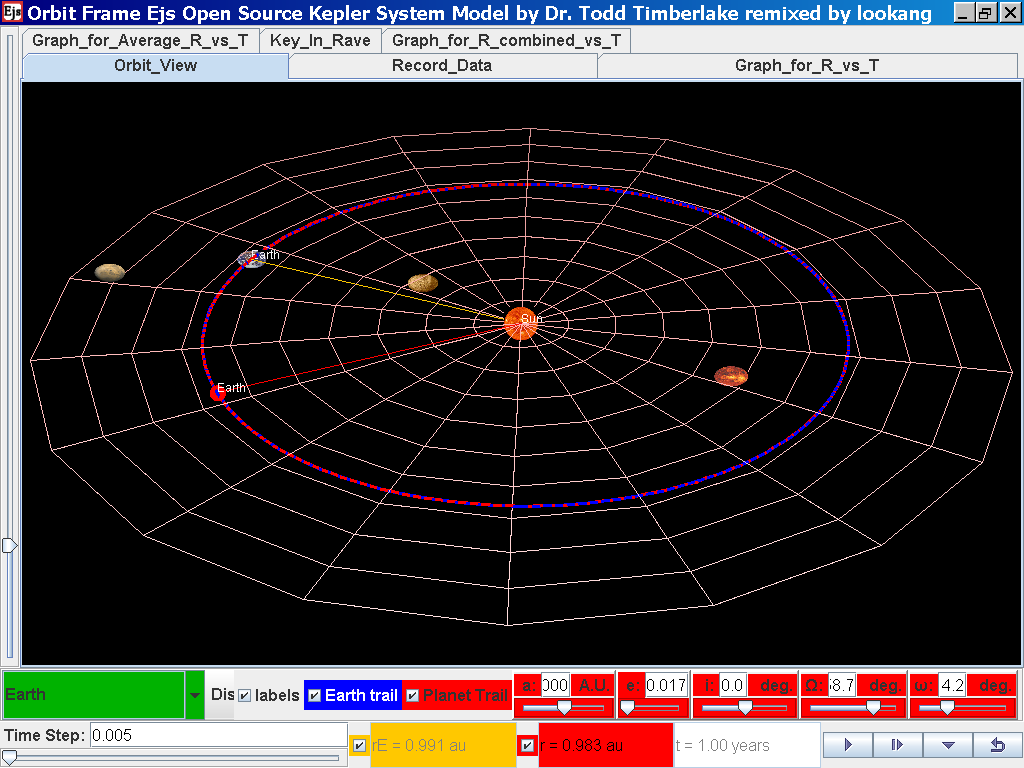
again click on the next tab Record_Data and select Record_Data.
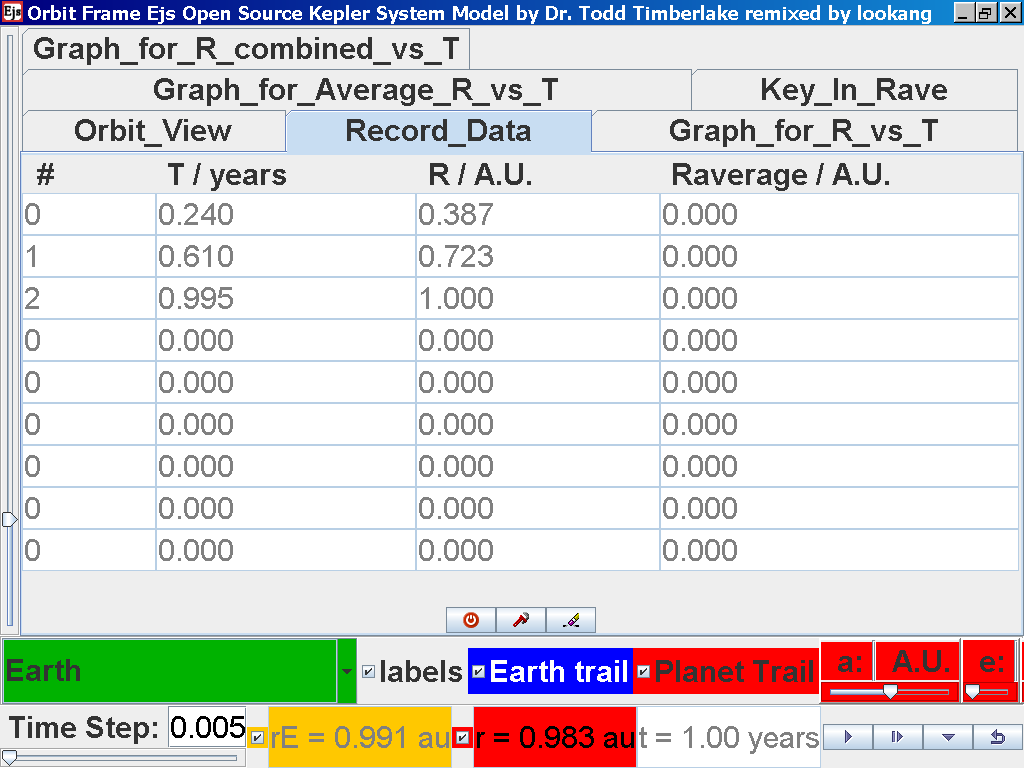
Click back to the Orbit_View and to go to the next planet to collect data,
select from the drop down menu again and select the next planet say Mars.
Play the simulation for one complete cycle
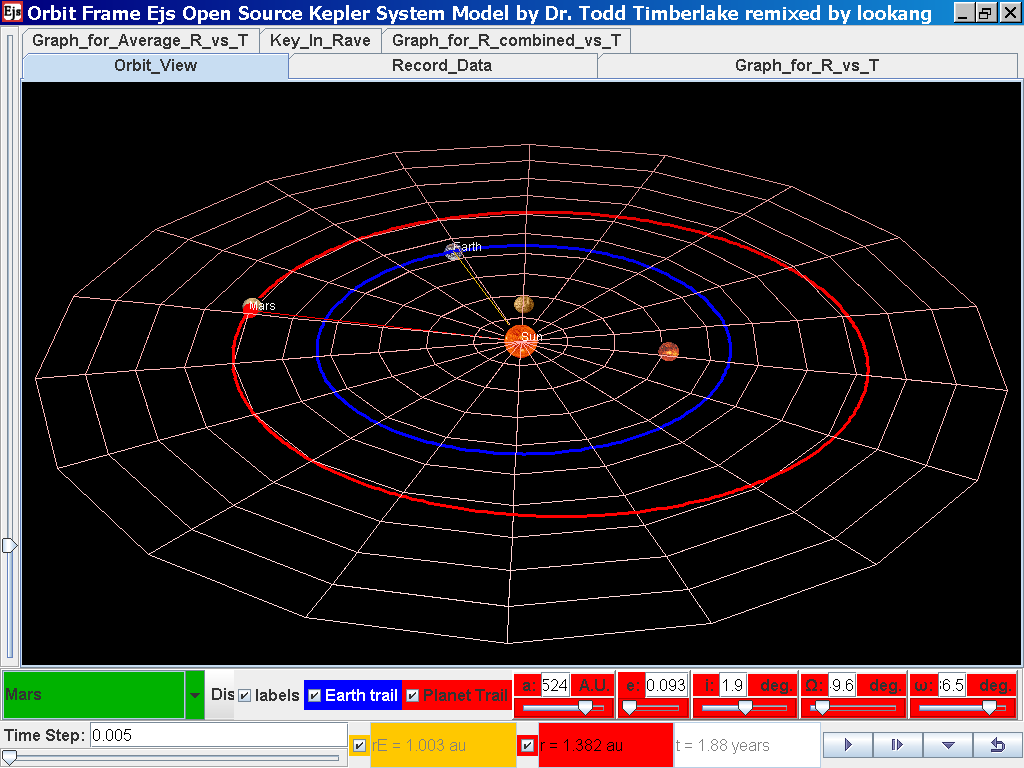
again click on the next tab Record_Data and select Record_Data.
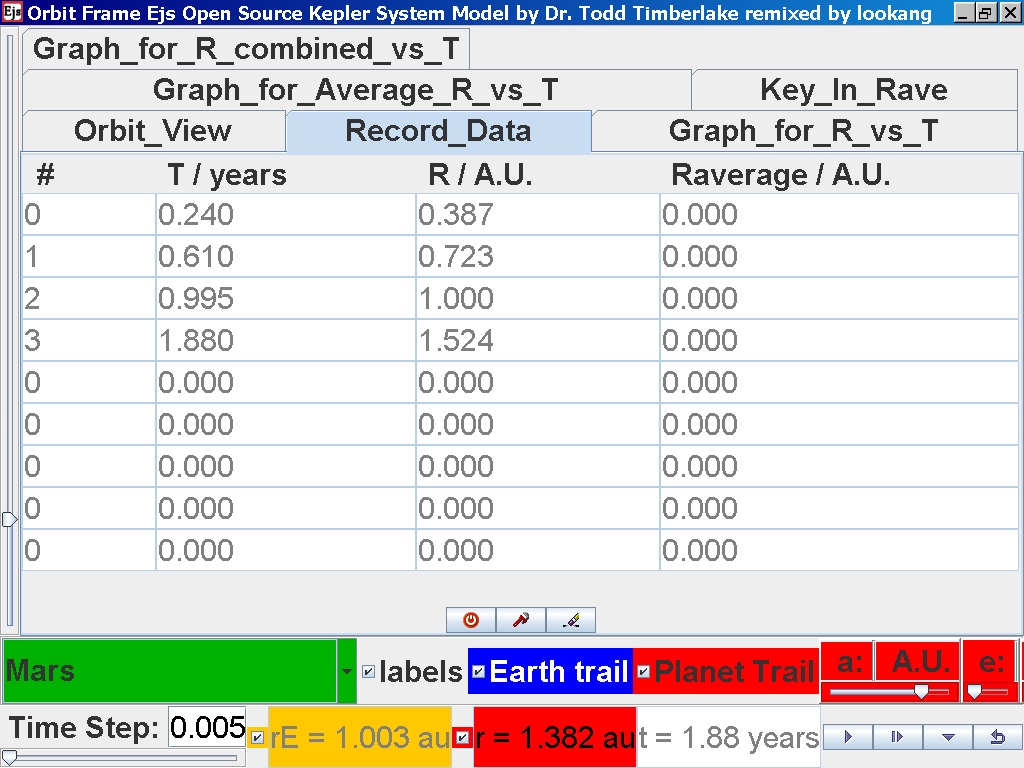
Click back to the Orbit_View and to go to the next planet to collect data,
select from the drop down menu again and select the next planet say Jupiter.
Play the simulation for one complete cycle and increase the time step =
0.08 years reduces the time needed to wait for one cycle.
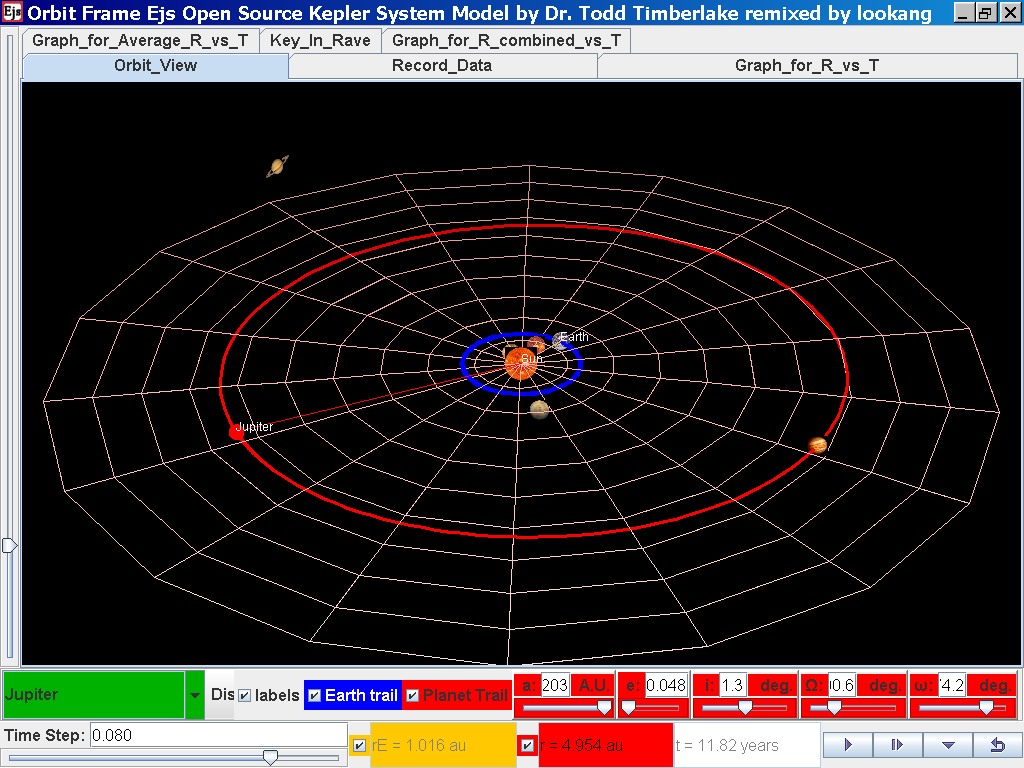
again click on the next tab Record_Data and select Record_Data.
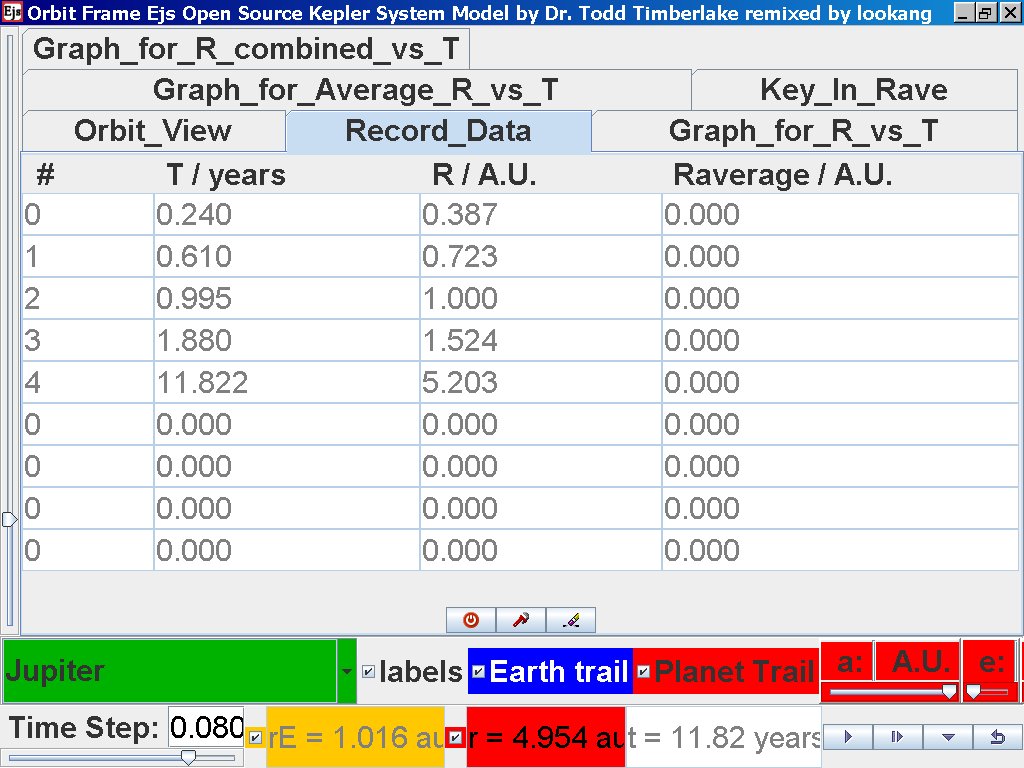
Click back to the Orbit_View and to go to the next planet to collect data,
select from the drop down menu again and select the next planet say Saturn.
Play the simulation for one complete cycle
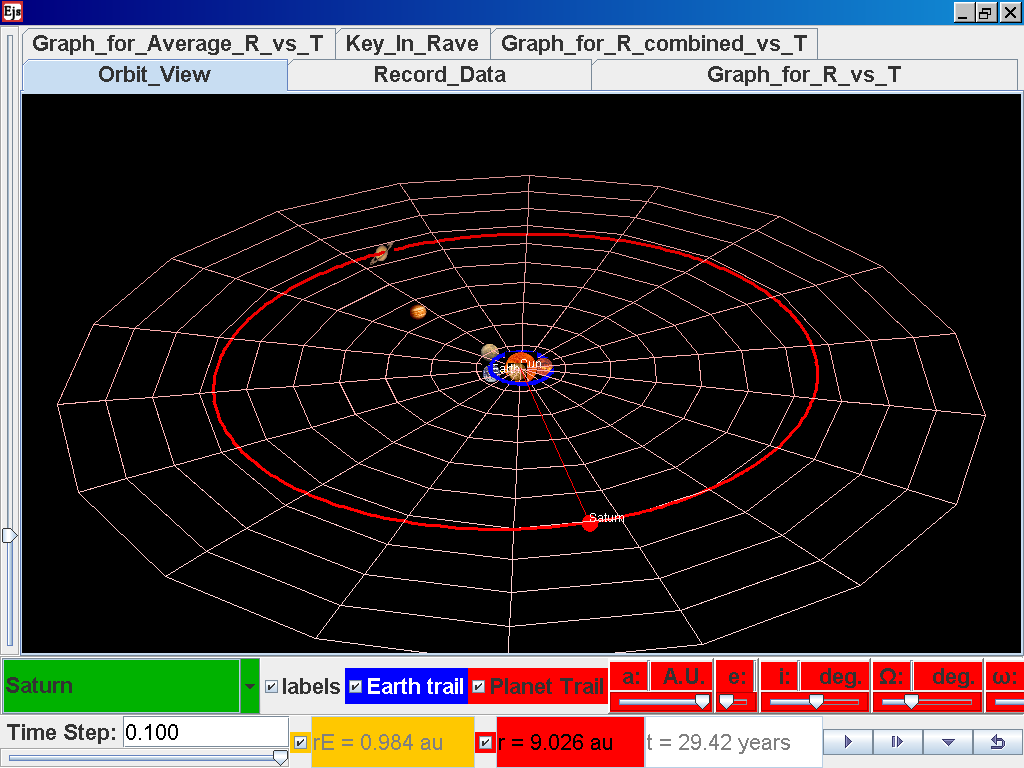
again click on the next tab Record_Data and select Record_Data.
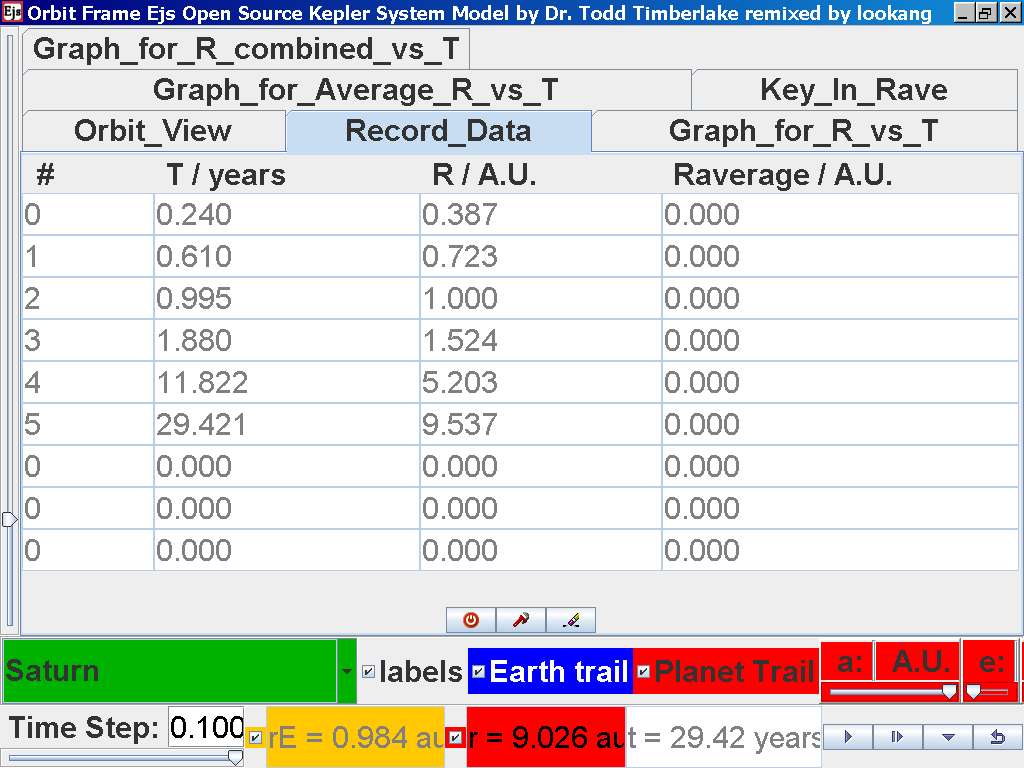
Click back to the Orbit_View and to go to the next planet to collect data,
select from the drop down menu again and select the next planet say Uranus.
Play the simulation for one complete cycle
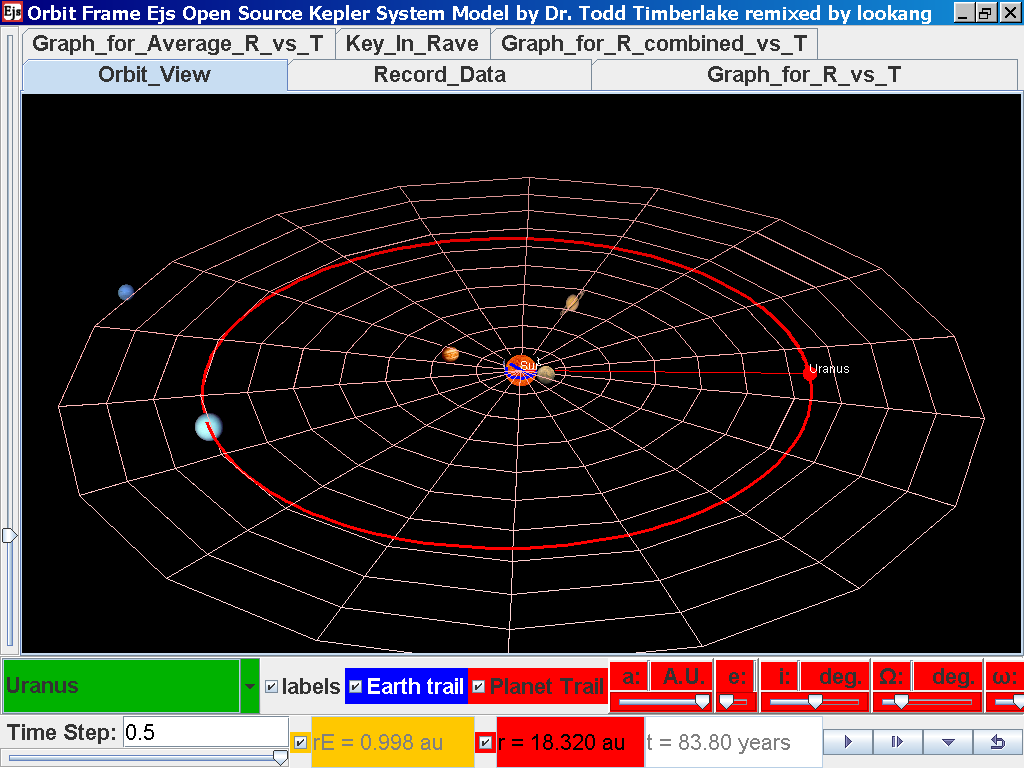
again click on the next tab Record_Data and select Record_Data.
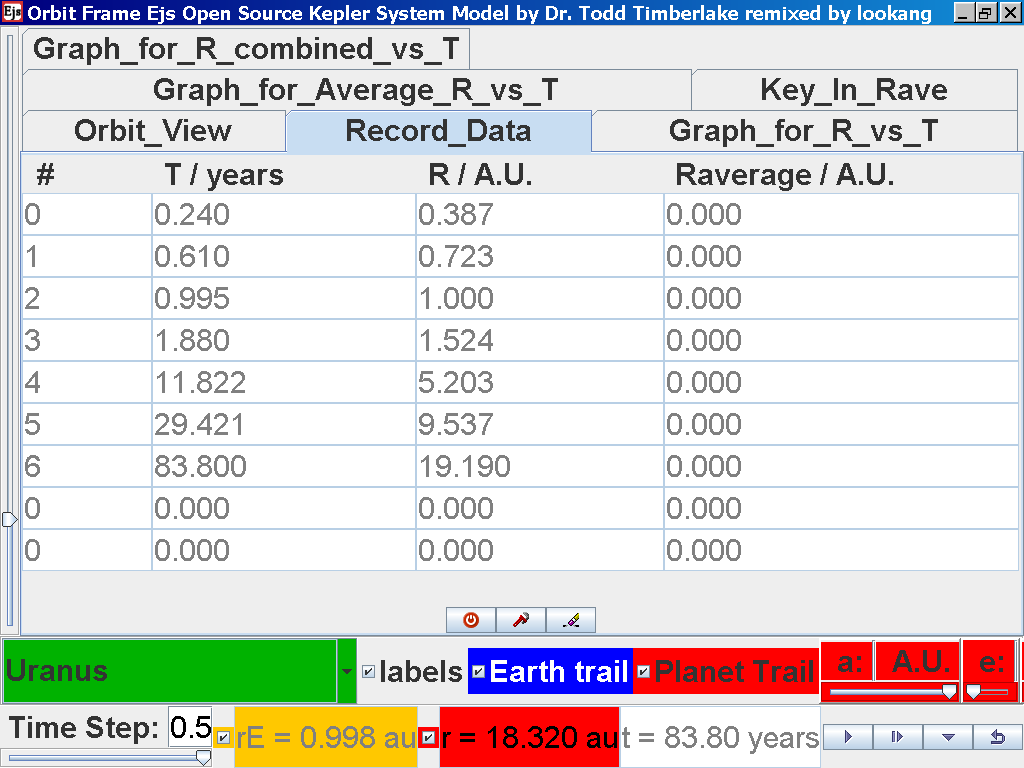
Click back to the Orbit_View and to go to the next planet to collect data,
select from the drop down menu again and select the next planet say Neptune.
Play the simulation for one complete cycle
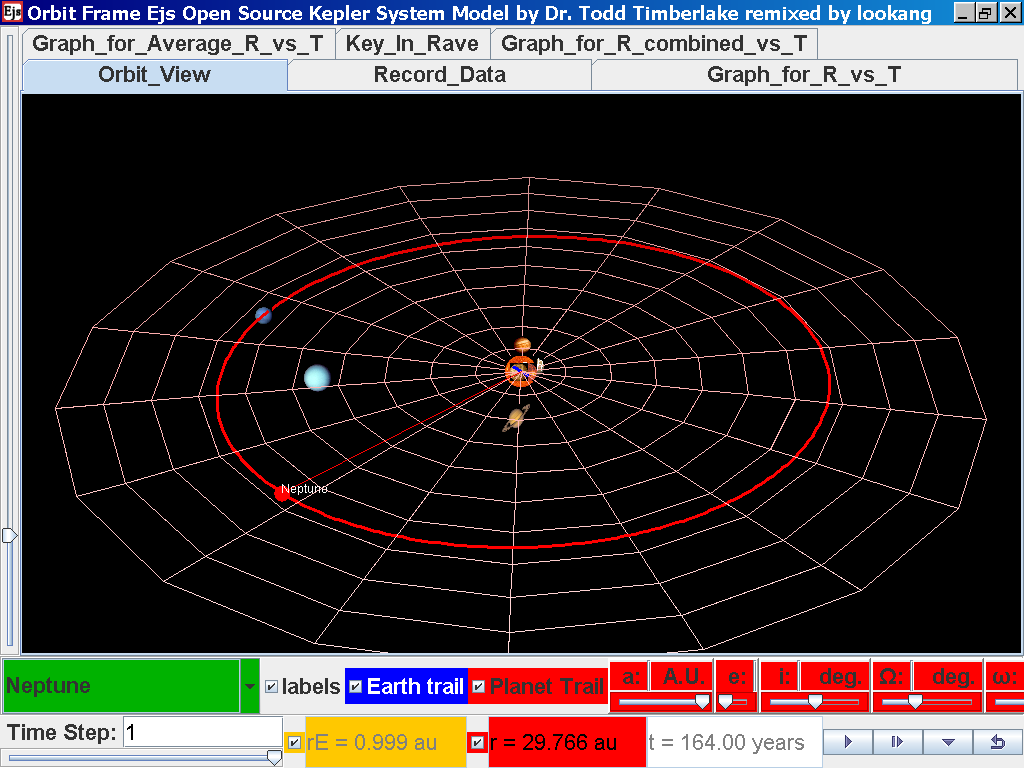
again click on the next tab Record_Data and select Record_Data.
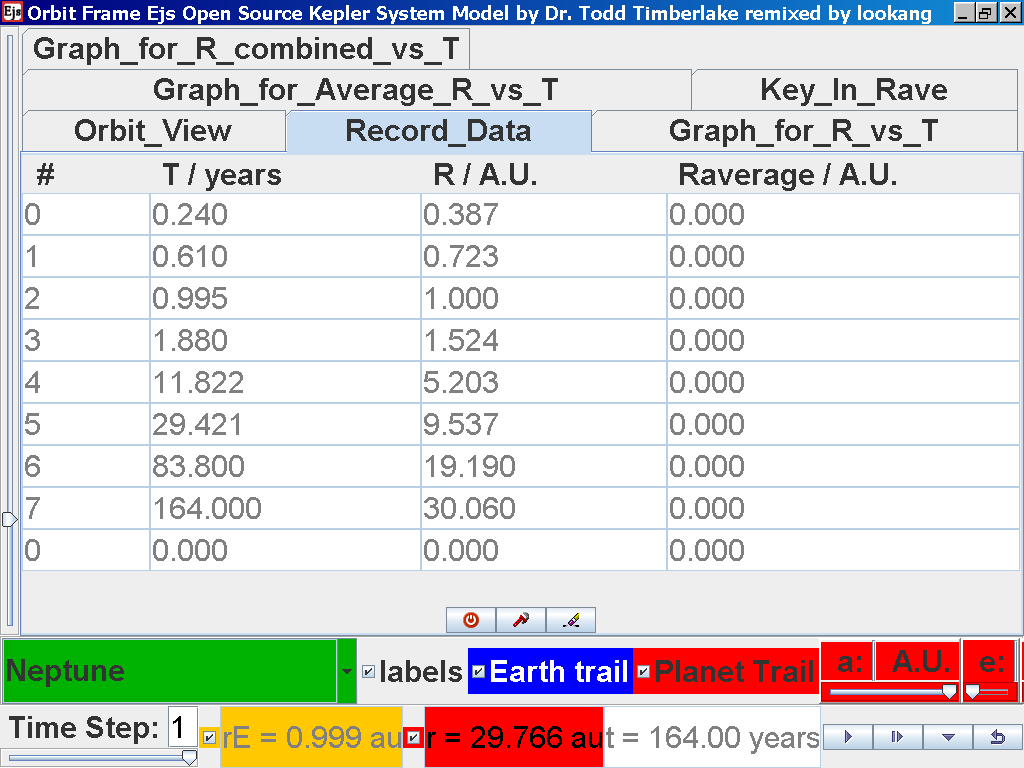
Click back to the Orbit_View and to go to the next planet to collect data,
select from the drop down menu again and select the next planet say Pluto.
Play the simulation for one complete cycle
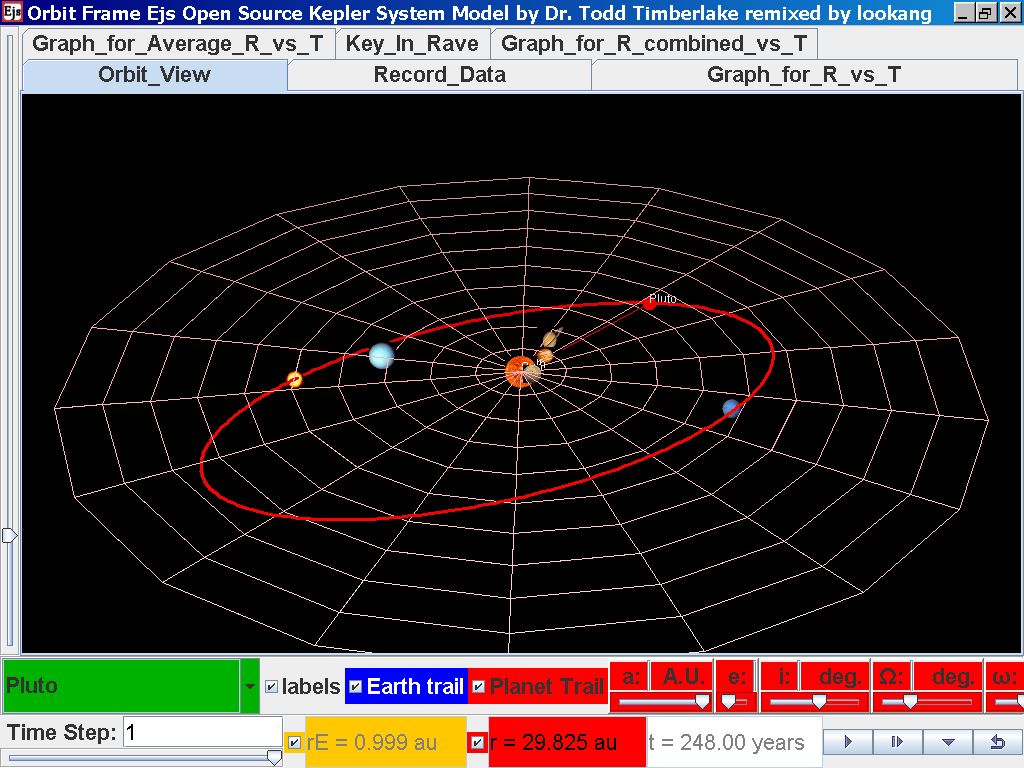
again click on the next tab Record_Data and select Record_Data.
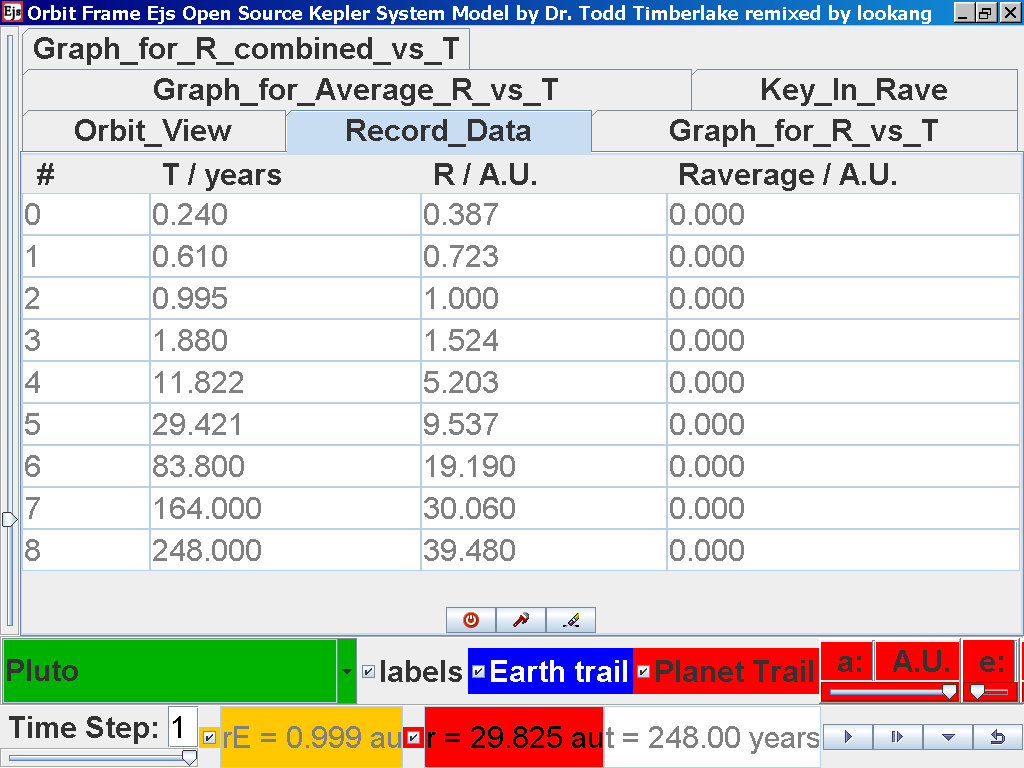
Notice all the data on the actual T /years recorded by you is slightly
different and the mean radius of orbits R / A.U. astronomical units which 1
A.U. = mean distance of Earth to Sun.
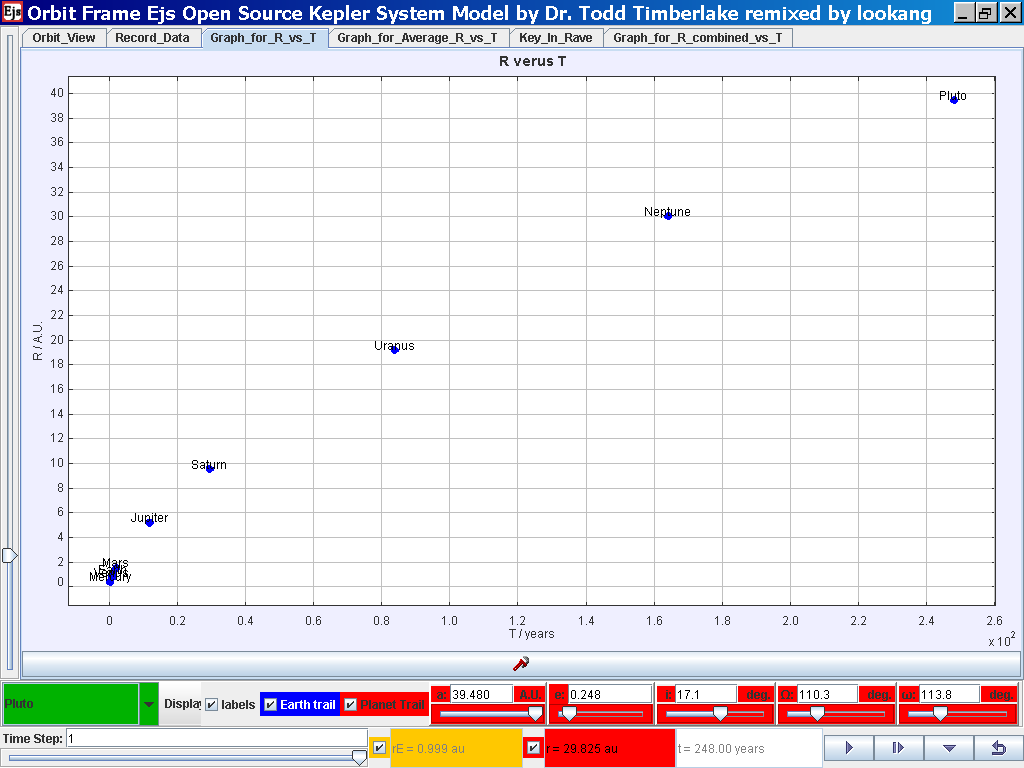
Select the tab Graph_for_R_vs_T and the simulation automatically plots the
data.
Click on the Data Analysis Tool to bring up the following pop up view for
further trend fitting.
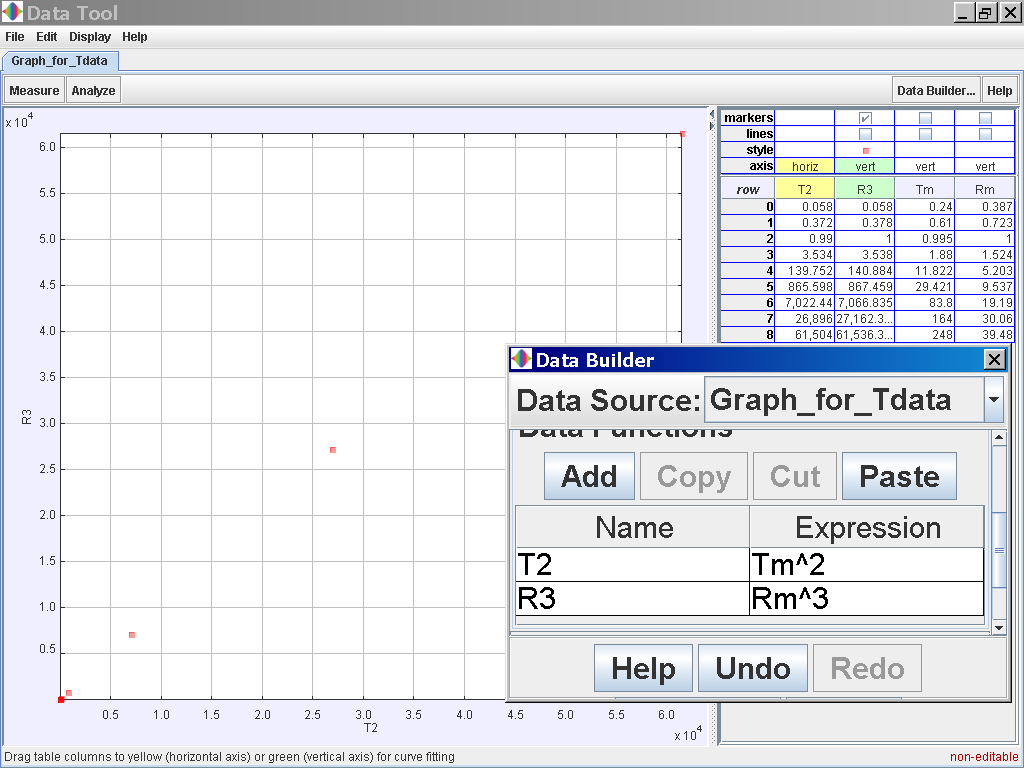
Select the Data Builder Button at the top right corner
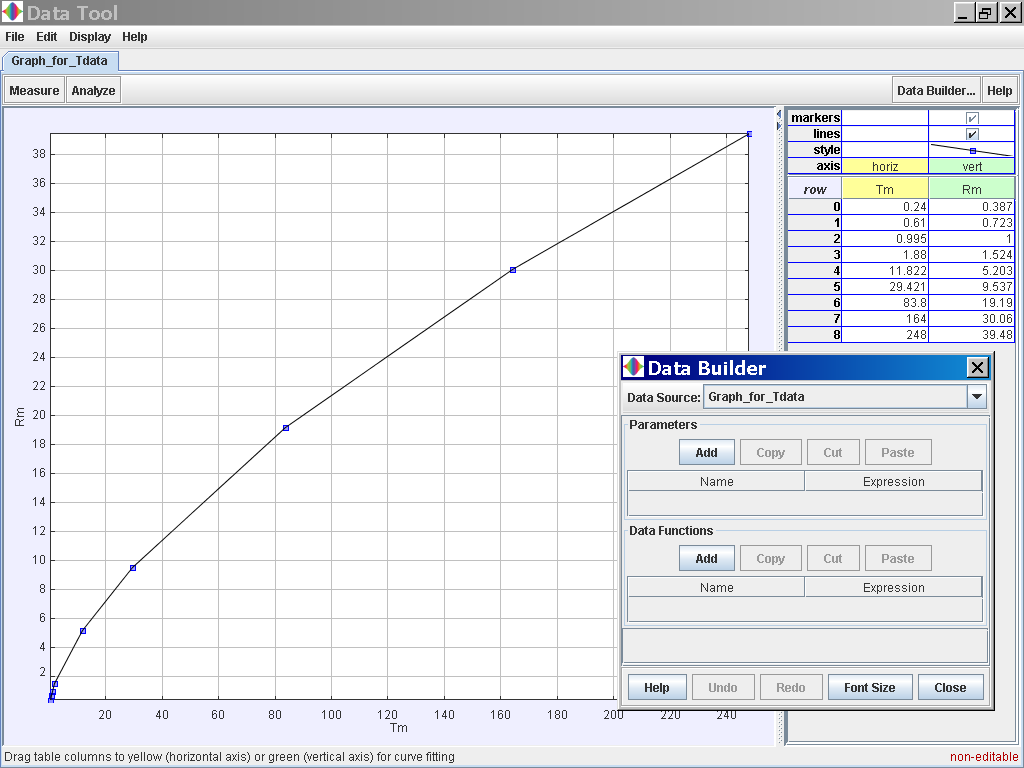
Click on the Data Function Add button to add your own functions such as T2
for Tmean2 and r3 for rmean3.
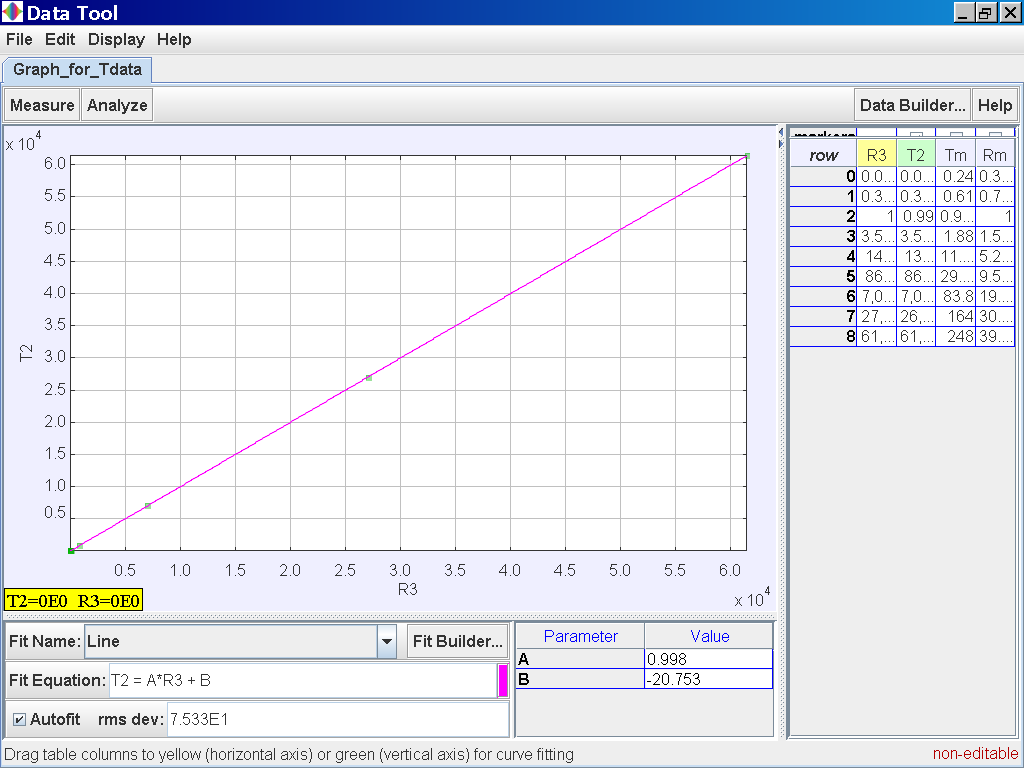
Click on the Analyse
button on the top left corner and select the Linear Fit option of which the
data of T2 and R3 is related by the following line fit
T2 = 0.998 R3 -20.753 which suggests T2 α
r3
Alternative activity, you can also try to log (T) versus log (R)
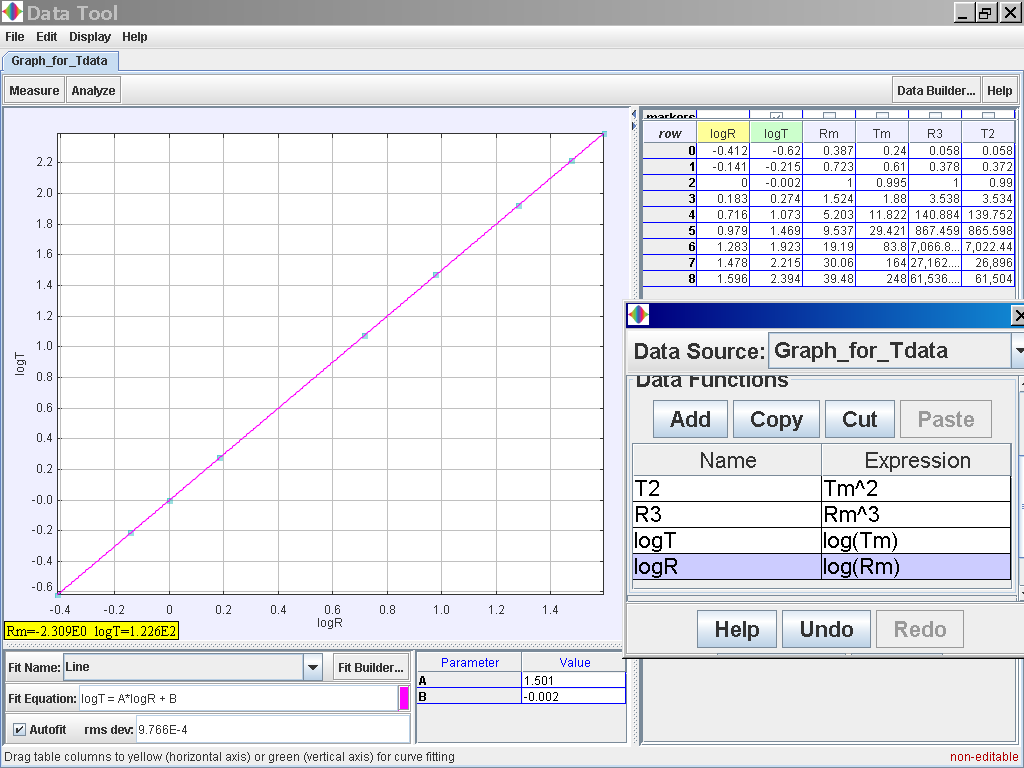notice again log (T) =
1.501 log (R) -0.002 which suggests the same relationship of T α r1.5
or simply T2 α r3
Youtube
https://youtu.be/jt88koyZQuw
Java Model
http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejs/ejs_model_KeplerSystem3rdLaw09.jar