EJSS Earth and Moon Model

EJSS Earth and Moon Model by paco remixed by lookang.

h ttp://weelookang.blogspot.sg/2013/12/ejss-earth-and-moon-model.html
https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_EarthAndMoon3Dwee/EarthAndMoon3Dwee_Simulation.html
source: https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_src_EarthAndMoon3Dwee.zip

https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_EarthAndMoon3Dwee/EarthAndMoon3Dwee_Simulation.html

Description:

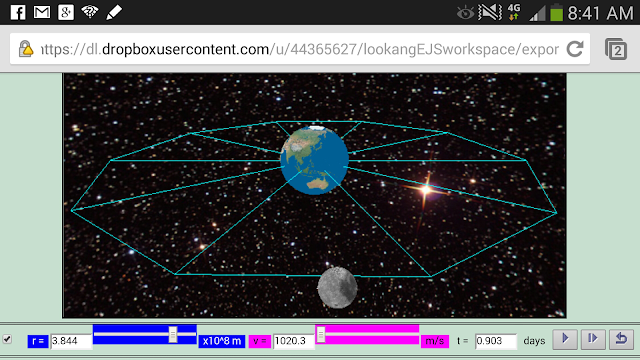
The Moon completes its orbit around the Earth in approximately 27.32 days (a sidereal month). In this model, we assume the Moon to orbit about the center of the Earth. By this assumption, the Moon is at a distance of about 385000 km from the center of the Earth, which corresponds to about 60 Earth radii. With a mean orbital velocity of 1.023 km/s,[1] The Moon orbit is modeled to be a perfect circular motion orbit, a close approximation the real Moon's orbit. The model also assume the Moon to move on the Earth's equatorial plane.

The equations of motion are:

δxδt=vx

δyδt=vy

δzδt=vz

δvxδt=−GMx(x2+y2+z2)1.5

δvyδt=−GMy(x2+y2+z2)1.5

δvzδt=−GMz(x2+y2+z2)1.5

The equations of rotation are:

rotationearth=rotationearth+1δt

rotationmoon=rotationmoon+1360δt

Equations used to calculate physics quantities are:

r=x2+y2+z2−−−−−−−−−−√

v=v2x+v2y+v2z−−−−−−−−−−√

theta=tan−1yx

The model used

δt=1, the time taken for Earth to rotate i complete revolution is therefore

tday=t360

so after 360

δt steps,

tday=1

To calculate period T,

omega=vr

therefore,

T=2πω

For collision detection, i used

r<rEarth+rMoon

For largely visualization purposes,

rEarth=0.637 some what familiar to real data

rMoon=0.1737 not to scale

in order to create realistic simulation, the model used constants to create numeric that corresponds to the real world.

for example in the model versus in the world,

MEarth=0.6=6x1024kg

G=0.667k=6.67x10−11m3kg−1s−2

where

k=0.58x10−4 to achieve comparable period

T=27.3 days

r=3.844=385000km

and velocity of moon is

vcal=(v)(1x109)k1 where

k1=2.4 arbitrarily determined

changes made:

added realistic numbers in the model

added better graphics from creative commons or public domain pictures

added plane of Moon's rotational plane

added control and sliders to suit my usual design ideas

Activities:

set the velocity to zero and play the simulation, is it as you expected it to observe? What is the physics concepts that can be used to explain this?