Satellite in Circular Orbits

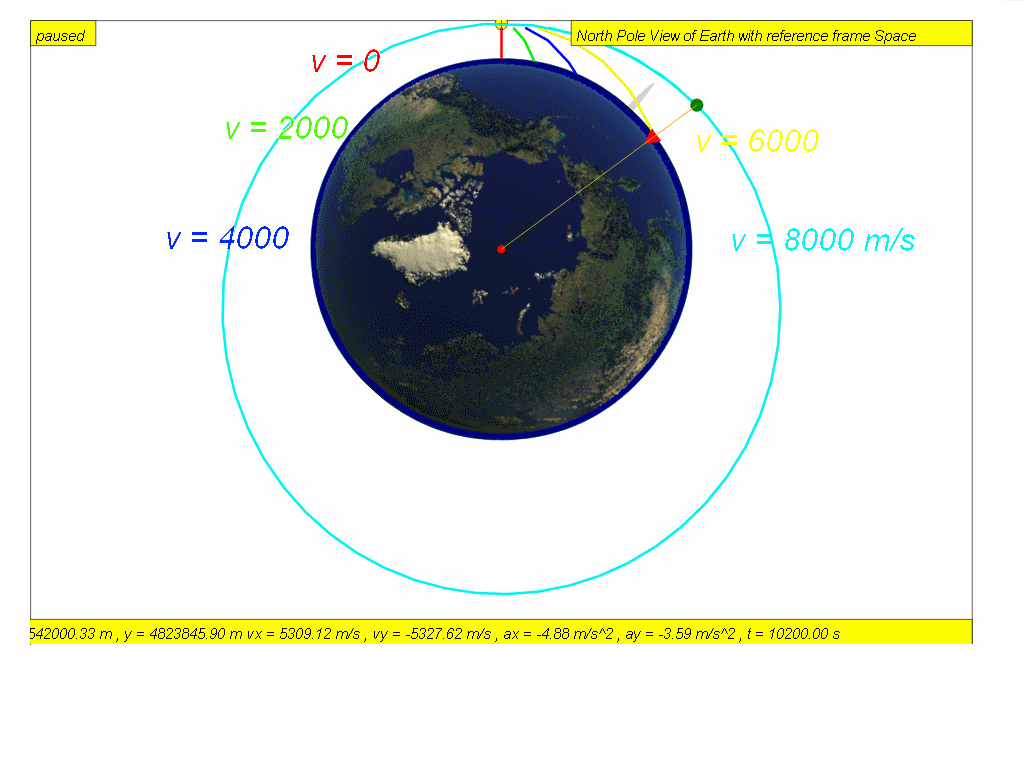
An object projected horizontally near the Earth’s surface follows a parabolic trajectories as shown ( v = 0 red, v = 2000 green, v = 4000 blue, v = 6000 yellow and v = 8000 teal) .

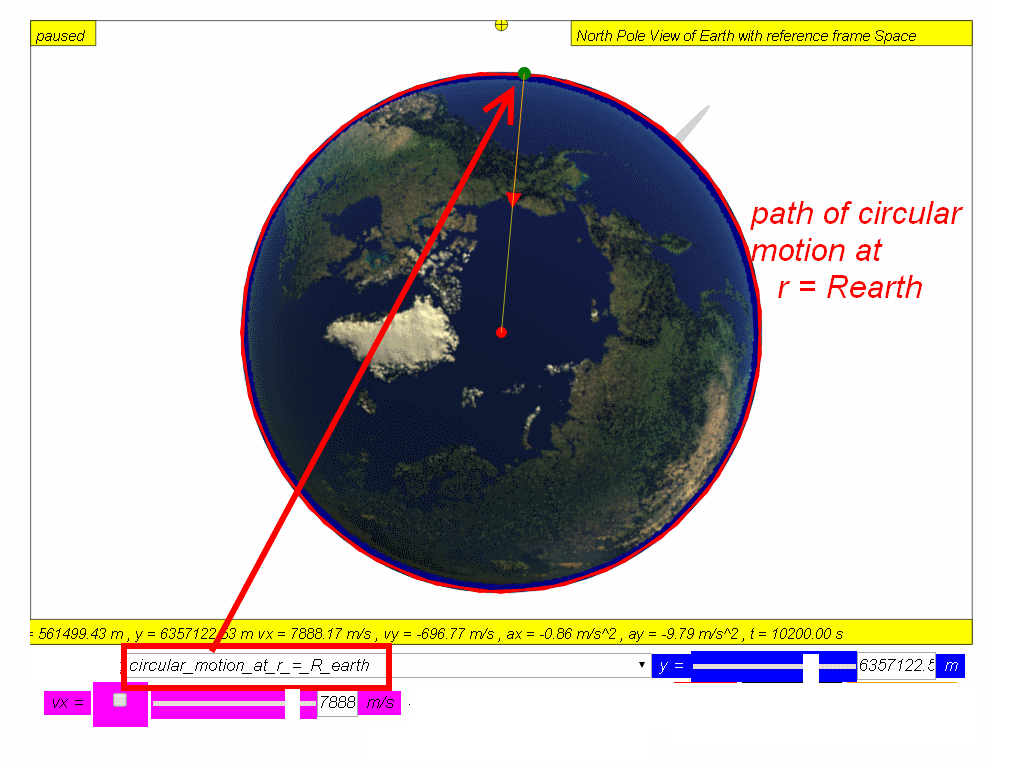
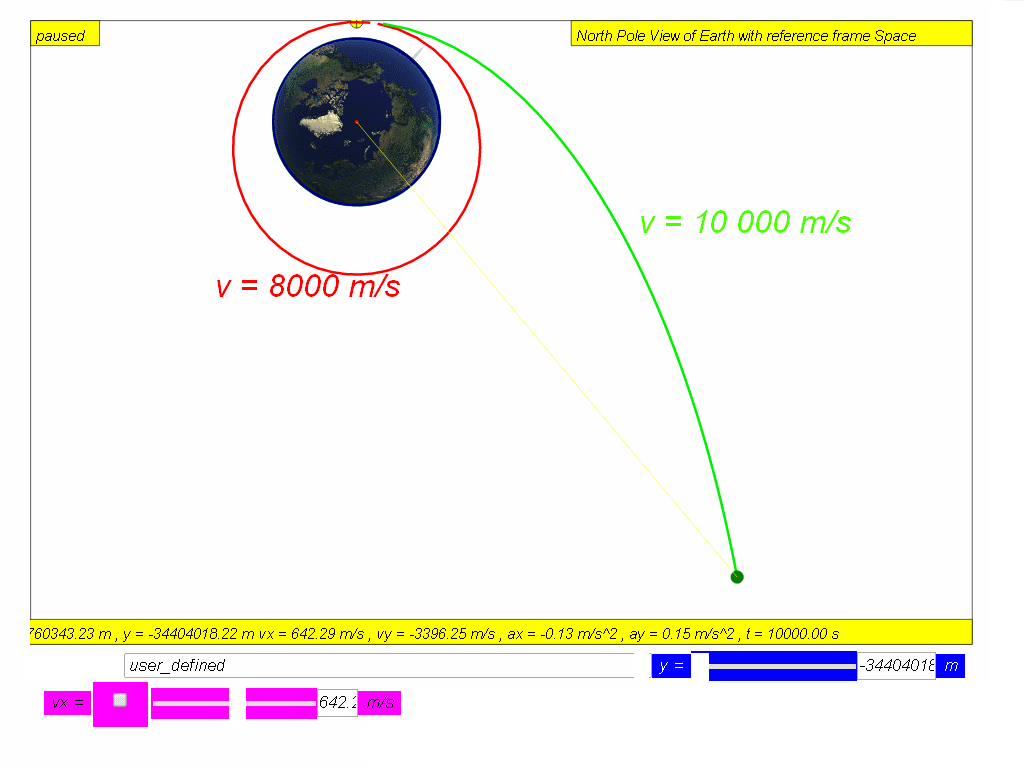
As the speed of projection v increases, the object will reach a speed approximately v = 7888 m/s where the trajectory follows the curvature of the Earth’s surface.

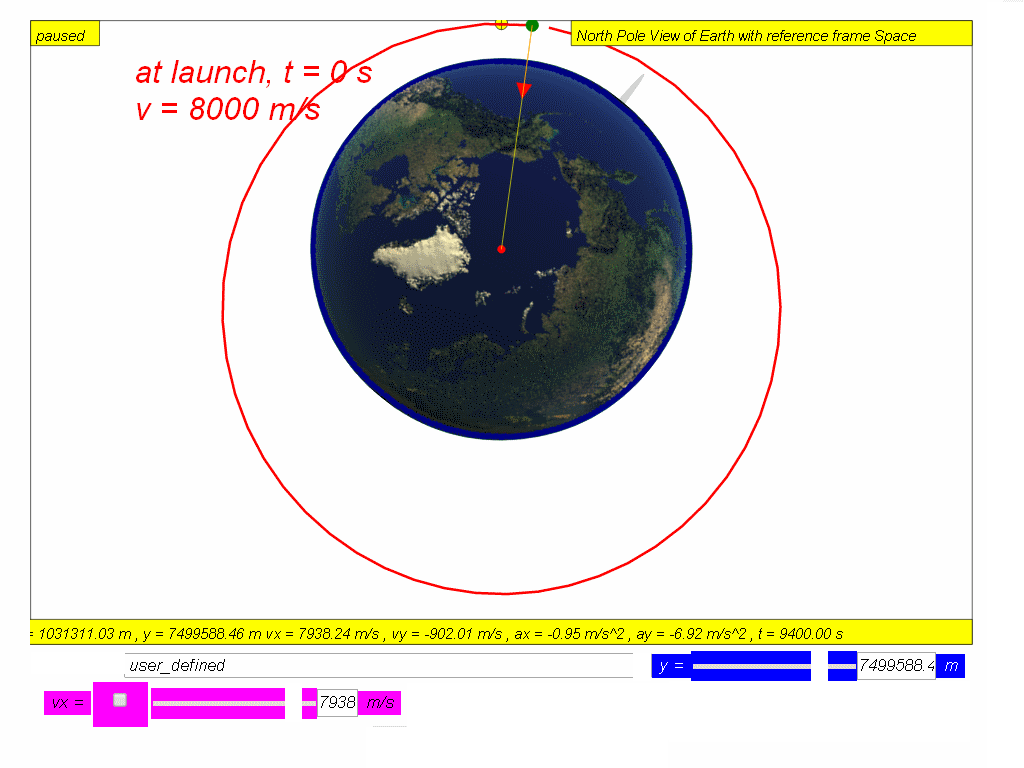
If air resistance is negligible, the object will orbit round the Earth continuously and will never meet the Earth’s surface such as speed v 8000  red m/s and v = 10000 m/s green.

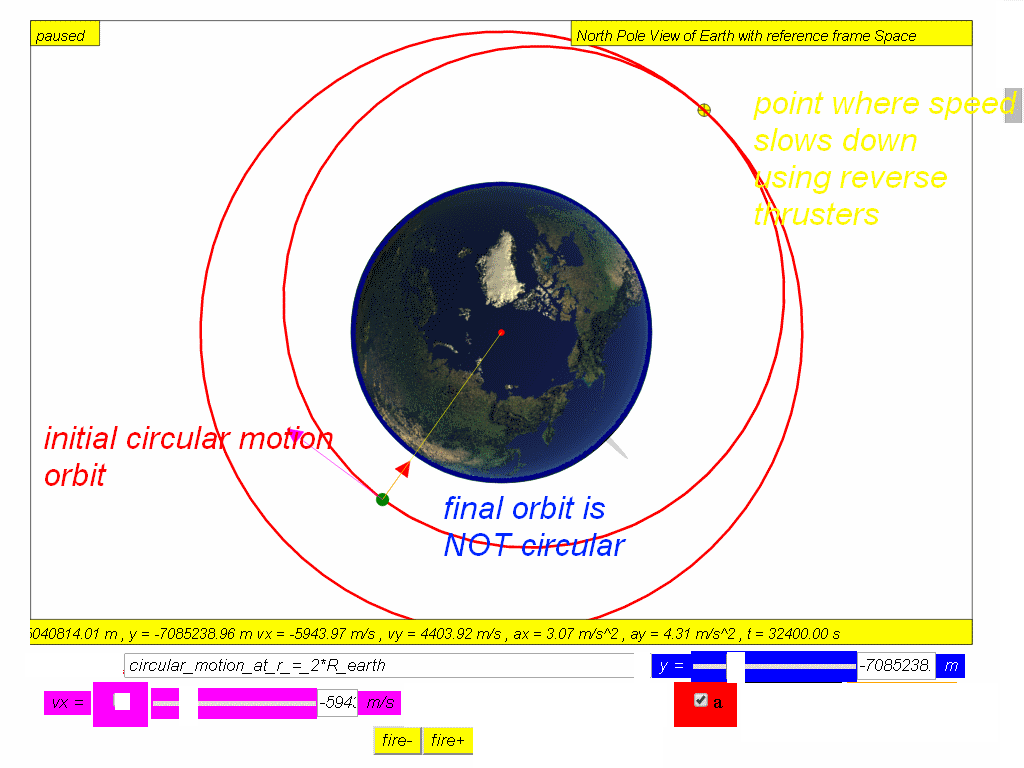
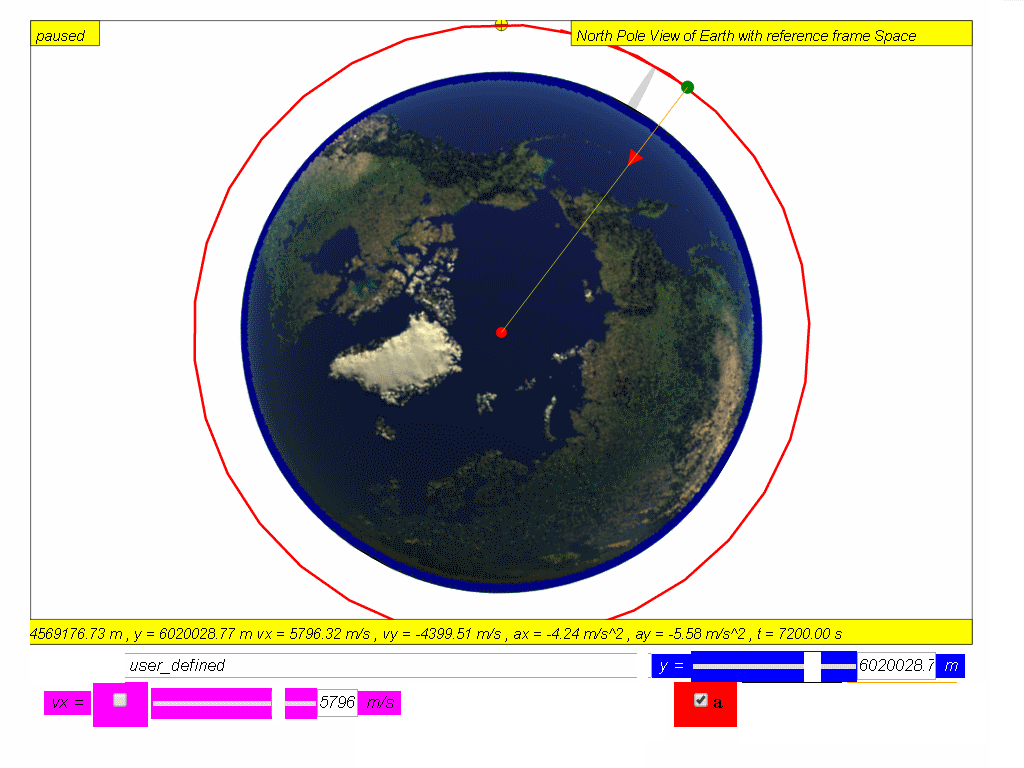
Many man-made satellites move in circular orbits around the Earth. The first man-made satellite, the “Sputnik 1”, was launched by Soviet Union in 1957. Since then, hundreds of satellites have been launched into orbit around the Earth. The only force acting on the satellite in a circular orbit (achieved by launching horizontally at vx =7276.69 m/s at height above Earth surface  H = 0.185 R_E where R_E = 6370 000 m is the radius of Earth,  is the Earth’s gravitational force. The gravitational force (red arrow is directed towards the centre of Earth) is also the the centre of the circular orbit.

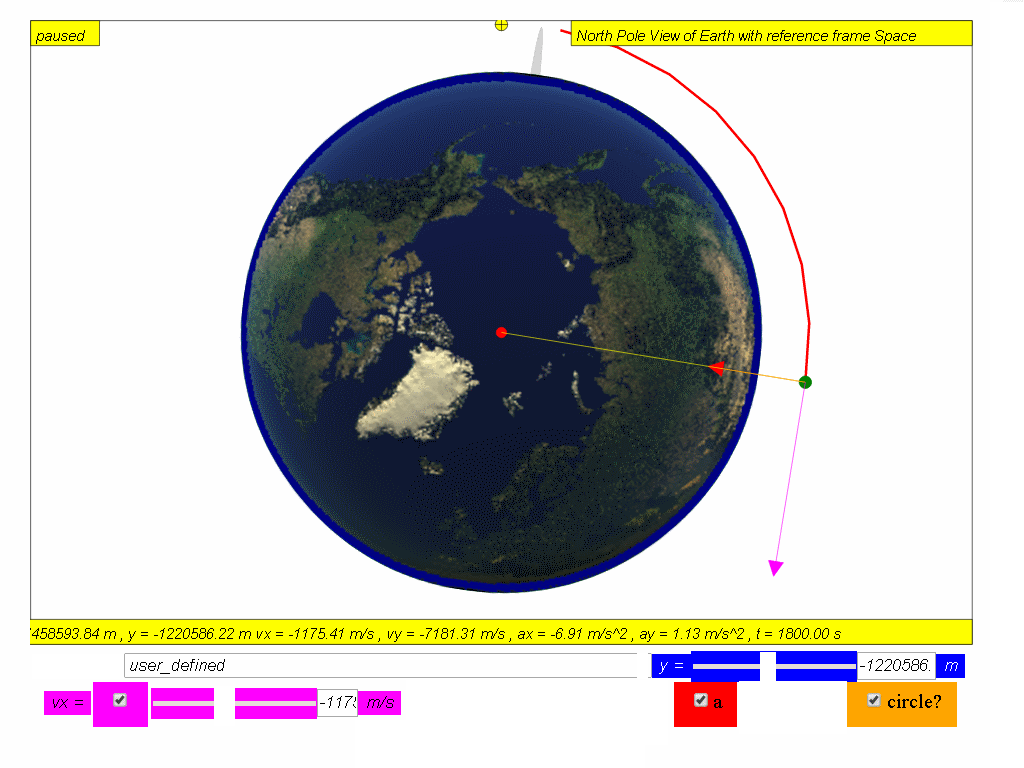
Since the satellite velocity (magenta arrow)  is perpendicular to the gravitational force (Red arrow), its magnitude of velocity remains constant while its direction changes. 

This means that the satellite is traveling in a uniform circular motion (recap Topic 6).  At the same time, the distance from the satellite to the centre of Earth will also remain constant in this circular orbit.

For a satellite (or any object) in circular orbit, the gravitational force acting on it is the centripetal force that keeps it in circular motion.

Using newton's second law in this context of a circular motion orbit.

$F$ = m v 2 r

since in outer space, the assumption is only Earth's gravitational field is responsible for the circular motion and gravitational force is $F$ = G m M r 2

thus, $\genfrac{}{}{0.1ex}{}{G}{}$ m M r 2 = m v 2 r

the expression can be simplified to give the exact velocity required for circular motion  $\sqrt{\genfrac{}{}{0.1ex}{}{G}{}}$ M r = v This equation-formula can be used to calculate the speed required for any object to orbit around a planet of mass M at a constant distance-radius of orbit r.

Inquiry:

Suggested Steps to conduct inquiry

1. select from drop-down menu option circular_motion_at_r_=_2*R_earth
2. click play and observe the motion of the orbit. describe the motion is circular or otherwise.
3. pause the simulation
4. click fire- to simulate firing of reverse thrusters for a very short time, to reduce the speed of the object in orbit.
5. observe the motion of the new orbit. describe the motion is circular or otherwise.
6. design an alternative inquiry option and write down briefly what you have found out.
7. discuss with more classmates in the school and suggest an a community of learners what you have concluded from the evidences collected by at least 3 other independent approach/options.

Calculation of speed at r = 3 times Radius of Earth

1. draw a sketch 
2. decide on the symbols and values, r = 4(6.4 x 10⁶) = 2.56x10⁷ m
3. recall the formula and derive from newton's law $\genfrac{}{}{0.1ex}{}{G}{}$ m M r 2 = m v 2 r
4. substitute the values $\genfrac{}{}{0.1ex}{}{6.67}{}$ x 1 0 -11 ( 6.0 x 1 0 24 ) ( 2.56 x 1 0 7 ) 2 = v 2 2.56 x 1 0 7
5. imply 3.94x10³ m/s = v
6. check the answer, put v back to check if $\genfrac{}{}{0.1ex}{}{G}{}$ m M r 2 = m v 2 r still hold for both left and right hand sides of the equal sign.

Java Model

http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejs/ejs_model_NewtonsMountainwee06.jar

Model

https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_gravity08/gravity08_Simulation.xhtml