Gravitational
Field Strength (symbol: g and units: N kg-1 or m s-2)
As seen in earlier section, the gravitational field strength
acting on an object decreases (illustrated by an increase in the
field line spacing) as the object moves further away from Earth.
This means that field strength varies with distance from the
source mass (in this case, the Earth).
The gravitational field strength, g at a particular point in free
space is defined as the gravitational force per unit mass
acting on a point mass placed at that point.
Inquiry:
Why must it be
a “point mass”?
Point mass is physically small so that the forces acting on
different parts of the point mass are generally the same.
LO(c)
Based on
Newton’s law of gravitation, the gravitational force acting on the
point mass, m by the source mass, M,
and
gravitational field strength, g is the gravitational force, F per
unit mass acting on the point mass, m, we may derive that the
gravitational field strength.
since we know
the force on object as a result of the gravitational field created
by Earth is F = mg.
putting the 2
equations together, we get
let Earth be M = M1, assuming mass of object is m = M2,the equation can be simplified
giving us the expression for
gravitational field field g
Note:
the following shows the different g
field strength at different positions away from the mass M
creating the gravity field strength g.
From left to right,
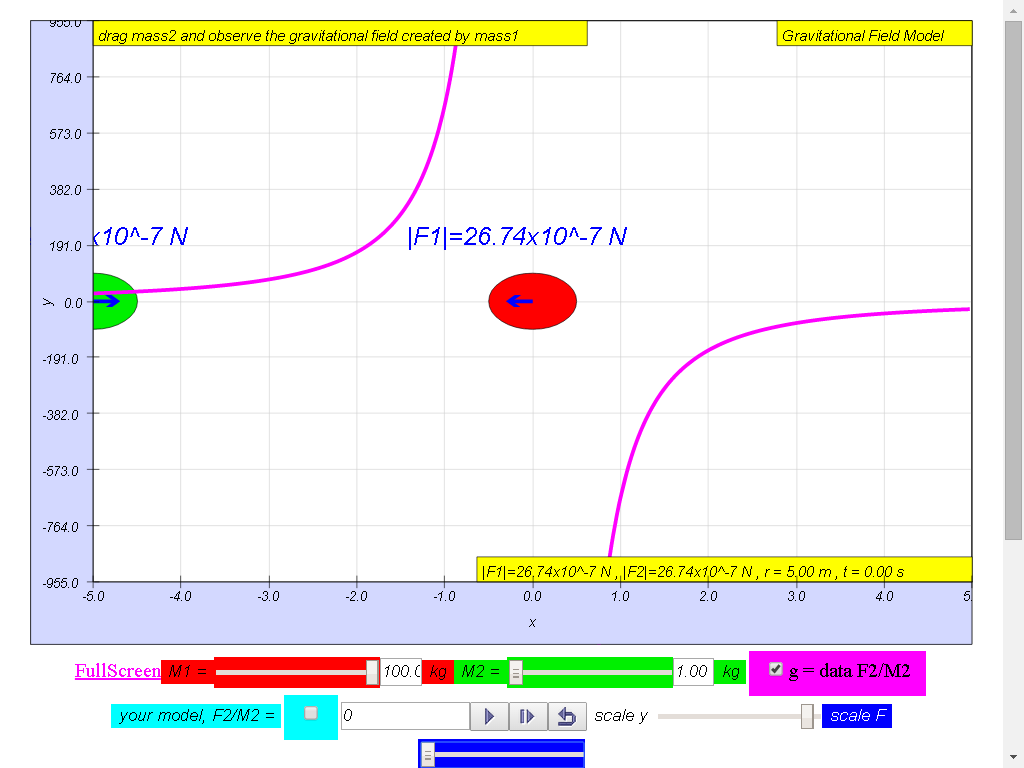
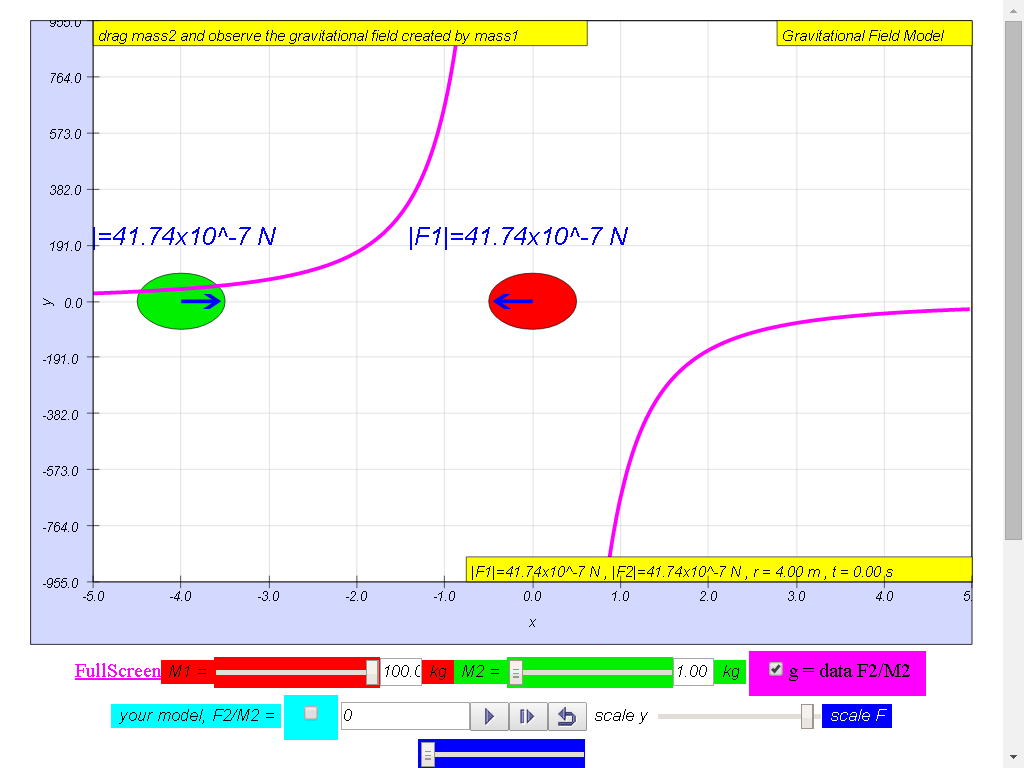
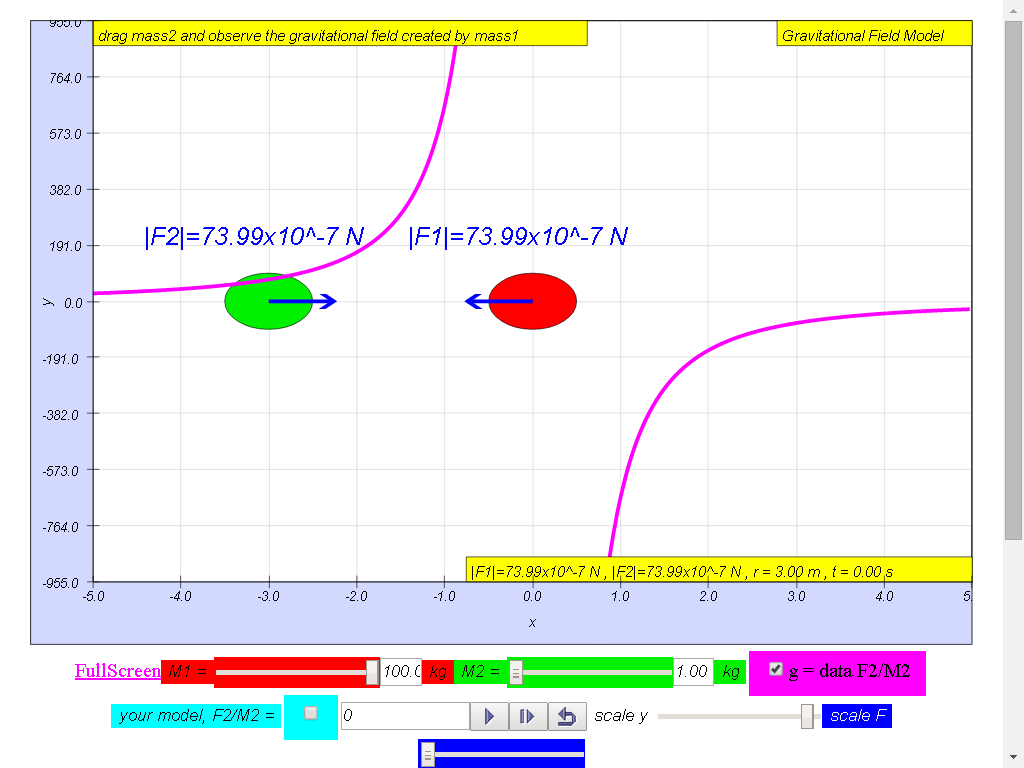
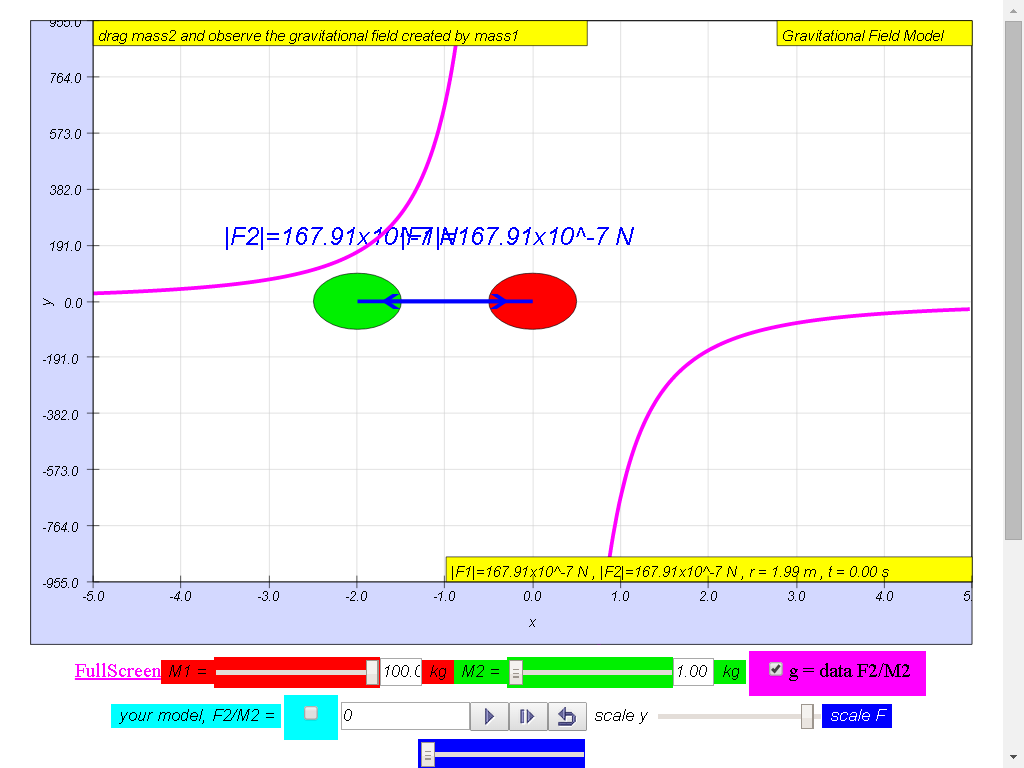
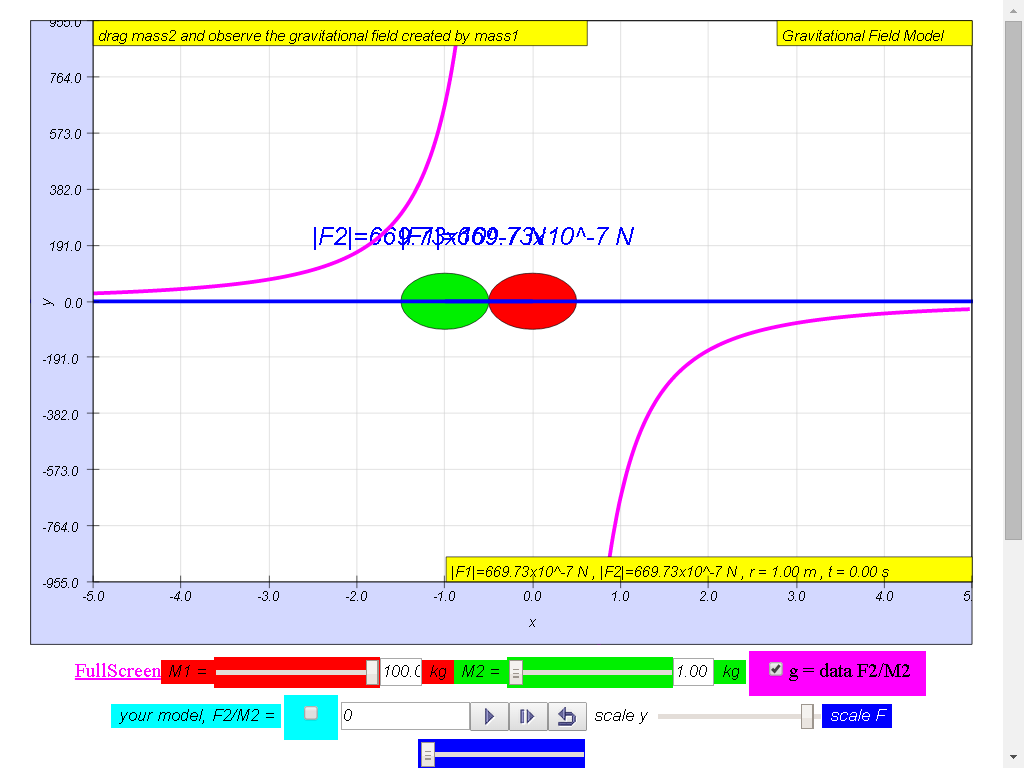
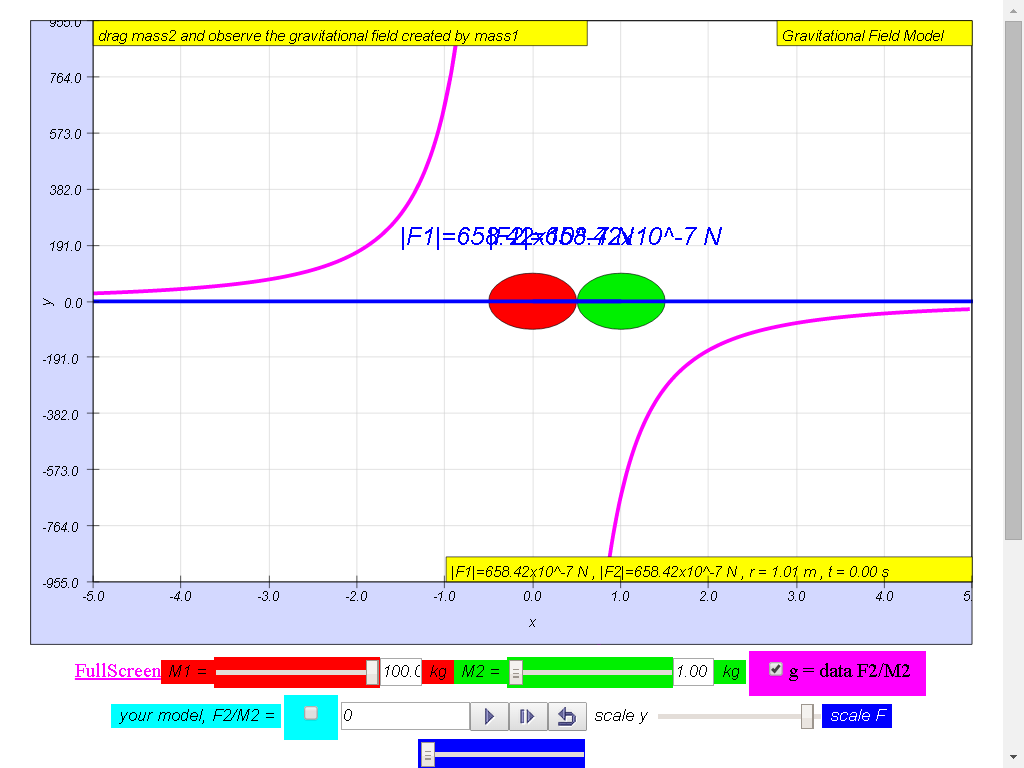
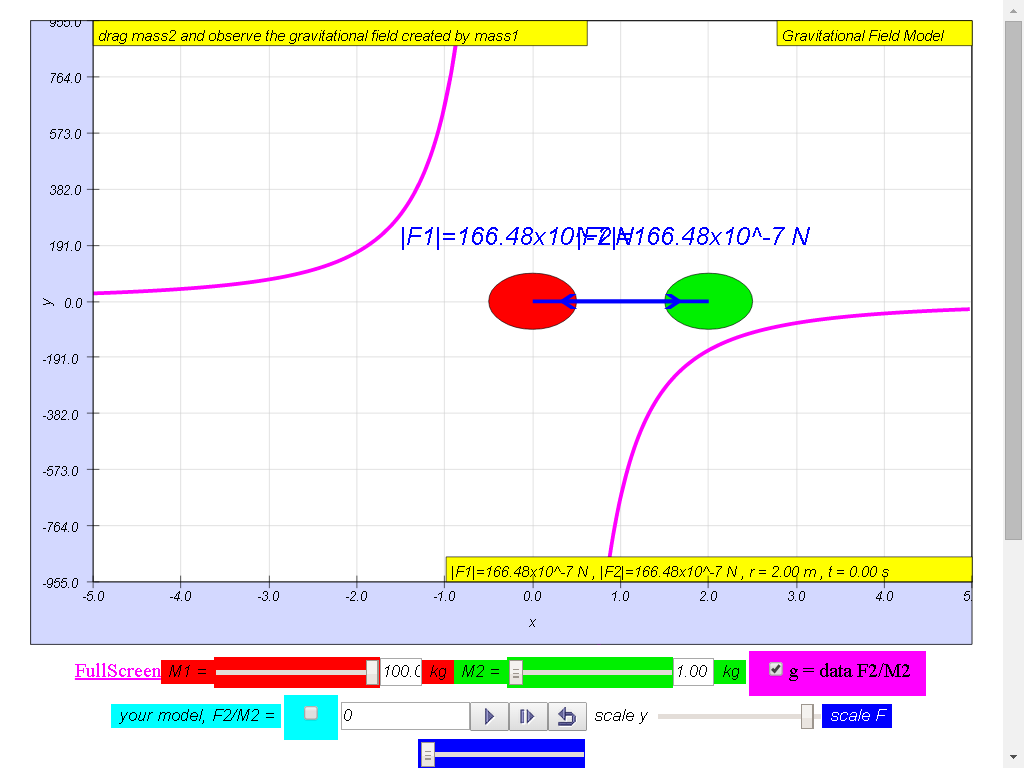
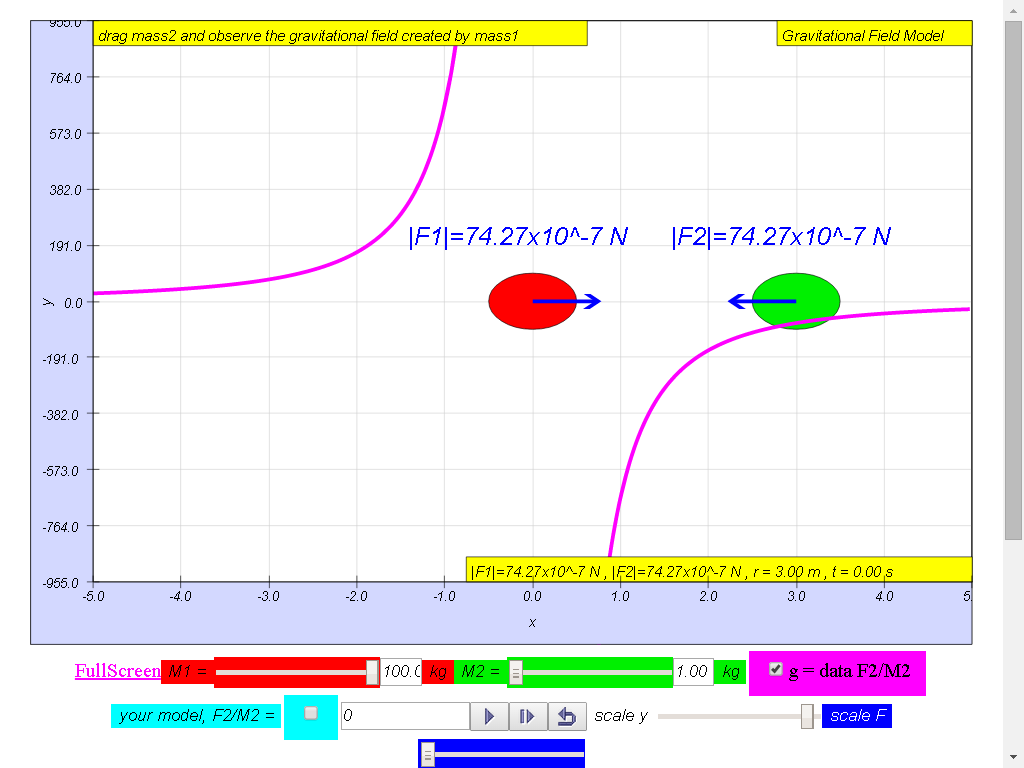
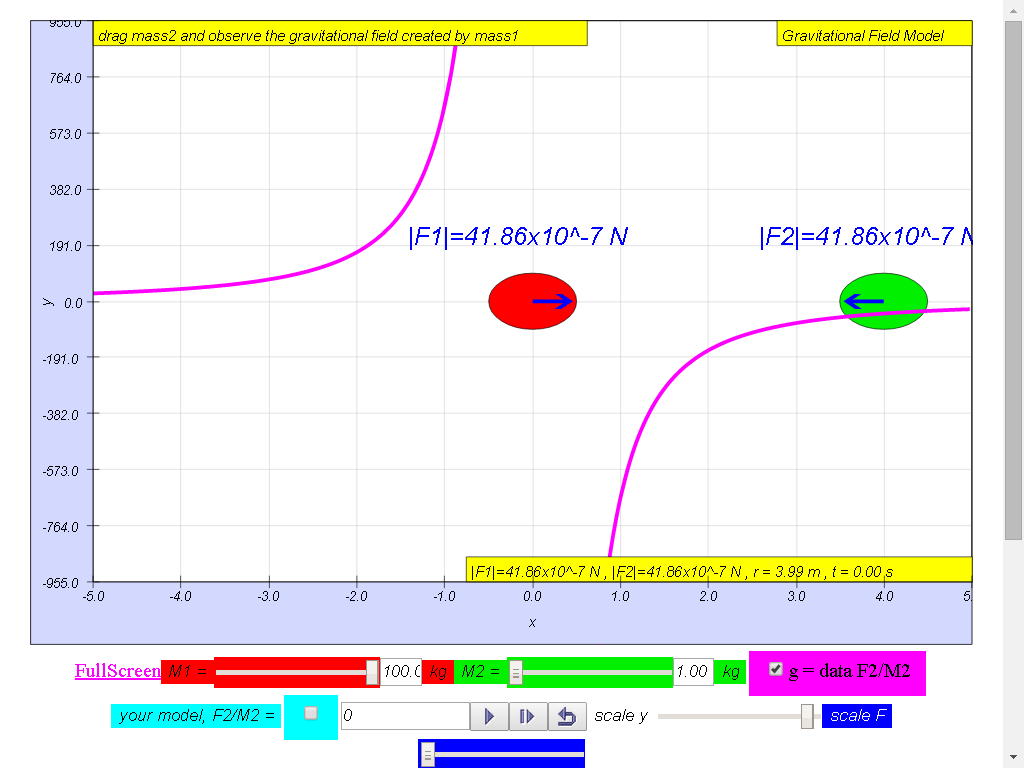
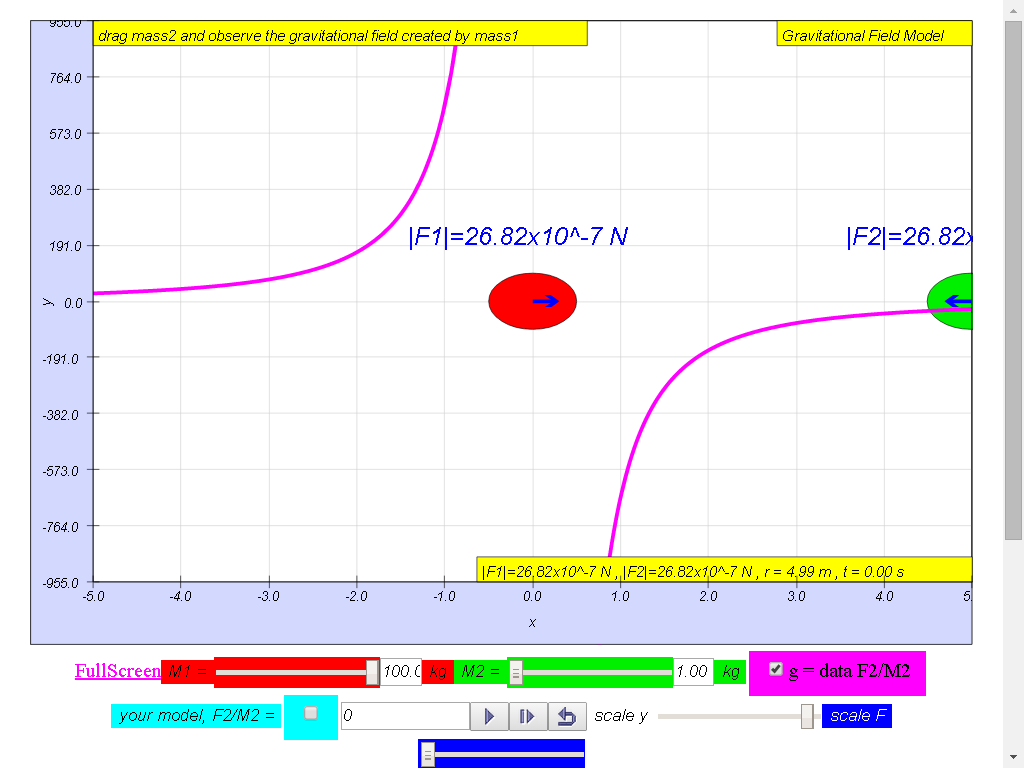
Notice the values of g changes direction
left (negative) to right (positive), suggest whether g field is a
vector (magnitude and direction) or scalar (only magnitude, no
direction) quality.
1) Gravitational field
strength, g (depicted as a magenta color curve) is a vector
quantity, and it has the direction always towards the mass M.
Try varying the values of the green test
mass m, does it change the value of g?
2) As shown in , the gravitational field strength of
source mass M , g is independent of the mass at that point,
m.
As depicting in the pictures above, the
values of g changes according to what relationship? linear,
quadratic, inverse square etc?
try your own model by keying expression
to test linear = "r", quadratic = "r^2", inverse square =
"1/r^2". which model seems to depict the g well enough?
3) The magnitude of
the field strength , g varies according to the in inverse square
law manner .Hence gravitational field is also known
as an inverse square law field.
4) All the picture are
showing the (depicted as a magenta color curve) g vs r graph for a
100-kg mass :
• On the left side of
the 100-kg mass, the gravitational field strength points to the
right are positive g values.
• On the right side of
the 100-kg mass, the gravitational field strength points to the
left are negative g values. the reason is because of the adoption
of the Cartesian coordinate system with positive x direction to
the right.
• As r increases,
magnitude of g decreases according the formula
Youtube
https://youtu.be/nZSHpQmlddk
Java
Model
http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejs/ejs_model_GField_and_Potential_1D_v8wee.jar
Model:
use the model field to propose a
mathematically valid equation to represent the gravitational field
strength, g.
hint: try typing in expression
like 6.67*100/r^2 (left) and - 6.67*100/r^2 (right)
separately.
note that the model field assumes G =
6.67 instead of 6.67x10-11. , M = 100 kg, r is the distance away
from M (red gravitational field source mass)
https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_gravity04/gravity04_Simulation.xhtml









