Example
of Application of potential φ
Revision: The total φ at a point in a field due to two or
more source masses is the scalar addition of the individual φ due
to each mass at that point, i.e. .
φtotal =
∑ϕ
similarly,
since PE = U = mφ
PE total =
Showing how
the gravitational potential varies between the surface of the Moon
and the surface of the Earth along the line joining the centres.
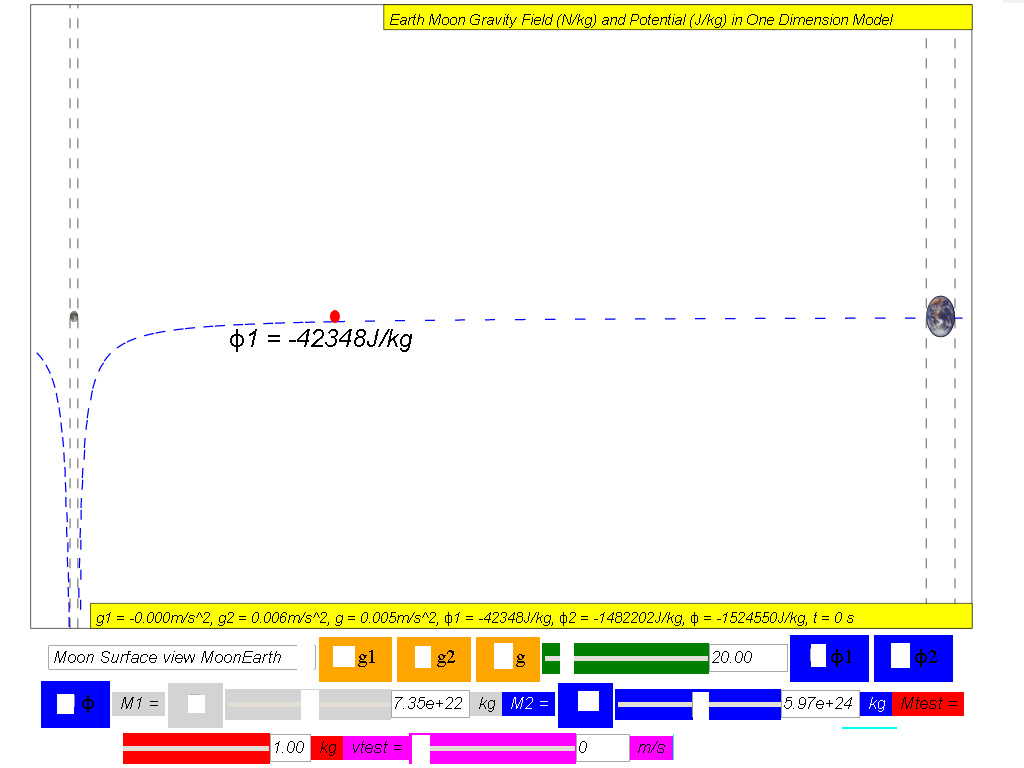
φ1 =
Gravitational potential due to Moon
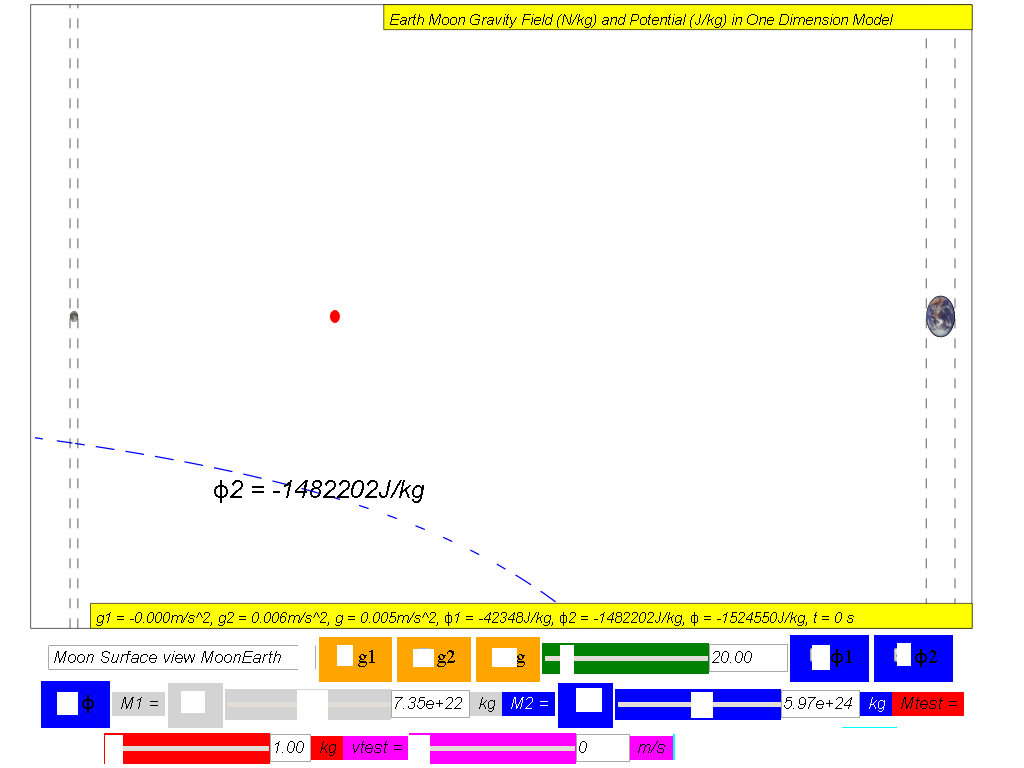φ2 =
Gravitational potential due to Earth
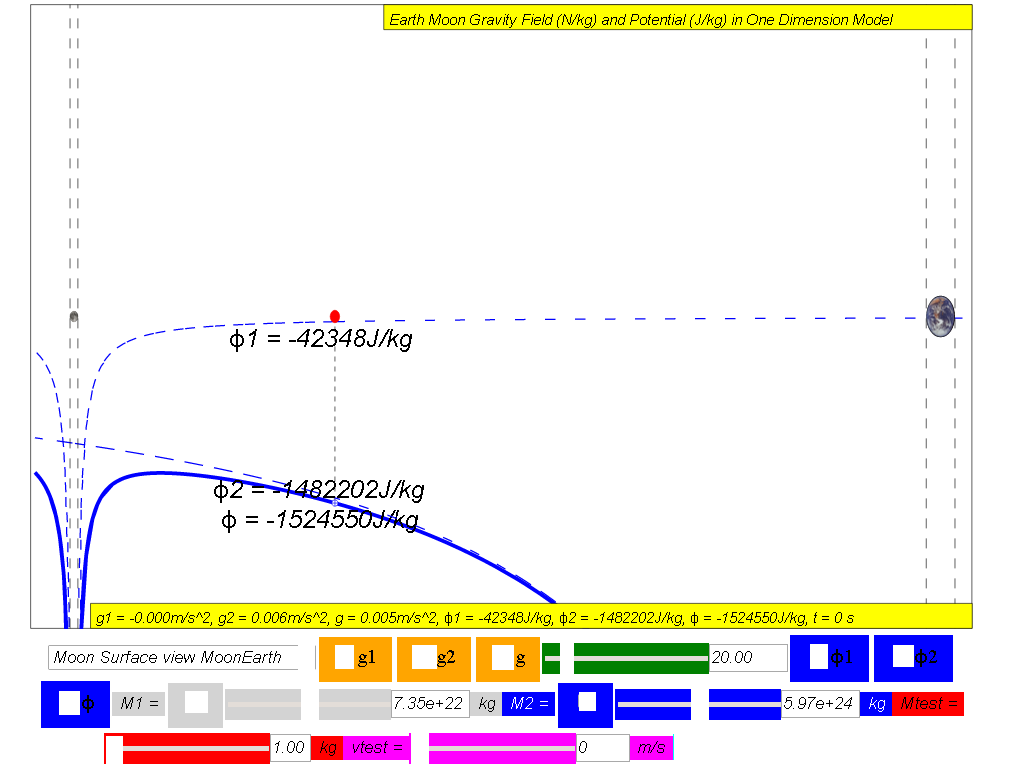
φtotal =
φ1 +φ2 = Net
gravitational potential along the line of centres is equal to the
sum of the gravitational potentials due to the Earth and Moon
work in progress: in an
illustration scenario, the Masses M1 and M2 can be vary as well as
their positions to provide a clearer example as shown below.
Escape
Speed
Is it true that “what goes up must come
down”?
It is only accurate to say that “what
goes up may come down”. There is a critical speed at which
an object can be launched such that it can escape the Earth
permanently. Such a critical speed is termed as the escape
speed.
Example
Determine an expression for the escape
speed, v, of a rocket of mass m launched from the surface of Earth
of mass M and radius R.
By conservation of energy, assuming at r
= ∞, the
minimum speed is 0.
KEearth
surface +
PEearth surface =
KE∞ + PE∞
v = 1.12x104 m/s
Therefore, to escape from Earth, it
implies that the projectile must have a minimum velocity of v =
1.12x104 m/s .
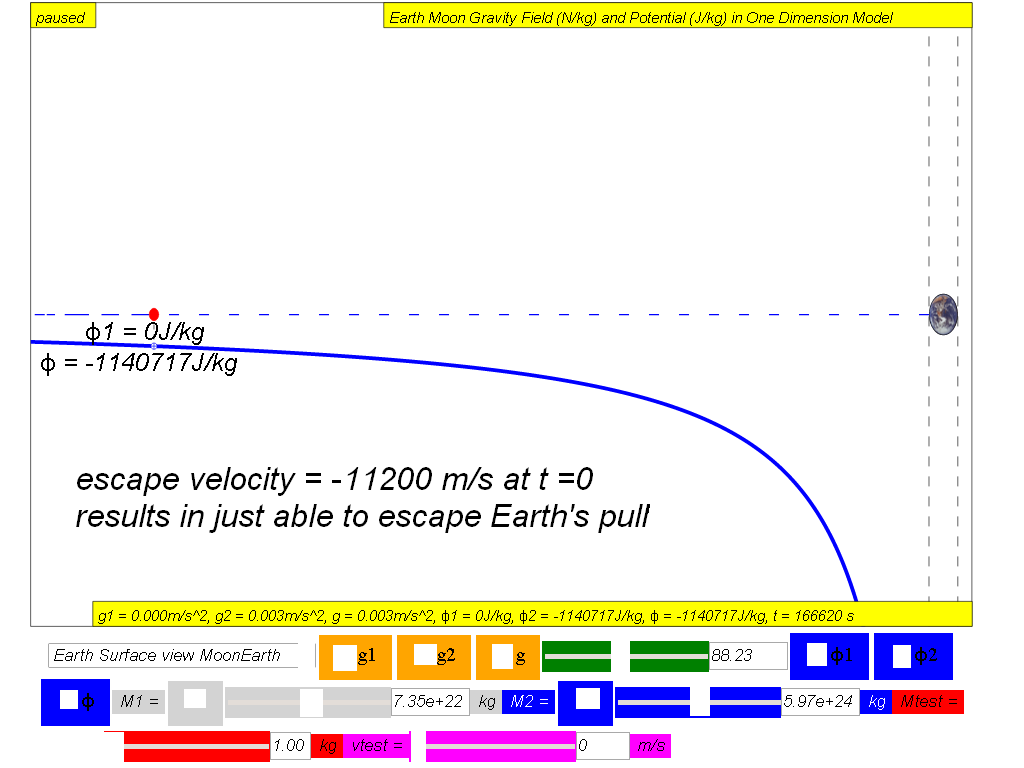
To understand the escape velocity
concept, the following steps could be used as an inquiry approach
to experience escape velocity in the context of the simulation.
- uncheck the M1 moon to remove the effects of the Moon
- select from the drop-box menu the option Earth Surface view
MoonEarth (Left to Right), and notice the test mass (red) is
placed on the surface of the Earth on the right side.
- key in on the vtest, velocity of the test mass (magenta) say
-10000 m/s (negative as the velocity shoot to the left of the
Cartesian coordinate system)), and click play to observe the
effects of launching a projectile at this speed. You could
record your observation as "unable to escape from Earth's
gravity pull.
similarly, design an experiment to
discover the minimum theoretical speed to escape from Earth's
pull.
can you conclude that any velocity
lesser than v = 1.12x104 m/s
cannot allow the projectile to escape from Earth's pull?
can you conclude that any velocity
greater than vescape Earth =
1.12x104 m/s allow
the projectile to escape from Earth's pull?
Similarly, you can derive the
theoretical escape velocity from Earth's Moon surface and test it
on the simulation?
answer: vescape
Moon=2400 m/s
given that root-mean-square speed is the
measure of the speed of particles in a gas that is most convenient
for problem solving within the kinetic theory of gases, is given by
Given gas constant R = 8.31 J K−1 mol−1, molar mass of water is Mm H20 = 18x10-3 kg/mol
, T is temperature in Kelvin, using the minimum therotical speed
from Moon, suggest the temperature of Moon surface at some point
in its history where Moon surface does not have water.
T = 4.2x103 K
With this limited information, this data
seems to suggest at some point of Moon's history, it could be very
hot like T = 4.2x103 K
and as the Moon cools, not enough water molecules was able to form
on the Moon's surface to form oceans like what we have on Earth.
Java
Model
http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejs/ejs_model_GFieldandPotential1Dv7EarthMoon.jar
Model
https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_gravity11/gravity11_Simulation.xhtml