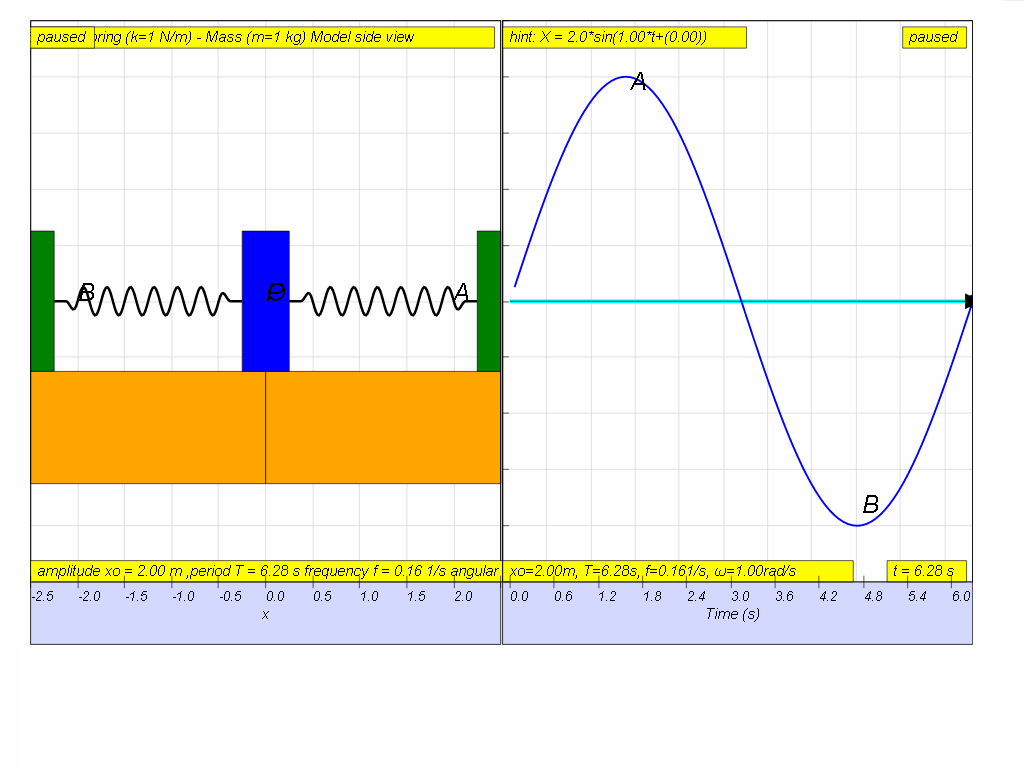
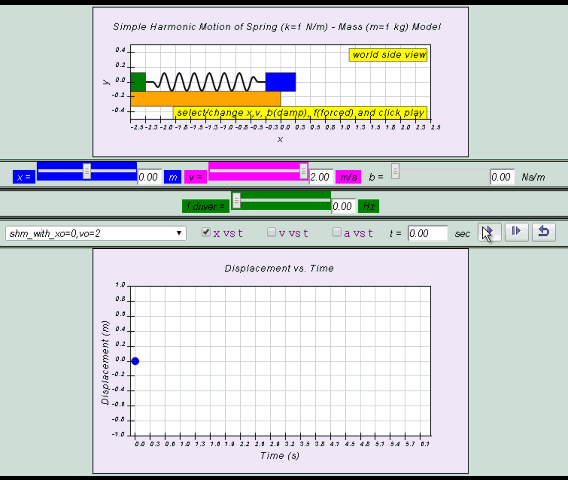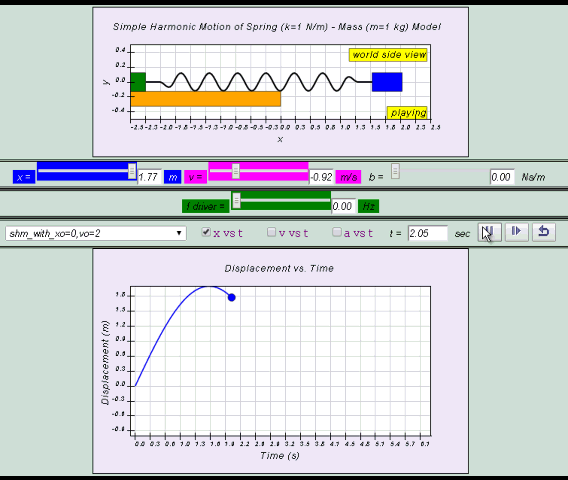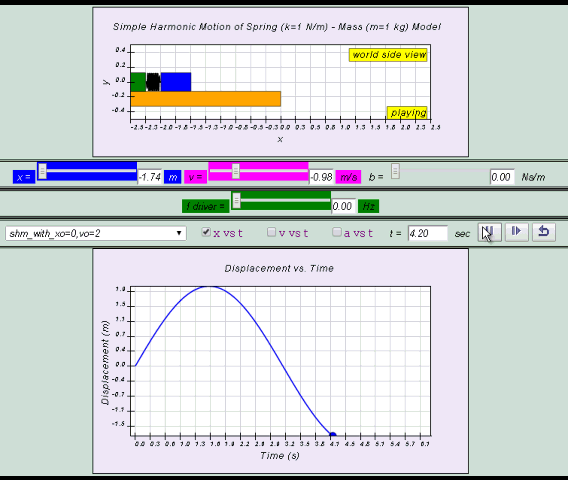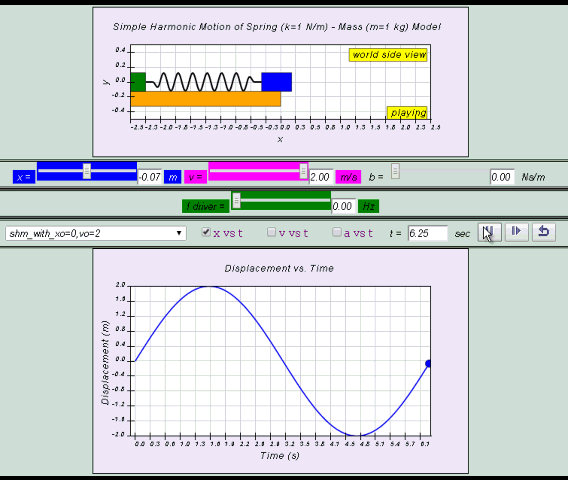
The displacement of a spring mass system from a fixed point is as shown. From the graph, determine the
(a) amplitude,
(b) period,
(c) frequency,
(d) angular frequency, of the oscillations.
[2.00 m, 6.28 s, 0.159 Hz, 1.00 rad s–1]
Q1: Consider an object P oscillating between point A and B about
the origin (0,0), assuming the usual Cartesian Coordinate System
apply. Observe the Model and suggests possible meaning of
the following points with the most suitable descriptions.
central equilibrium position
instantaneous position
maximum amplitude m
minimum amplitude m
Given the equation x = x0 sin ( ω t ) can describe SHM, suggests the usual symbols associated to the physical quantity
central equilibrium position
instantaneous position or displacement given by vector OP m
maximum amplitude m
minimum amplitude m
time taken for one complete oscillation, for example Path from O→A→O→B→O s
number of oscillations performed per unit time 1/s. Hence, f and T are related by the equation
angular
frequency
rad/s. Since one
complete oscillation is 2π radians, ω and f are related by ω = 2π
f

The displacement of a spring mass system from a fixed point is as
shown. From the graph, determine the
(a) amplitude,
(b) period,
(c)
frequency,
(d) angular frequency, of the oscillations.
[2.00 m, 6.28 s, 0.159 Hz, 1.00 rad s–1]
https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_SHM04/SHM04_Simulation.xhtml
Q1: run model with different starting y to explore the meaning of
amplitude
Q2: run model with different mass m and spring constant k to
explore different period T, frequency f and angular frequency ω