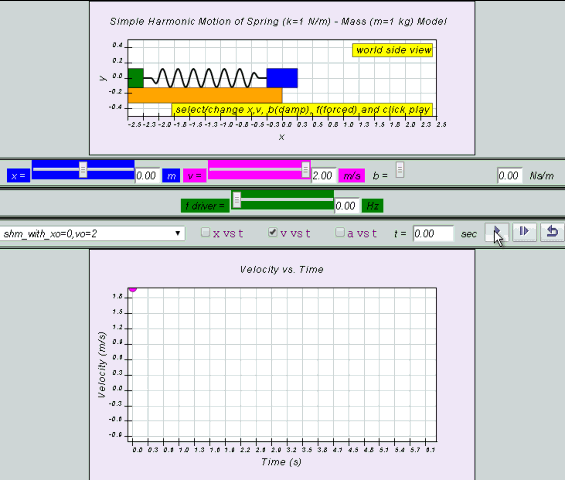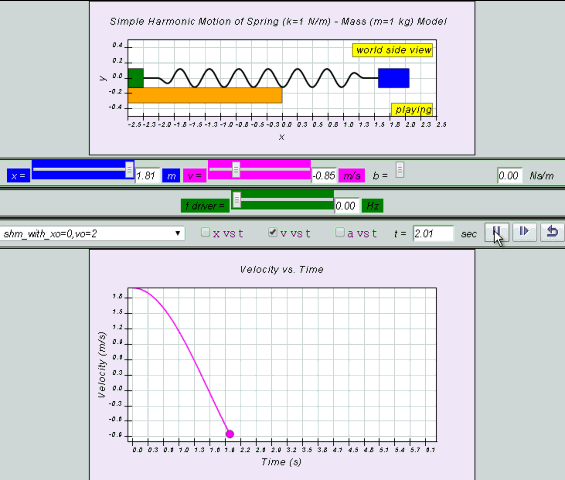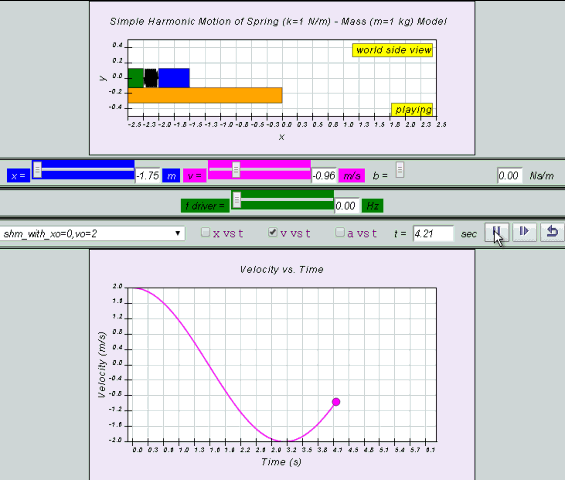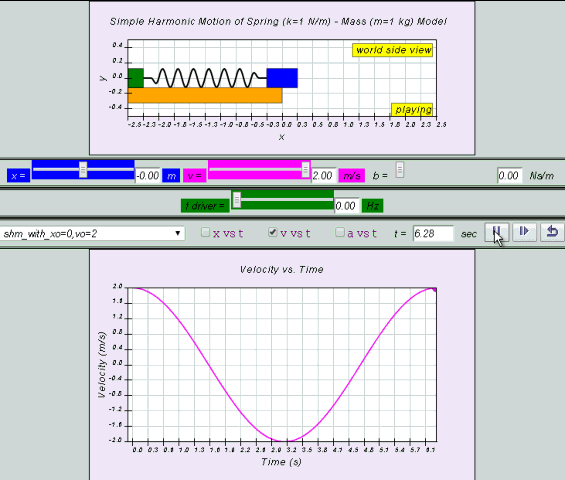
x= x0 sin( ωt )
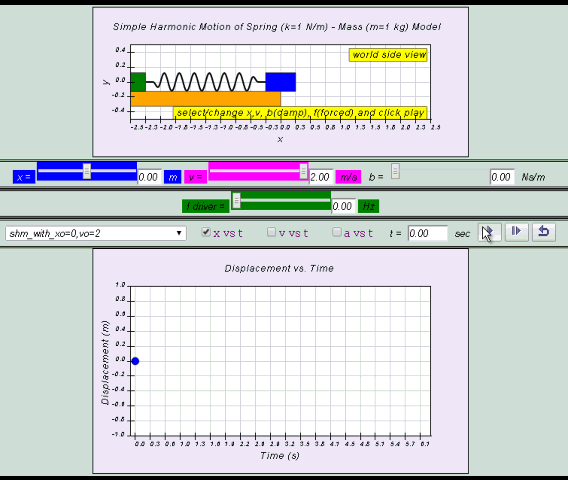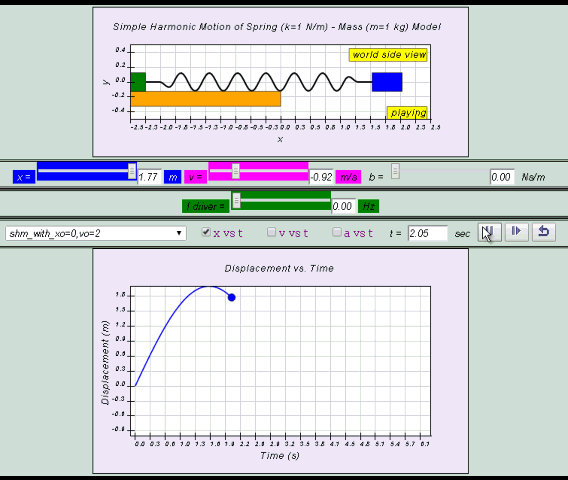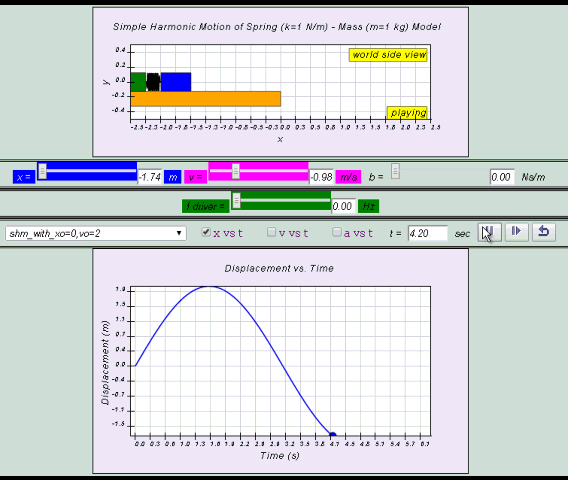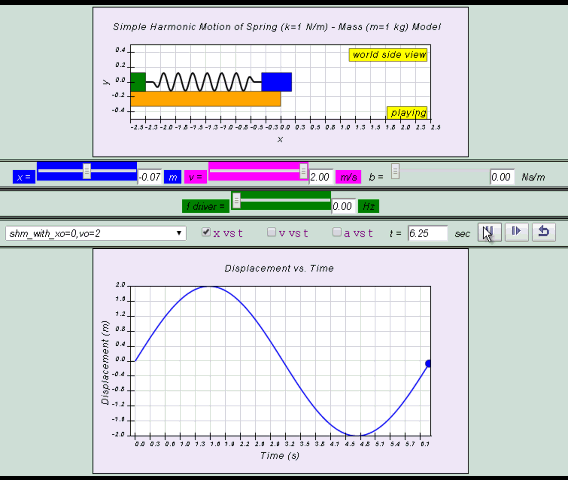
x= x0 sin( ωt )

equation for v can also be obtained by differentiating x with respect to time t.
v = x0 ω cos (ωt ) =
v0 cos
(ωt)
equation for a can also be obtained by differentiating v with respect to time t.
a = - x0 ω2 sin (ωt ) = - a0 sin (ωt)
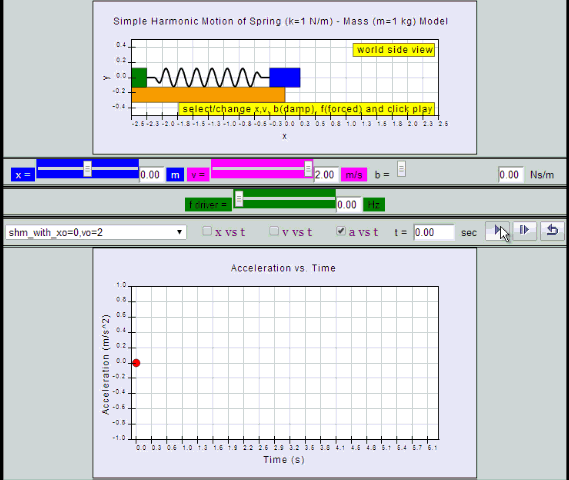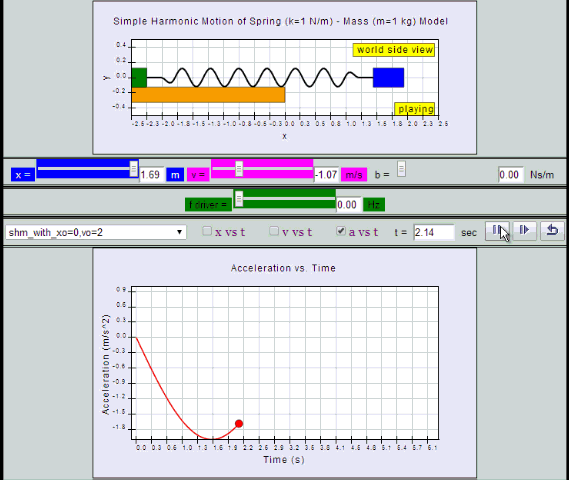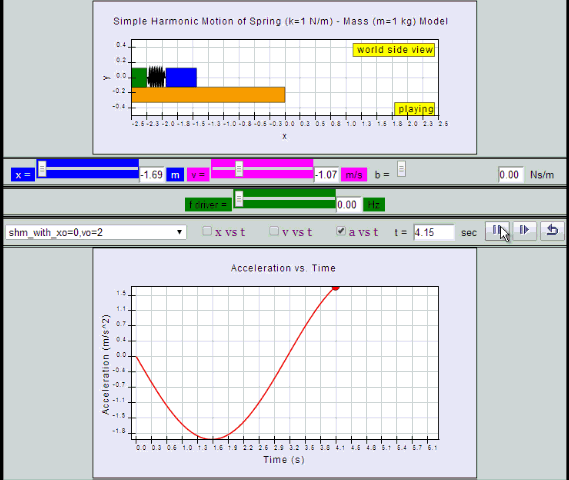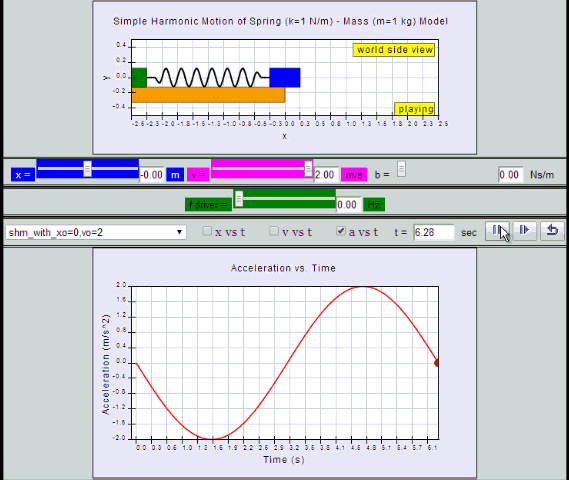
by substitution, suggest if the defining equation a = - ω2 x is true or false.
| Quantity | extreme left | centre equilibrium | extreme right |
| x | – x0 | 0 | x0 |
| v | 0 | + x0ω when v >0
or – x0ω when v <0 which are maximum values |
0 |
| a | +x0ω2 | 0 | –x0ω2 |