Example 2: Spring-mass system

1.2.11 Example: Spring-mass system

A mass suspended from a spring, displaced vertically and released to move freely to produce up and down motion

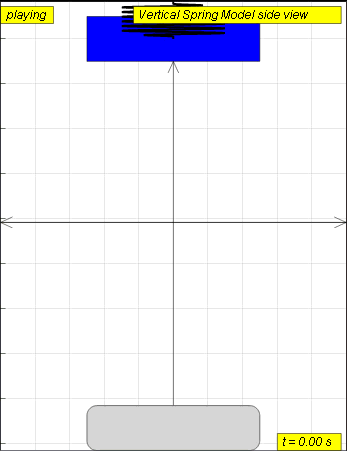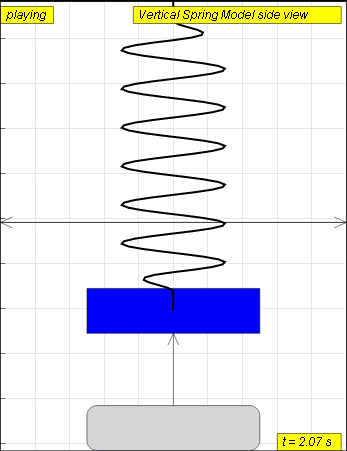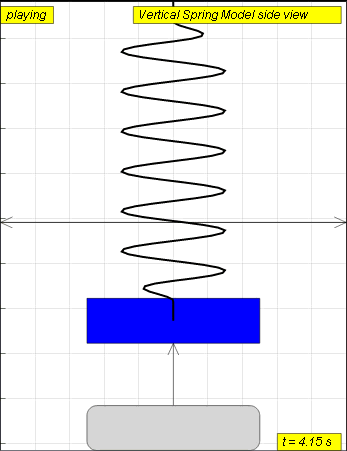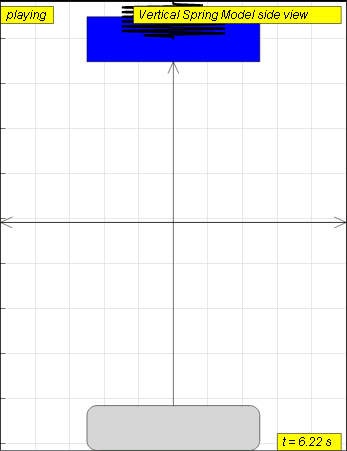
The model view of a mass suspended from a spring, displaced vertically and released to move freely to produce up and down motion with right panel showing the displacement, velocity and acceleration.

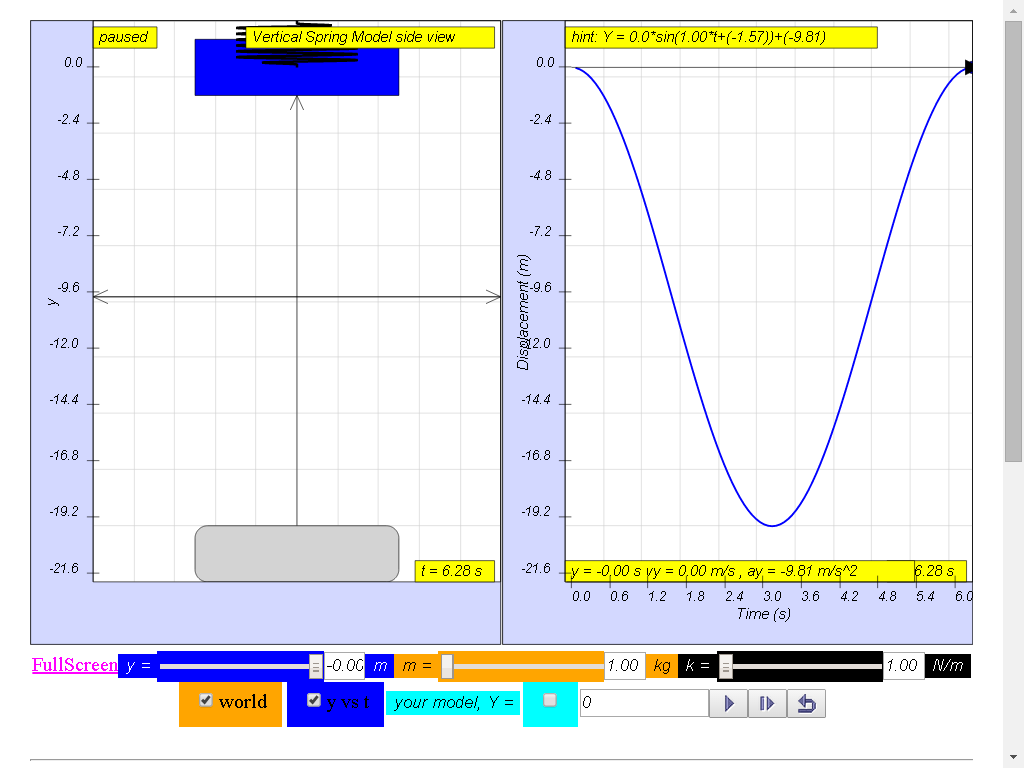
Q1: under what conditions would this vertical spring mass system’s motion be not well modeled as a simple harmonic motion?

H1: the model assumes the restoring force by the spring is F = -ky, it is always correct for any magnitude of oscillation y in real springs. Is it always valid in the real spring motion when the spring is hyper extending beyond the linear limits of Hooke's Law ?

Q2: change the simulation y=0 m and Play the model. In the your model Y = _________, suggest your own suitable model that can describe the motion y.

Q3: in this same motion, propose the velocity and acceleration model(s)

Q4: carry out some other conditions, verify that the general equations for displacments if can be model by Y = Y₀sin(ωt+φ)+Y_shift where the usual symbols have the usual meaning. Hence or otherwise, Suggest with reasons, the meaning of Y₀ , ω , φ , and Y_shift.

Q5: similarly, suggest whether the model(s) for velocity, v_Y =ωY₀cos(ωt+φ) and

a_Y = - ω²Y₀sin(ωt+φ). Test them out using an example of your choice.

1.2.11.1 YouTube

http://youtu.be/P-Umre5Np_0 MIT Physics Demo -- Spray Paint Oscillator. A can of spray paint is attached to a spring oscillator. A roll of paper is run past the oscillating can. The result is a sine wave - http://en.wikipedia.org/wiki/Sine_wave - on the paper.Watch the original video on MIT TechTV - http://techtv.mit.edu/videos/803-spray-paint-oscillator

1.2.11.2 Tracker activity:

http://weelookang.blogspot.sg/2012/08/tracker-modeling-in-spring-mass-system.html

1.2.11 Example: Spring-mass system

Q1: under what conditions would this vertical spring mass system’s motion be not well modeled as a simple harmonic motion?

Q2: change the simulation y=0 m and Play the model. In the your model Y = _________, suggest your own suitable model that can describe the motion y.

Q3: in this same motion, propose the velocity and acceleration model(s)

Q4: carry out some other conditions, verify that the general equations for displacments if can be model by Y = Y0sin(ωt+φ)+Yshift where the usual symbols have the usual meaning. Hence or otherwise, Suggest with reasons, the meaning of Y0 , ω , φ , and Yshift.

Q5: similarly, suggest whether the model(s) for velocity, vY =ωY0cos(ωt+φ) and

aY = - ω2Y0sin(ωt+φ). Test them out using an example of your choice.

1.2.11.1 YouTube

1.2.11.2 Tracker activity:

1.2.11.3 Model:

Q4: carry out some other conditions, verify that the general equations for displacments if can be model by Y = Y₀sin(ωt+φ)+Y_shift where the usual symbols have the usual meaning. Hence or otherwise, Suggest with reasons, the meaning of Y₀ , ω , φ , and Y_shift.

Q5: similarly, suggest whether the model(s) for velocity, v_Y =ωY₀cos(ωt+φ) and

a_Y = - ω²Y₀sin(ωt+φ). Test them out using an example of your choice.