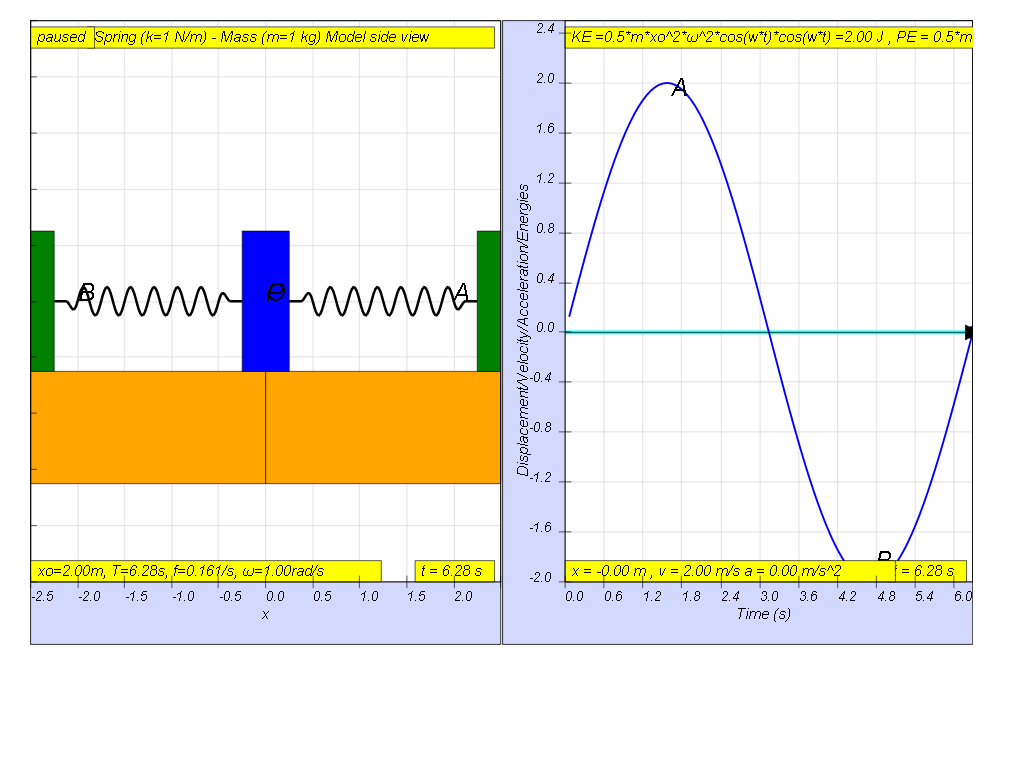
If the variation with time of displacement is as shown, then the energies should be drawn as shown.
recalling Energy formula

If the variation with time of displacement is as shown, then the
energies should be drawn as shown.
recalling Energy formula
PE = ½ k x2
in terms of time t,
x = x0 sin(ωt)
differentiating with t gives
v = v0 cos (ωt)
therefore, KE = ½ m v2= ½ m (v0 cos (ωt))2= ½ m (x02ω2)cos (ωt))2
PE = ½ k x2= ½ (mω2 )(x0 sin (ωt))2=
½ m (x02ω2 )sin (ωt))2
therefore total energy is a constant value in the absence of
energy loss due to drag (resistance)
TE = KE + PE = ½ m (x02ω2 )[cos2(ωt)
+ sin2(ωt))] = ½ m (x02ω2)
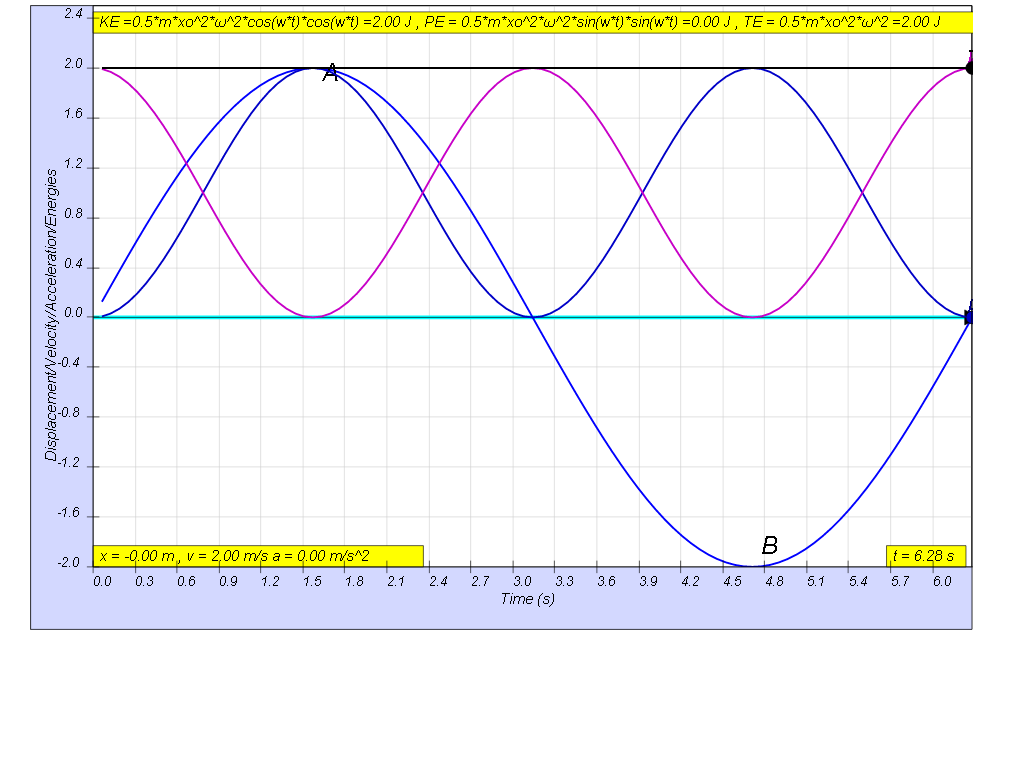
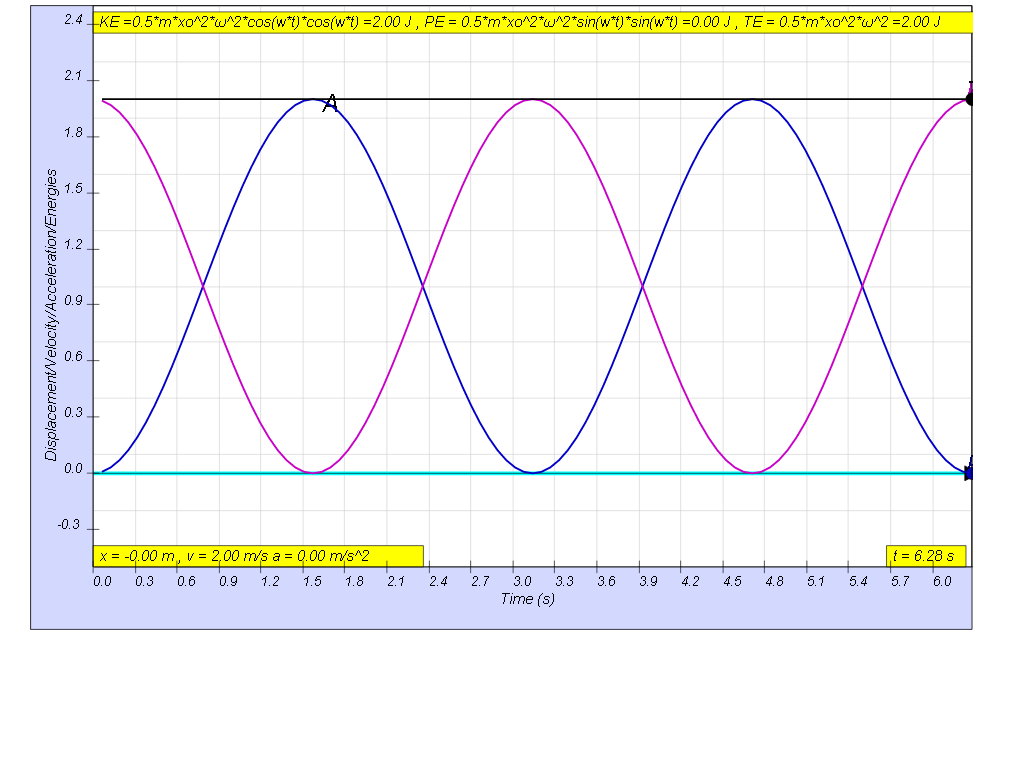
| general energy formula | SHM energy formula | when t = 0 | when t = T/4 | when t = T/2 | when t = 3T/4 | when t = T |
| KE = ½ m v2 | ½ m (x02ω2)cos (ωt))2 | ½ m (x02ω2) | 0 | ½ m (x02ω2) | 0 |
½ m (x02ω2) |
| PE = ½ k x2 | ½ m (x02ω2)cos (ωt))2 | 0 | ½ m (x02ω2) | 0 | ½ m (x02ω2) | 0 |
| TE = KE + PE | TE = ½ m (x02ω2) | ½ m (x02ω2) | ½ m (x02ω2) |
½ m (x02ω2) |
½ m (x02ω2) | ½ m (x02ω2) |