Degrees
of damping
LO (i)
If no frictional forces act on an oscillator (e.g.
mass-spring system, simple pendulum system, etc.), then it
will oscillate indefinitely.
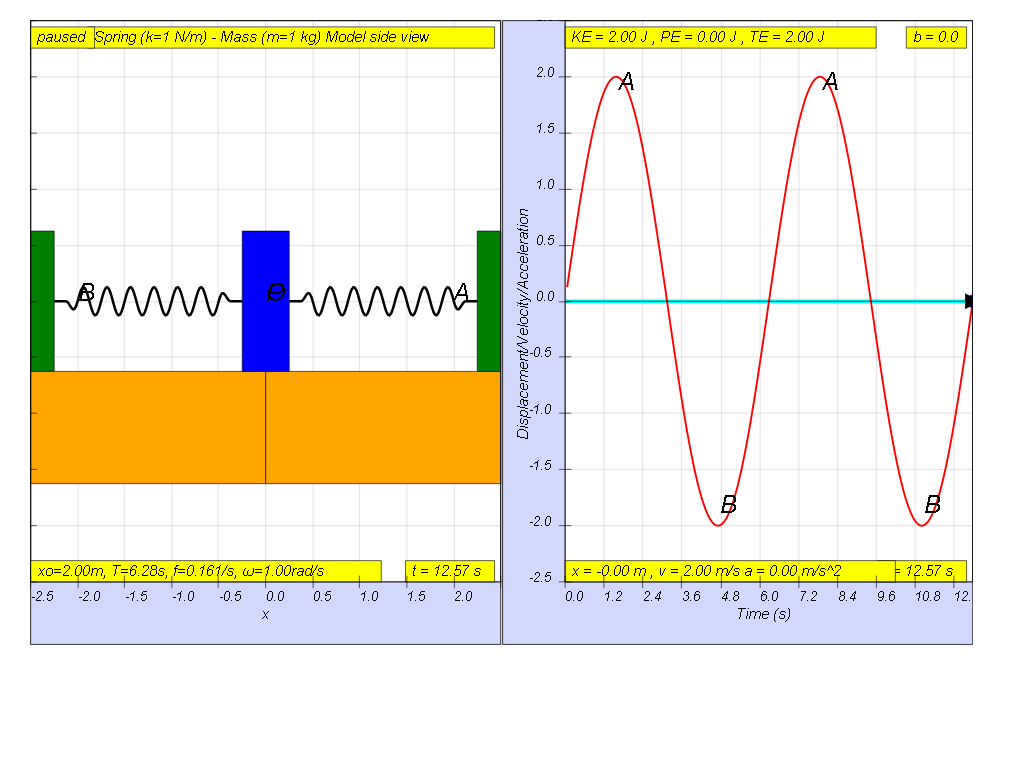
In practice, the amplitude of the oscillations decreases to zero
as a result of friction. This type of motion is called damped
harmonic motion. Often the friction arises from air resistance
(external damping) or internal forces (internal damping).
if
the motion is x= x0 sin(ωt),
the following are the x vs t graphs for 2 periods, as an
illustration of the damping.
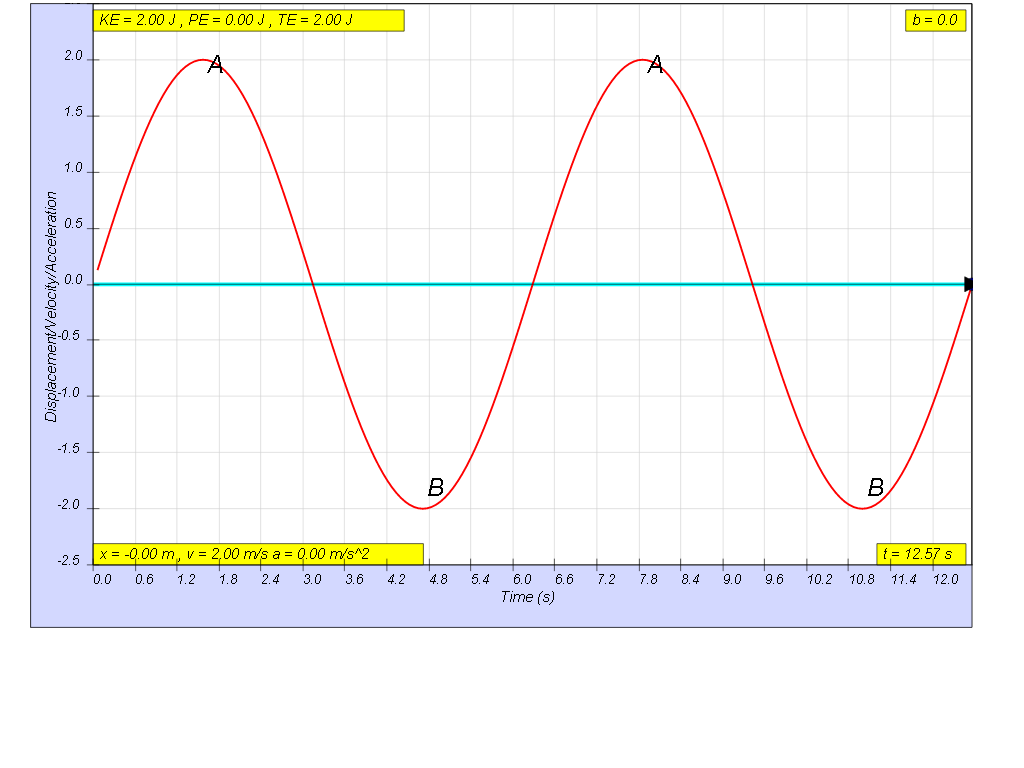
when b=0.0 no damping, system oscillates forever without coming
to rest. Amplitude and thus total energy is constant
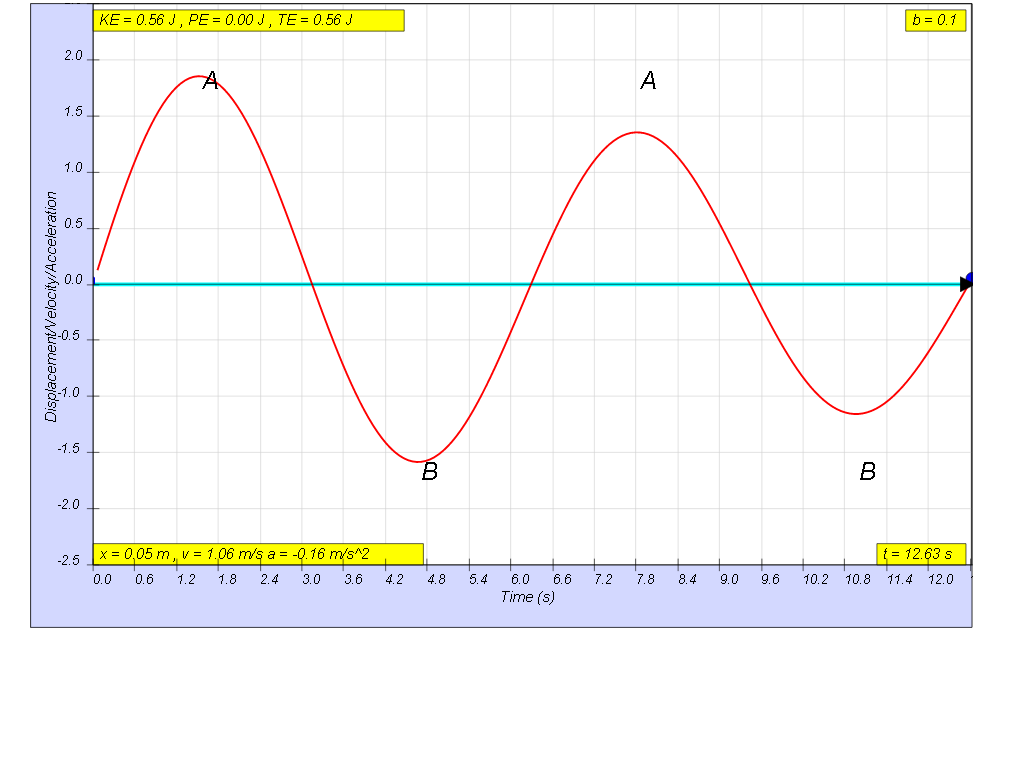
when b=0.1 very lightly damp, system
undergoes several oscillations of decreasing amplitude before
coming to rest. Amplitude of oscillation decays exponentially with
time.
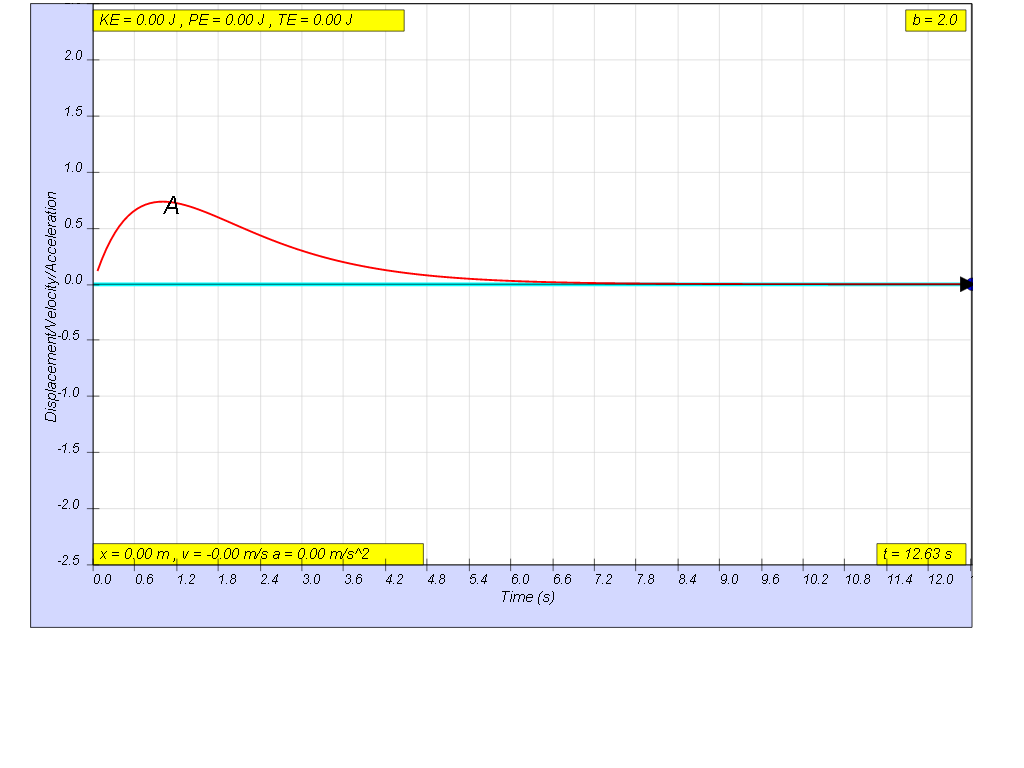
when b=2.0, critically damp system returns to equilibrium in the
minimum time, without overshooting or oscillating about the
equilibrium position amplitude.
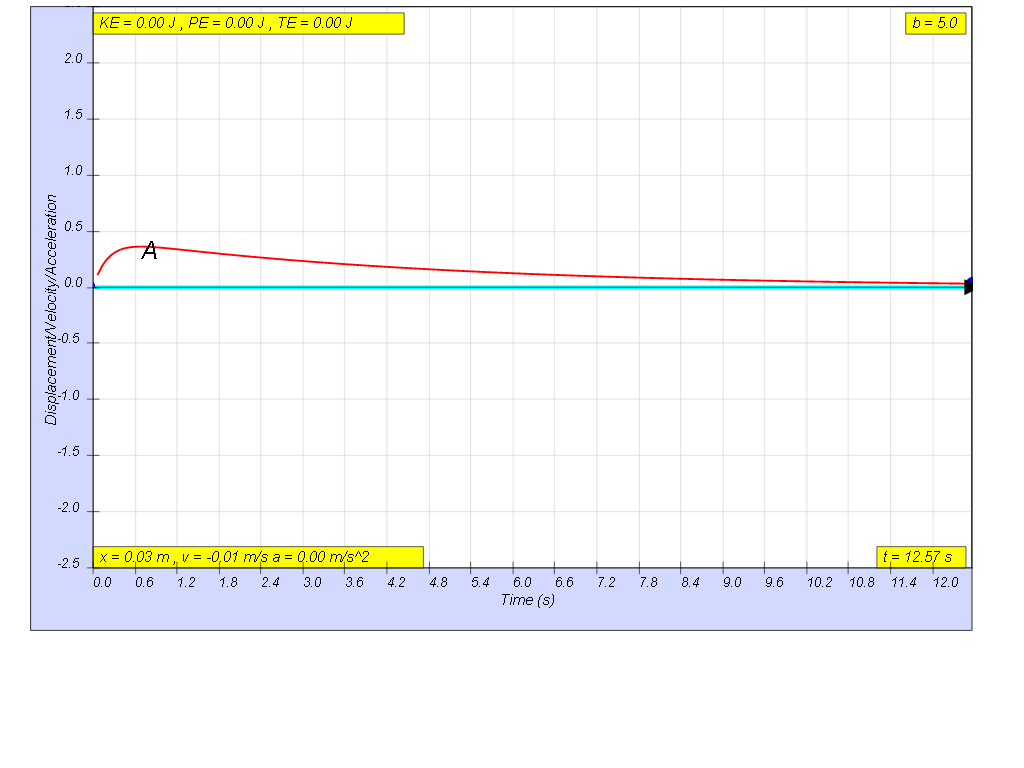
when b=5.0, very heavy damp, system returns to equilibrium very slowly
without any oscillation
a
more typical starting position, is x= x0 cos(ωt), the
following are the x vs t graphs for 2 periods, as an illustration
of the damping.
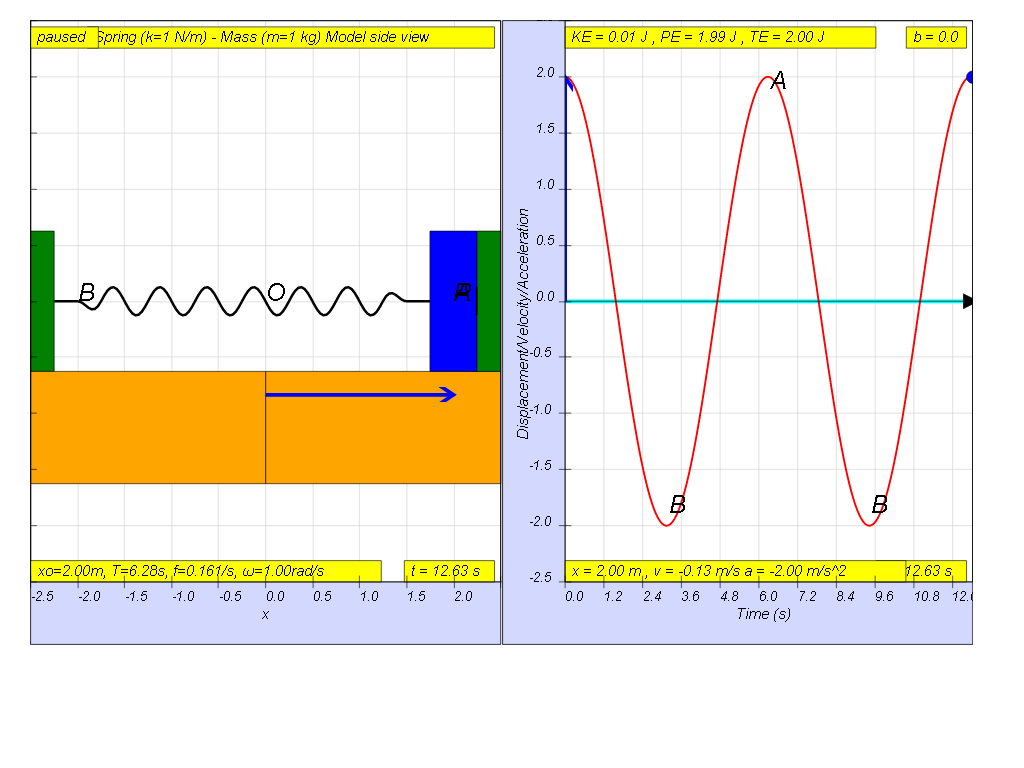
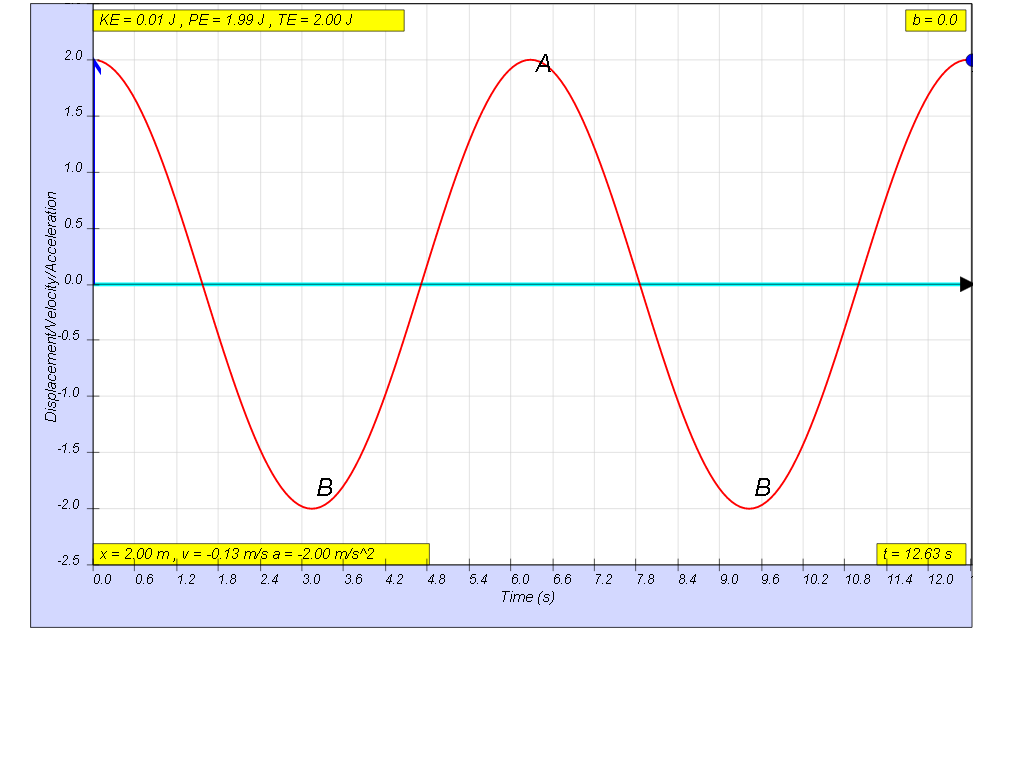
when b=0.0 no damping, system oscillates forever without coming
to rest. Amplitude and thus total energy is constant
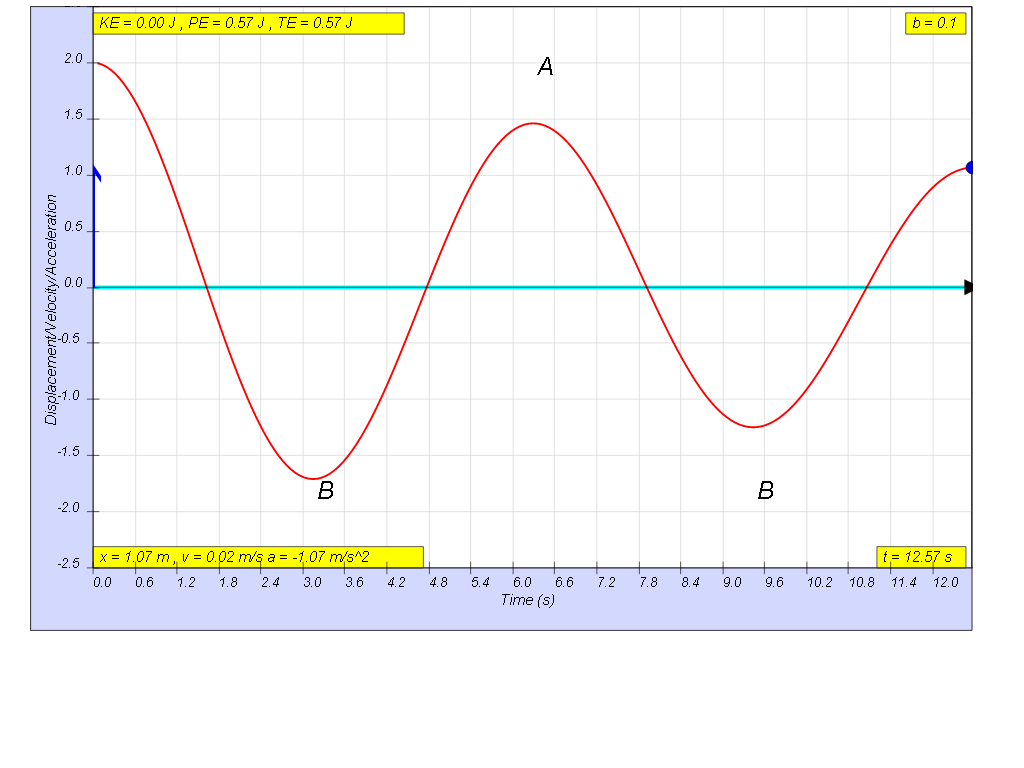
when b=0.1 very light damping, system
undergoes several oscillations of decreasing amplitude before
coming to rest. Amplitude of oscillation decays exponentially with
time.
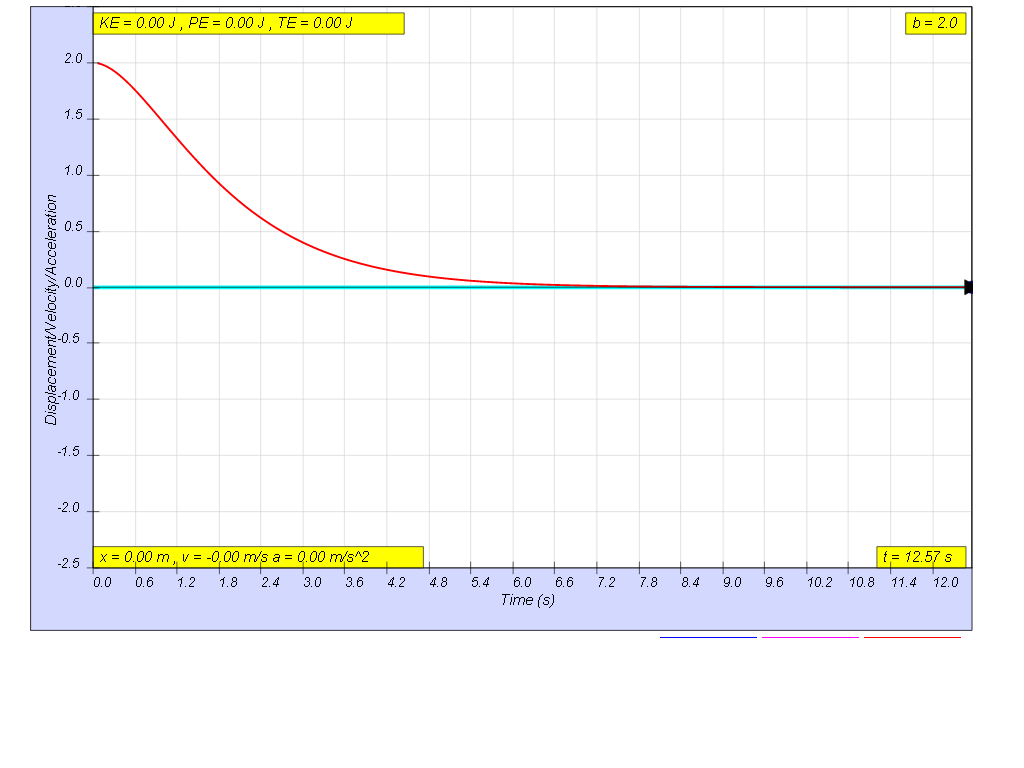
when b=2.0 critically damp, system returns to equilibrium in the
minimum time, without overshooting or oscillating about the
equilibrium position amplitude.
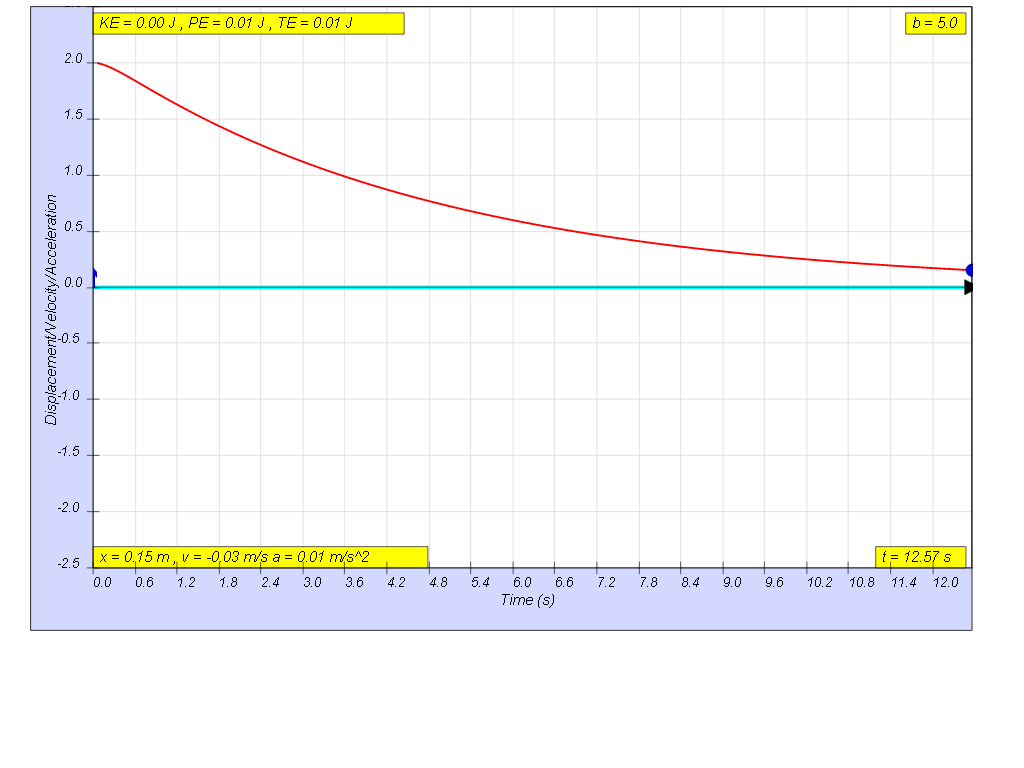
when b=5.0 very heavy damp, system returns to equilibrium very slowly
without any oscillation.
Model:
http://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_SHM20/SHM20_Simulation.xhtml









