the following were reference for the customized of this model.
- wolfgang and lookang http://weelookang.blogspot.com/2010/06/open-source-ejs-superposition-of-2.html
- One Dimensional Wave Superposition JS Model by Wolfgang Christian and Francisco Esquembre http://www.compadre.org/osp/items/detail.cfm?ID=13014
Description:
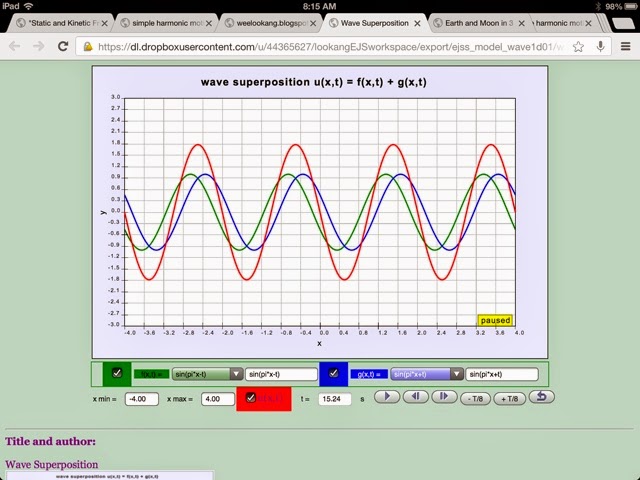
The EJSS wave 1d superposition model shows
how the superposition principle gives rise to
wave phenomena such as standing waves and beats. Users
enter real-valued wave functions and
dropdown menu for ease of inputs and
observe both the time dependent functions and their
superposition. This model uses the JavaScript mathematical
function parser.
A wave is a disturbance, such as sound, that propagates through space. For a wave propagating in one dimension, we use a wave function u(x,t) to represent the wave at position x and time t as shown in the screen shot. Although a sinusoidal wave function is a very common type type of disturbance, we should remember that there are many other wave functions, such as shock waves, that do not fit this functional form.
The EJSS wave 1d superposition model was developed using the Easy Java Simulations (EJS) version 5. It is distributed as a ready-to-run html page and requires only a browser with JavaScript support.
A wave is a disturbance, such as sound, that propagates through space. For a wave propagating in one dimension, we use a wave function u(x,t) to represent the wave at position x and time t as shown in the screen shot. Although a sinusoidal wave function is a very common type type of disturbance, we should remember that there are many other wave functions, such as shock waves, that do not fit this functional form.
The EJSS wave 1d superposition model was developed using the Easy Java Simulations (EJS) version 5. It is distributed as a ready-to-run html page and requires only a browser with JavaScript support.
The mathematical equation used are:
which the resultant is
the dropdown menu has some function typical in the A level
Physics
["sin(pi*x-t)","0.5*sin(pi*x-t)","2*sin(pi*x-t)","sin(0.5*pi*x-t)","sin(2*pi*x-t)","sin(pi*x-0.5*t)","sin(pi*x-2*t)","sin(pi*x-t-0.785)","sin(pi*x-t-1.57)"]
["sin(pi*x+t)","0.5*sin(pi*x+t)","2*sin(pi*x+t)","sin(0.5*pi*x+t)","sin(2*pi*x+t)","sin(pi*x+0.5*t)","sin(pi*x+2*t)","sin(pi*x-t+0.785)","sin(pi*x-t+1.57)"]
in general:
Changes:
- recreate on a fresh ejss using codes from http://www.compadre.org/osp/items/detail.cfm?ID=13014
- use design ideas from http://weelookang.blogspot.com/2010/06/open-source-ejs-superposition-of-2.html
- fix a bug in the input fields need _view._update(); //critical for immediate update
Area of improvement: Done!
- cannot figure out how to make a dot that travels on
the
f(x,t) andg(x,t)
the generic wave form has an equation of this form:
f(x,t)=sin(πx−k1t)
wave moves to the right
g(x,t)=sin(πx+k2t)
wave moves to the left