EXERCISE 1: OBTAIN AND USE INFORMATION FROM PEER-REVIEWED LITERATURE

Water and air are the two materials involved with producing rainbows we may see in the sky after a thunderstorm. To accurately predict where rainbows will appear, we need to have accurate information about the refractive indices of water and air.

(a) Obtain a copy of “Models for the wavelength dependence of the index of refraction of water”, Applied Optics 36 (16), 3785-3787 (1997) by Paul D.T. Huibers, and use Eq. (3) of that paper to generate a plot of the refractive index of water as a function of wavelength in the range from 400 to 650 nm.

(b) Obtain a copy of “Refractive index of air: new equations for the visible and near infrared”, Applied Optics 35(9), 1566-1573 (1996) by Philip E. Ciddor, and use Eq. (1) of that paper to generate a plot of nair−1$n_{air}-1$, the deviation of the refractive index of air from unity, as a function of wavelength in the range from 400 to 650 nm.

Which material has the larger change in refractive index over the wavelength range from 400 to 650 nm? Calculate the ratio of the larger change to the refractive index of the material for a wavelength of 400 nm, and comment on the magnitude of the ratio.

EXERCISE 2: DEFLECTION ANGLE FOR A LIGHT RAY ENTERING A SPHERICAL RAINDROP

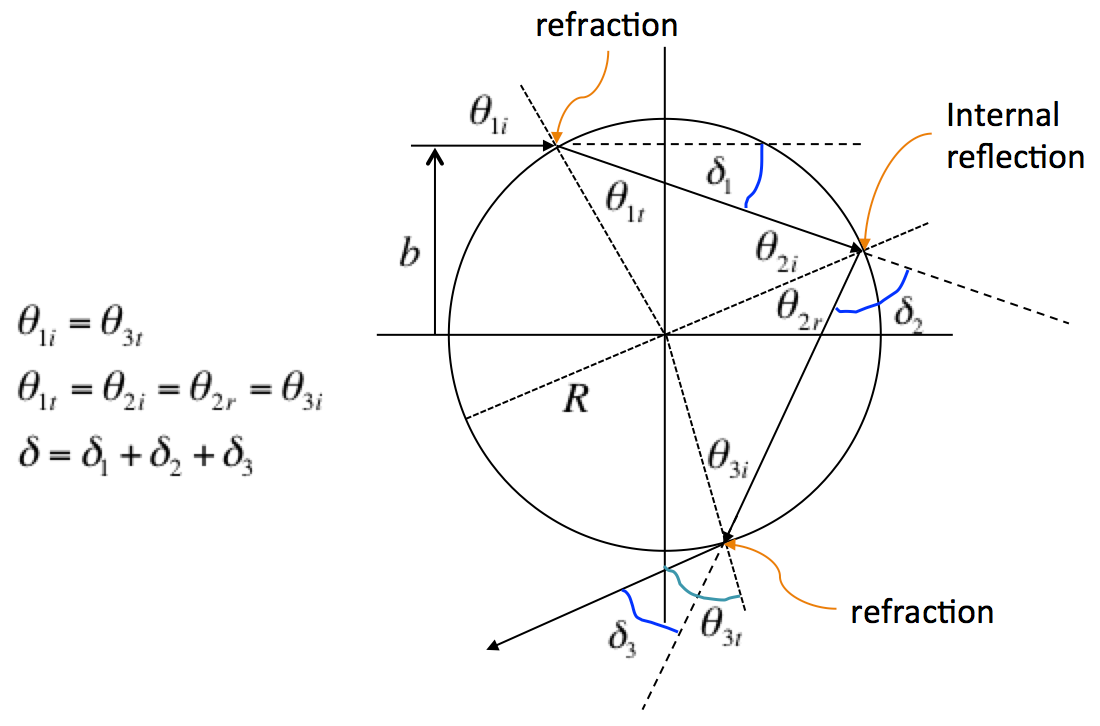
Assume that a light ray incident on a spherical raindrop at an angle θ1i${\theta }_{1i}$ measured with respect to the surface normal undergoes one internal reflection before leaving the raindrop, as shown below.

`

Show that if θi≡θ1i${\theta }_i\equiv {\theta }_{1i}$ and θr≡θ1t${\theta }_r\equiv {\theta }_{1t}$, then the deflection angle δ$\delta$ of the light ray is (in radians):

The deflection angle δ$\delta$ is the angle between the incident ray and the outgoing ray, and θr${\theta }_r$ is the angle of refraction for the light ray incident from air and entering water. To compute the deflection angle, what quantities must be known?

EXERCISE 3: COMPUTE THE DEFLECTION ANGLE VERSUS INCIDENT ANGLE

Generate a plot of the deflection angle δ$\delta$ as a function of incident angle θi${\theta }_i$ for light rays of wavelength 400 nm that experience one internal reflection in the raindrop. Compare, on the same plot, the deflection angle for light rays of wavelength 650 nm. The two curves should have minima that are close to each other, but not identical. What are the values of the incident angle corresponding to these two minima? Assuming that these minima correspond to the rainbow direction, what direction do you have to look relative to the horizontal to see the bright red band of the rainbow? What direction do you have to look relative to the horizontal to see the bright violet band? Which band appears higher in the sky?

Near the minimum of the deflection function (that is, the δ(θi)$\delta ({\theta }_i)$ curve), are two rays with slightly different incident angles deflected into different directions? Regarding the brightness of the deflected light perceived by an observer, what is implied by your answer?

EXERCISE 4: WHERE IS THE SECONDARY (DOUBLE) RAINBOW?

Repeat the computation of Exercise 3, but now assume that the ray undergoes two internal reflections within the raindrop. In this case, show that the deflection angle is given by

and plot the deflection angle versus the incident angle for rays of wavelength 400 nm and 650 nm. The two curves should have minima that are close to each other, but not identical. What are the values of the incident angle corresponding to these two minima? Assuming that these minima correspond to the rainbow direction, what direction do you have to look relative to the horizontal to see the bright red band of the secondary rainbow? Can a ground based observer see these rays? Do the rays that produce the secondary rainbow enter the top of the raindrop? What direction do you have to look relative to the horizontal to see the bright violet band? Which band appears higher in the sky?

Near the minimum of the deflection function (that is, the δ(θi)$\delta ({\theta }_i)$ curve), are two rays with slightly different incident angles deflected into different directions? Regarding the brightness of the deflected light perceived by an observed, what is implied by your answer?

EXERCISE 5: CRUDE ESTIMATE OF THE IRRADIANCE VERSUS DEFLECTION ANGLE FOR A SINGLE WAVELENGTH: PRIMARY RAINBOW

Assume that the each outgoing ray produces an irradiance that is equal to I(θ)=I0exp[−(θ−δ)2]$I(\theta )=I_0\exp [-(\theta -\delta {)}^2]$ where here the angles are assumed to be in degrees and the implied width of this distribution is 1∘$1^{\circ }$. (For simplicity, we neglect the loss of intensity during refraction and internal reflection. This is a huge oversimplification, but it allows us to focus on adding up contributions from each ray.) Sum up the contributions from rays uniformly distributed over the scaled impact parameter b~=b/R$\tilde{b}=b/R$ to compute the overall irradiance as a function of deflection angle for light of wavelength 400 nm. Plot the resulting irradiance distribution versus deflection angle for a single wavelength. How does this plot help explain why the rainbow is bright?