Ejs Open Source 1 Dimension Doppler Effect Sound Wave Java Applet

Ejs Open Source 1 Dimension Doppler Effect Sound Wave Java Applet

update: 26 November 2013: bug fixed

Ejs Open Source 1 Dimension Doppler Effect Sound Wave Java Applet with features like 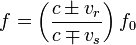$f = \left( \frac{c \pm v_r}{c \mp v_{s}} \right) f_0 \,$ , counters for waves emitted and detected
http://weelookang.blogspot.sg/2011/09/ejs-open-source-1-dimension-doppler.html
author: lookang based on the works on Fu-Kwun Hwang, Juan M. Aguirregabiria and Andrew Duffy
https://dl.dropboxusercontent.com/u/44365627/lookangEJSS/export/ejs_model_dopplerxywee01.jar
https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejs_model_dopplerxywee01.jar
https://dl.dropbox.com/u/44365627/lookangEJSworkspace/export/ejs_users_sgeducation_lookang_dopplerxywee.jar

Ejs Open Source 1 Dimension Doppler Effect Sound Wave Java Applet with features like 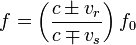$f = \left( \frac{c \pm v_r}{c \mp v_{s}} \right) f_0 \,$ , counters for waves emitted and detected
http://weelookang.blogspot.sg/2011/09/ejs-open-source-1-dimension-doppler.html
author: lookang based on the works on Fu-Kwun Hwang, Juan M. Aguirregabiria and Andrew Duffy
https://dl.dropbox.com/u/44365627/lookangEJSworkspace/export/ejs_users_sgeducation_lookang_dopplerxywee.jar

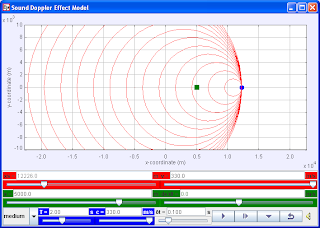Ejs Open Source 1 Dimension Doppler Effect Sound Wave Java Applet

Full screen applet
kindly hosted in NTNUJAVA Virtual Physics Laboratory by Professor Fu-Kwun Hwang
http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=1997.0
alternatively, go direct to http://www.phy.ntnu.edu.tw/ntnujava/index.php?board=28.0
Collaborative Community of EJS (Moderator: lookang) and register , login and download all of them for free :) This work is licensed under a Creative Commons Attribution 3.0 Singapore License
Author: Fu-Kwun Hwang and lookang with ideas by Juan Aguirregabiria and Andrew Duffy

lookang thanks all of them (Fu-Kwun Hwang, Juan M. Aguirregabiria and Andrew Duffy) these are great physics teachers :)

The Doppler effect
The Doppler effect describes the shift in frequency of a wave that is produced by the motion of either the wave source or the observer of the wave (or both).
A sound source is moving with velocity v along the horizontal axis. Every period T a wave front leaves the source and travels with velocity c with respect to a medium (say air), assuming no air motion. A detector is located at position (x, y) and may move with velocity (dx/dt, dy/dt). To promote ease of learning, only the x direction is enabled, thus, making exploration confined to 1 Dimension.
You may change via sliders and edit the values of the aforementioned quantities, as well as the time interval dt between animation frames.
The source and detector position may also be chosen by means of the sliders.
Press Initial to set t = 0 and the source at its initial position.
Press Continue to start or continue the animation.
Press Stop to pause the animation, and Reset to recover the default settings.
In the graphics window below the animation a vertical red (green) bar is displayed each time a wave front leaves the source (reaches the detector).

Activities
Note that the velocities are specified in terms of the wave velocity, where positive is directed right. Thus, a source speed of 1 means that the observer moves at the speed of the waves.

1 Start with the source at rest and the observer at rest, and observe the pattern produced when you press the Play button. Describe the pattern also in terms of the relationship of f and f'. Hint: f = f'
2 Now, keep the source at rest, and give the observer an initial velocity. Explore how the frequency of the waves reaching the observer changes as you vary the observer's velocity. Does this depend on whether the observer is moving toward the source or away from the source? Does the motion of the observer effectively change the speed of the waves or the wavelength?
3 Now, keep the observer at rest and explore the effect of the motion of the source. How does the frequency of the waves reaching the observer depend on the source velocity? Does the frequency shift depend on whether the motion of the source is toward or away from the observer? Does the motion of the source effectively change the speed of the waves or the wavelength?
4 Now that you are more familiar with the simulations terms, objects and quantities, design and experiment to deduce the relationship between f' and f. Hint: a table with your inquiry quantities will be useful in your self directed science discovery.
5 What happens when the source travels at the same speed of the waves? Hint: your explanation should include/ make reference to terms like Mach, Shock-wave, Sound Barrier and Sonic Boom.
6 What happens when the source travels faster than the wave speed? Hint: your explanation should include terms/make reference to Mach, Shock-wave and Supersonic.

Advanced learners! pedagogy of constructionism
7 Use EJs and change the simulation to include 2 dimensions hint: Fu-Kwun Hwang http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=873.0
8. Use EJs and change the simulation to include the reference frame, hint:Andrew Duffy http://www.compadre.org/osp/items/detail.cfm?ID=9982
9 Use EJs and change the simulation to include the effect of wind hint: Juan Aguirregabiria edited by Wolfgang Christian http://www.compadre.org/osp/items/detail.cfm?ID=7902

other Doppler effect ejs applets
EJS version of Doppler effect (You can hear sound) by Fu-Kwun Hwang http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=873.0
Ejs Doppler Effect Model written by Juan Aguirregabiria edited by Wolfgang Christian http://www.compadre.org/osp/items/detail.cfm?ID=7902
Doppler Effect Model written by Andrew Duffy http://www.compadre.org/osp/items/detail.cfm?ID=9982

changes.

add new controls fit my usual design
redrawn for customization to sound Doppler effect v =330 m/s instead of the older 25 m/s
customized to 1 Dimension only
redo the applet on Fu-Kwun Hwang http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=873.0
added visualization of detected and emitted with reference to Ejs Doppler Effect Model written by Juan Aguirregabiria edited by Wolfgang Christian http://www.compadre.org/osp/items/detail.cfm?ID=7902
add sound from Toolkit.getDefaultToolkit().beep(); // taken from http://www.compadre.org/OSP/items/detail.cfm?ID=8385&Attached=1
//Ceiling Bounce Model written by Wolfgang Christian
made the initial v = 170 m/s
made T = 2 s

enjoy!

reference: http://www.physicsclassroom.com/class/waves/u10l3d.cfm
The Doppler effect is observed whenever the source of waves is moving with respect to an observer. The Doppler effect can be described as the effect produced by a moving source of waves in which there is an apparent upward shift in frequency for observers towards whom the source is approaching and an apparent downward shift in frequency for observers from whom the source is receding. It is important to note that the effect does not result because of an actual change in the frequency of the source. Using the simulation above, the source is still producing disturbances such as sound at a rate of f = 0.5 disturbances per second (select T period as 2 second); it just appears to the observer that the source of the wave is approaching say vsource = 170 m/s that the disturbances are being produced at a frequency greater than 0.5 disturbances/second. using the formula f' = f ( c+vobserver) / (c - vsource) = 0.5* ( 330+0)/(330-170) = 1.03 Hz.
when the source is traveling away from the observer, the formula is now formula f' = f ( c-vobserver) / (c + vsource) = 0.5* ( 330-0)/(330+170) = 0.33 Hz.

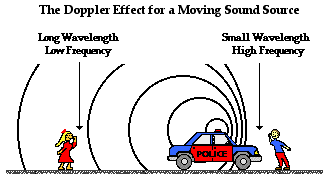http://www.physicsclassroom.com/class/waves/u10l3d3.gif

The Doppler effect can be observed for any type of wave - water wave, sound wave, light wave, etc. We are most familiar with the Doppler effect because of our experiences with sound waves. Perhaps you recall an instance in which a police car or emergency vehicle was traveling towards you on the highway. As the car approached with its siren blasting, the pitch of the siren sound (a measure of the siren's frequency) was high; and then suddenly after the car passed by, the pitch of the siren sound was low. That was the Doppler effect - an apparent shift in frequency for a sound wave produced by a moving source.[img][/img]

The Doppler effect is of intense interest to astronomers who use the information about the shift in frequency of electromagnetic waves produced by moving stars in our galaxy and beyond in order to derive information about those stars and galaxies. The belief that the universe is expanding is based in part upon observations of electromagnetic waves emitted by stars in distant galaxies. Furthermore, specific information about stars within galaxies can be determined by application of the Doppler effect. Galaxies are clusters of stars that typically rotate about some center of mass point. Electromagnetic radiation emitted by such stars in a distant galaxy would appear to be shifted downward in frequency (a red shift) if the star is rotating in its cluster in a direction that is away from the Earth. On the other hand, there is an upward shift in frequency (a blue shift) of such observed radiation if the star is rotating in a direction that is towards the Earth.

reference http://www.kettering.edu/physics/drussell/Demos/doppler/doppler.html

f prime = f ( c + vobserver ) / ( c - vsource) for towards each other (approaching)
f prime = f ( c - vobserver ) / ( c + vsource) for moving away from each other (separating)
codes are:
frequencyemitted = 1/T;
if ((x-xe)*(v0-vobserver) >0){ // towards each other

frequencydetected = frequencyemitted*( v0+ vobserver)/( v0+ vs);
}
else {
frequencydetected = frequencyemitted*( v0- vobserver)/( v0- vs);
}
Or as in Wikipedia,
In classical physics, where the speeds of source and the receiver relative to the medium are lower than the velocity of waves in the medium, the relationship between observed frequency f and emitted frequency f₀ is given by:^[3]

$f = \left( \frac{c \pm v_r}{c \mp v_{s}} \right) f_0 \,$

where

$c \;$ is the velocity of waves in the medium

$v_{r} \,$ is the velocity of the receiver relative to the medium; positive if the receiver is moving towards the source.

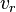$v_{s} \,$ is the velocity of the source relative to the medium; positive if the source is moving away from the receiver.

Read the top signs to use when approaching and bottom signs when separating

Stationary Sound Source

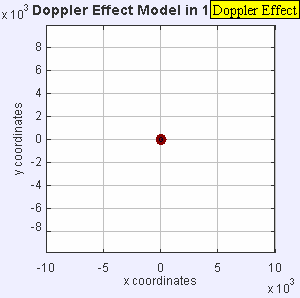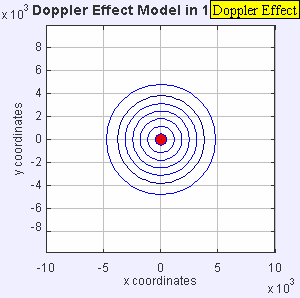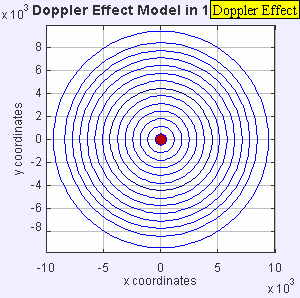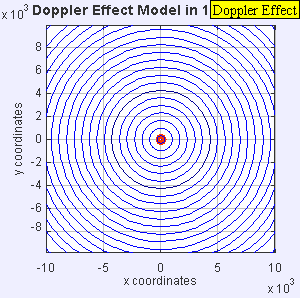Stationary Sound Source

Pasco ripple tank. A small 650W incandescent light source was mounted about one meter above the tank, and the ripples projected on the screen were photographed from the side (see lower picture on the right) using a high-speed video camera by http://livephoto.rit.edu/LPVideos/ripple/

http://livephoto.rit.edu/LPVideos/ripple/Ripple_Tank_Waves_1.mov
click on the link to view the video

Stationary sound source produces sound waves at a constant frequency f, and the wave-fronts propagate symmetrically away from the source at a constant speed c (assuming speed of sound, c = 330 m/s), which is the speed of sound in the medium. The distance between wave-fronts is the wavelength. All observers will hear the same frequency, which will be equal to the actual frequency of the source where

f = f 0

.

Source moving with vsource = 0.7*vsound ( Mach 0.7 )

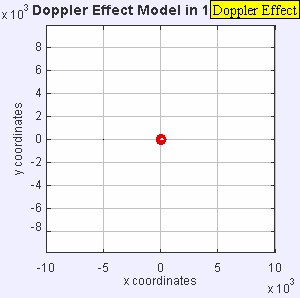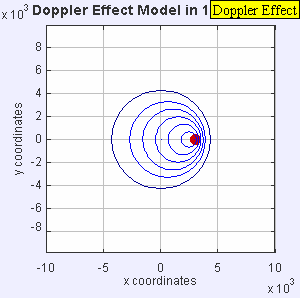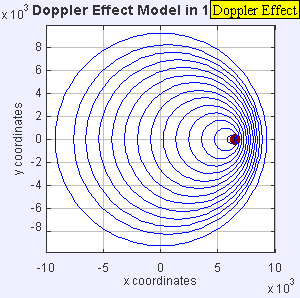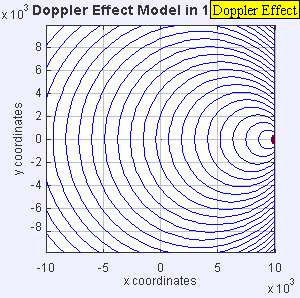Source moving with vsource = 0.7*vsound ( Mach 0.7 )

http://livephoto.rit.edu/LPVideos/ripple/Ripple_Tank_Waves_1.mov
click on the link to view the video on a Doppler effect in ripple tank case by http://livephoto.rit.edu/LPVideos/ripple/

The same sound source is radiating sound waves at a constant frequency in the same medium. However, now the sound source is moving to the right with a speed vs = 0.7 c (Mach 0.7). The wave-fronts are produced with the same frequency as before. However, since the source is moving, the center of each new wavefront is now slightly displaced to the right. As a result, the wave-fronts begin to bunch up on the right side (in front of) and spread further apart on the left side (behind) of the source. 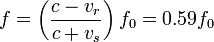An observer in front of the source will hear a higher frequency $f = \left( \frac{c + v_r}{c - v_{s}} \right) f_0 = 3.33f_0\,$ , and an observer behind the source will hear a lower frequency $f = \left( \frac{c - v_r}{c + v_{s}} \right) f_0 = 0.59f_0\,$

Source moving with vsource = vsound ( Mach 1 , breaking the sound barrier )

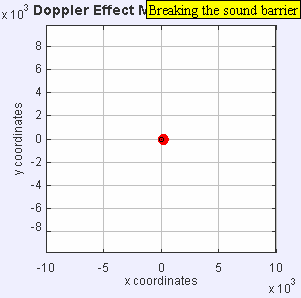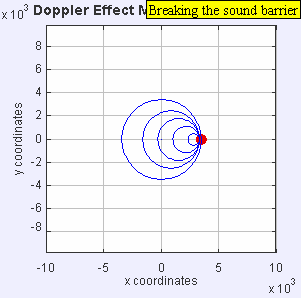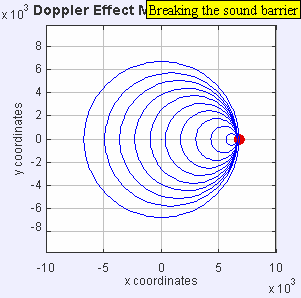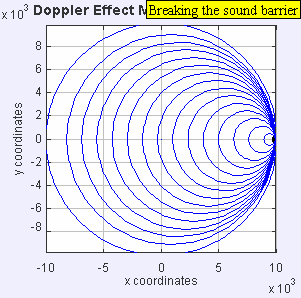Source moving with vsource = vsound ( Mach 1 , breaking the sound barrier )

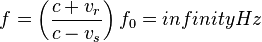Now the source is moving at the speed of sound in the medium (vs = c, or Mach 1). assuming the speed of sound in air at sea level is about 330 m/s . The wave fronts in front of the source are now all bunched up at the same point. As a result, an observer in front of the source will detect nothing until the source arrives where $f = \left( \frac{c + v_r}{c - v_{s}} \right) f_0 = infinity Hz\,$ . 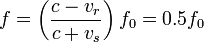An observer behind of the source $f = \left( \frac{c - v_r}{c + v_{s}} \right) f_0 = 0.5f_0\,$ . The pressure front will be quite intense (a shock wave), due to all the wavefronts adding together, and will not be percieved as a pitch but as a "thump" of sound as the pressure wall passes by. The figure at right shows a bullet travelling at Mach 1.01. You can see the shock wave front just ahead of the bullet.

US Navy Photo F/A-18 Hornet passing through the sound barrier. Navy Ensign John Gay made this phenomenal photograph on July 7, 1999 while aboard the carrier USS Constallation as Navy Lt. Ron Candiloro flew by. An MPEG movie of the flyby is also available. http://www.kettering.edu/physics/drussell/Demos/doppler/mach1.html

Every so often, just the right combination of conditions and events occur to create an unbelievable event -- in this case an F/A-18 Hornet passing through the sound barrier. Not only were the water vapor, density and temperature just right, but there just happened to be a camera in the vicinity to capture the moment. Navy Ensign John Gay made this phenomenal photograph on July 7, 1999 while aboard the carrier USS Constallation as Navy Lt. Ron Candiloro flew by.
The plane is actually in transonic flight, with normal shock waves emanating from behind the canopy and across the wings and fuselage. The condition will last for only an instant, and once supersonic flow exists completely around the aircraft, sharp-angled sonic cones replace the normal shock waves.

Source moving with vsource = 1.4*vsound (Mach 1.4 , supersonic)

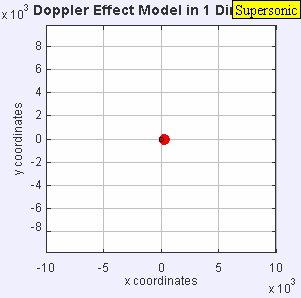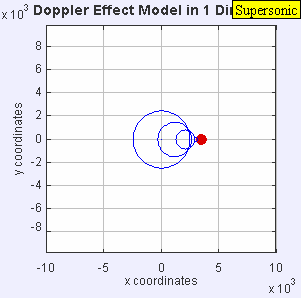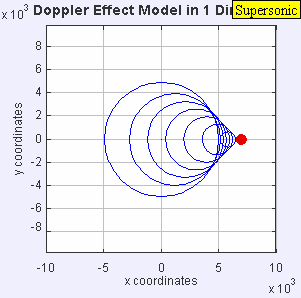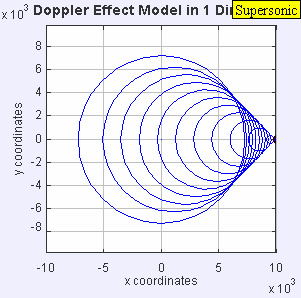Source moving with vsource = 1.4*vsound (Mach 1.4 , supersonic)

The sound source has now broken through the sound speed barrier, and is traveling at 1.4 times the speed of sound, c (Mach 1.4). Since the source is moving faster than the sound waves it creates, it actually leads the advancing wavefront. The sound source will pass by a stationary observer before the observer actually hears the sound it creates. 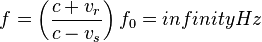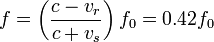As a result, an observer in front of the source will detect $f = \left( \frac{c + v_r}{c - v_{s}} \right) f_0 = infinity Hz\,$ and an observer behind the source $f = \left( \frac{c - v_r}{c + v_{s}} \right) f_0 = 0.42f_0\,$ .

As you watch the animation, notice the clear formation of the Mach cone, the angle of which depends on the ratio of source speed to sound speed. It is this intense pressure front on the Mach cone that causes the shock wave known as a sonic boom as a supersonic aircraft passes overhead. The shock wave advances at the speed of sound v, and since it is built up from all of the combined wave fronts, the sound heard by an observer will be quite intense. A supersonic aircraft usually produces two sonic booms, one from the aircraft's nose and the other from its tail, resulting in a double thump.

bullet traveling at Mach 2.45. http://www.kettering.edu/physics/drussell/Demos/doppler/bullet-3.gif

The figure at right shows a bullet traveling at Mach 2.45. The mach cone and shock wave-fronts are very noticeable.

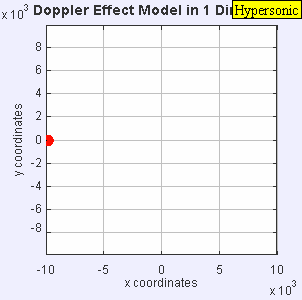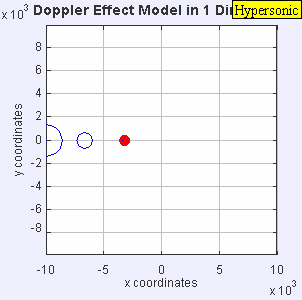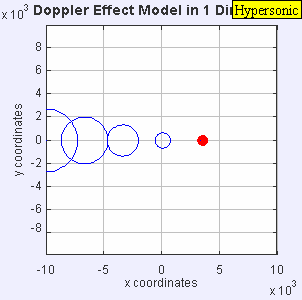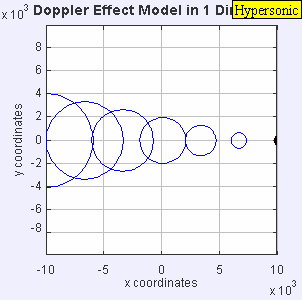slow motion of a hypersonic motion Mach = 5.0

Contribution to wikimedia as an active citizen of the world

Date	Name	User	Size	Description
15:56, 24 September 2011	Dopplereffectsourcemovingrightatmach5.0.gif (file)	Lookang	545 KB	(change text to hypersonic)
15:44, 24 September 2011	Dopplereffectsourcemovingrightatmach1.4.gif (file)	Lookang	214 KB	(supersonic text, dt =0.5)
15:36, 24 September 2011	Dopplereffectsourcemovingrightatmach1.0.gif (file)	Lookang	332 KB	(dt = 0.5)

Thumbnail	Date	Name	User	Size	Description
	09:14, 12 September 2011	Dopplereffectsourcemovingrightatmach5.0.gif (file)	Lookang	542 KB

Date	Name	User	Size
07:23, 12 September 2011	Dopplereffectsourcemovingrightatmach1.4.gif (file)	Lookang	213 KB
07:23, 12 September 2011	Dopplereffectsourcemovingrightatmach0.7.gif (file)	Lookang	568 KB
07:23, 12 September 2011	Dopplereffectstationary.gif (file)	Lookang	534 KB
07:23, 12 September 2011	Dopplereffectsourcemovingrightatmach1.0.gif (file)	Lookang	330 KB