Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits

 Lee Tat Leong slightly remixed by lookang (This email address is being protected from spambots. You need JavaScript enabled to view it.); This email address is being protected from spambots. You need JavaScript enabled to view it.
Lee Tat Leong slightly remixed by lookang (This email address is being protected from spambots. You need JavaScript enabled to view it.); This email address is being protected from spambots. You need JavaScript enabled to view it.
end faq
Apps

https://play.google.com/store/apps/details?id=com.ionicframework.atwoodmachineapp294376&hl=en
Problem Statement/Description:
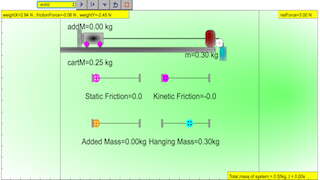
An Atwood’s machine consists of two masses tied together using a massless non-elastic string hung over a massless frictionless pulley. Using data acquired from a simple Atwood’s machine, graphically determine the earth’s gravitational acceleration. For this experiment, we will keep the total mass of the system (M + m) constant.
Equipment depending on resources available and degree of blending real and virtual, best to do Real and then Virtual later.
- Option 2: Real: stopwatch, pulley, string, meter- rule, 2 x slotted masses (350g + 2 x 10g + 2 x 5g), retort stand, mat to absorb the impact of falling masses
- Option 1: Computer/ Handphone App: https://play.google.com/store/apps/details?id=com.ionicframework.atwoodmachineapp294376&hl=en
- Option 3: ICT: stopwatch, pulley, string, meter- rule, 2 x slotted masses (350g + 2 x 10g + 2 x 5g), retort stand, mat to absorb the impact of falling masses and including a photogate (smart pulley) and datalogger
Safety Consideration
- If the difference between the masses on each hanger is too great, the masses may fly off the pulley and hanger when released. For this experiment, use values of M - m (Δm) in the range of 10g – 60g.
- Make sure that the coast is clear before releasing the mass and do not squat right under the masses as there is a chance that the string holding the masses might break. Place the mat directly below the falling mass m2 to absorb the impact of the fall, while also making sure that mass M does not hit the pulley as m hits the mat.
Related Concepts
- Newton’s 2nd law, acceleration of free fall, the 1D motion of uniformly accelerated objects, the principle of conservation of energy
Pre-Lab Discussion
- You may be familiar with drawing free body diagrams and forces acting on common objects like blocks sliding down inclines, objects falling through the air, and other projectiles we often treat as point masses. But what about a free body diagram for an awkward shape? This lab pertains to a system called an Atwood machine that can be modeled with a free body diagram if we treat the entire system as one accelerating object.
- Show that by applying Newton’s second law for the entire system, we obtain Eq. 1:
\( a = \frac{mg - \mu (M+M_{add})g}{M+M_{add}+m} \)
m is the hanging mass
g is the gravitational acceleration
μ is the coefficient of friction
M is the mass of the cart - Madd is the mass added to the cart
Why is the tension in the string not a factor in the above equation?
- Note that the torque required to cause the pulley to begin spinning is assumed to be negligible, as is the mass, friction, and rotational inertia of the pulley.
Design and Conduct the Experiment
- What variables from Eq. 1 can be measured directly using equipment from the materials list above? What piece of equipment will you use to measure each variable?
- What variables will you change to get at least 5 different data points for the acceleration of the system? What variables must remain constant in order to get a consistent graph of acceleration?
- If you move masses from the rising hanger to the falling hanger, will this change the total system mass? Explain why or why not.
- What types of acceleration will you observe as the mass difference becomes greater between the two hangers?
- Describe the potential sources of errors that could prevent you from gathering accurate consistent data.
- Give a short description of the procedure you will use, identifying what measurements you will make, the points at which you will make these measurements, and how each piece of equipment will be used to make these measurements.
Sample Learning Goals
Investigate the relationship between the mass and the acceleration of the system
- keep the external force (hanging mass) constant
- add mass to the cart
Equations
The Atwood machine (or Atwood's the machine) was invented in 1784 by the English mathematician George Atwood as a laboratory experiment to verify the mechanical laws of motion with constant acceleration. Atwood's machine is a common classroom demonstration used to illustrate principles of classical mechanics.
The idea frictionless Atwood Machine consists of two objects of mass (Mass of cart M plus additional mass added Madd ) and m (hanging mass), connected by an inextensible massless string over an ideal massless pulley. [1]
When M+Madd = m, the machine is in neutral equilibrium or net force is equal to zero, regardless of the position of the weights.
When M+Madd ≠ m the system of masses experience uniform acceleration.
We are able to derive an equation for the acceleration by using force analysis or free body diagram. If we consider a massless, inextensible string and an ideal frictionless pulley.
As a sign convention, we assume that a is positive when downward for the mass m and to the right for M+Madd
By considering free body diagram of M+Madd we get
F = ma
T - f = (M+Madd)a
where
T is the tension pointing towards the right on the cart and added mass system
f is the friction force on the cart and added mass system on the wheels (assume to be a single force pointing left, thus the minus sign)
a is the acceleration of the cart and added mass system
Similarly, by considering the free body diagram of the hanging mass
F = ma by continuous motion, downwards as positive,
mg - T = ma
by substitution,
T = (M+Madd)a +f =mg -ma
we get
\( a = \frac{mg - f}{M+M_{add}+m} \)
to get an equation of removing f, consider the forces of the cart and added the mass system in the vertical direction
F = ma
R - (M+Madd) g = 0
in addition, the frictional model is related by this equation
f ≤ μR
in motion, assume f = μR
therefore, the equation of acceleration can be simplified to
\( a = \frac{mg - \mu R}{M+M_{add}+m} \)
\( a = \frac{mg - \mu (M+M_{add})g}{M+M_{add}+m} \)
m is the hanging mass
g is the gravitational acceleration
μ is the coefficient of friction
M is the mass of the cart
For Teachers
This simulation is to recreate Walter Fendt's Newton's Second Law applet (http://www.walter-fendt.de/ph14e/n2law.htm). The purpose is to align with Modelling Instructions approach to formulate F = ma with the experiment conducted with motion sensor rather than the light gate.
 |
| example data set collected across varying m from 0.30 to 0.50 kg which results in increasing amount of curve in the parabolic of the model form, x = x0 + vo*t +0.5*a*t^2Modified Atwood Machine JavaScript HTML5 Applet Simulation Model by Tat Leong Lee and Loo Kang Wee |
 |
| example data set collected across varying addM from 0 to 0.30 kg which results in decreasing amount of curve in the parabolic of the model form, x = x0 + vo*t +0.5*a*t^2 Modified Atwood Machine JavaScript HTML5 Applet Simulation Model by Tat Leong Lee and Loo Kang Wee |
6.4 Dynamics: Map of key concepts and ideas covered at upper secondary level Motion of objects Key inquiry question:
Why do objects on Earth and in the Universe move the way they do?
1. Mass, weight, and density
• Mass is a measure of the amount of substance in a body. A body’s mass resists a change in the state of rest or motion of the body (inertia).
• The density of a substance is the mass per unit volume of the substance i.e. density = mass/volume (ρ = m/V). Density can be measured as the mass of 1 cm3 of any substance.
• Mass, a measure of the amount of substance in an object has magnitude only (scalar), whereas weight, which is the force acting on a body in a gravitational field, has both magnitude and direction (vector).
• Using Newton’s 2nd law, Force = mass x acceleration; Weight = mass x acceleration due to gravity (or gravitational field strength) (W = mg).
2. Newton’s laws of motion
• Newton’s Laws of motion may be applied to: describe the effect of balanced and unbalanced forces on a body; describe the ways in which a force may change the motion of a body, and identify action-reaction pairs acting on two interacting bodies.
• Newton’s 1st law states that an object remains at rest or continues with constant speed in a straight line when no resultant force acts on it (no resultant force means that all the forces acting on the object are balanced). • Newton’s 2nd law states that the resultant force on a body = the mass of the body x acceleration of the body (F = ma). The direction of the acceleration is the same as the direction of the resultant force acting on the body.
• Newton’s 3rd law states that the forces of two bodies on each other (action-reaction pair) are always equal and act along the same line in opposite directions. The two forces (action-reaction pair) are of the same type. Force always appears in a pair. The existence of a single force is impossible.
3. Free-body diagrams
• Free-body diagrams and vector graphical diagrams may be used to represent and analyze the forces acting on a body.
• A free-body diagram shows the forces acting on a body only, not the forces the body exerts on other bodies.
• The resultant force acting on the body can be found using graphical methods (parallelogram method or ‘head-to-tail’ method).
Students’ prior knowledge of Dynamics and Gravitational field
Primary level:
Students learn about mass (a measure of the amount of matter in a body) and volume (the amount of space that a body occupies) and the use of appropriate apparatus to measure these quantities (e.g. use of a lever balance, an electronic balance, a measuring cylinder, a syringe, and a measuring jug). However, the concept of density is not introduced although students do simple experiments to investigate the ability of objects of different materials (plastics, wood, rubber, and metals) to float/sink in water.
Students recognize that objects have weight because of the gravitational force between them and the Earth and that weight is different at different places and can be measured using a spring balance or a weighing scale.
Lower secondary level:
Students learn that:
• the density of a substance is the mass of the substance per unit volume and can be used to predict whether objects sink or float.
• gravity exists between any two objects (e.g. ball and Earth). The weight of an object depends on the force of gravity pulling on that object. Students’ common misconceptions and learning difficulties in Dynamics and Gravitational field
Newton’s first law:
Students often think that:
• a force is required to maintain an object in its motion;
• if there is no motion, there is no force acting;
• constant speed results from a constant force;
• friction (instead of inertia) causes objects to resist a change in its state of rest or motion.
Newton’s second law:
Students often think that:
• a larger velocity means a larger resultant force;
• acceleration implies increasing force;
• greater mass implies greater force;
• a force cannot move an object unless it is greater than the object’s weight;
• heavier objects fall faster than light objects.
Newton’s third law:
Students often think that force is a single physical quantity associated with a single object rather than as an interaction between two objects which must, therefore, exist as an action-reaction pair. They have difficulty in understanding that:
• two objects of greatly differing masses (e.g. Earth and us) exert forces of equal magnitude on each other;
• the normal force on an object and the weight of the object do not always have equal magnitudes;
• gravity acts on an object all the time (not just when it is falling).
Analysis
Present your data in the form of a labeled graph with the corresponding data table, or any other way you find useful to graphically determine the earth's gravitational acceleration g.
- Δm represents the difference in mass that led to the acceleration of the system. Draw a free body diagram with the forces acting on the system.
- Use your graph of acceleration versus Δm to determine an experimental value for g. Explain the procedure you used to determine this value.
- Should your graph pass through the origin (0, 0)? Would you consider (0,0) as an experimental point?
- Calculate the % difference in your experimental value for g.
- What graph would you plot to verify Newton’s second law? How can you tell from your graph that your data supports Newton’s second law?
- How would the accelerations you measured in this lab change if you were still moving the same small masses from one hanger to the other for each trial, but the total mass of the system was much larger?
- For low acceleration values, how would the mass and friction of the pulley affect the values for g? Would they be erroneously high or low? Explain your answer.
- For high values of acceleration, the string may actually slip on the pulley wheel. How would this error affect the observed values for system acceleration?
Extension - Modified Atwood Machine
- Vary the acceleration of the block by changing the mass on the hanger – verify Newton’s second law
- How can we tell if friction between the block and the table is significant? If so, how can we experimentally determine its value, without the help of the smart pulley system and datalogger? (Hint: You will not need to use a stopwatch; just use energy considerations.)
Video
https://youtu.be/lagGL0catfI by Nawal Nayfeh
Worksheets
Version:
- https://weelookang.blogspot.com/2024/03/exploring-physics-with-modified-atwood.html
-
http://weelookang.blogspot.sg/2016/08/modified-atwood-machine-javascript.html
-
http://weelookang.blogspot.sg/2013/04/ejs-open-source-modified-atwood-machine.html
Other Resources
- http://www.walter-fendt.de/html5/phen/newtonlaw2_en.htm JavaScript version by Walter Fendt
- http://www.walter-fendt.de/ph14e/n2law.htm
- http://lectureonline.cl.msu.edu/~mmp/kap4/cd097a.htm
- https://www.geogebra.org/m/hh9CGse3#material/K6afWTwQ
- https://www.geogebra.org/m/ztUKm6QV Moment of Inertia: Rolling and Sliding Down an Incline by ukukuku
- The Atwood machine revisited using smartphones