Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits


 Francisco Esquembre; Flix J. Garca Clemente; Loo Kang WEE
Francisco Esquembre; Flix J. Garca Clemente; Loo Kang WEE
end faq
Sample Learning Goals Procedure
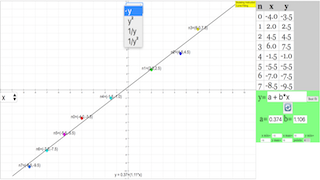
This model fits a polynomial curve to a data set. Users can add points (up to a limit) by clicking within the plotting panel. Add data to the panel and then adjust the parameters of the polynomial y = f(x), in order to obtain a good fit using the a,b,c,d, and e parameters. Use the best fit button to compare your fit to the the best possible polynomial fit.
NumericJS model element
This model demonstrates how to use theNumeric JSmodel element (see theElementspanel of the model) to solve the system of linear equations required for the least squares approximation.
Reference:Least Squaresentry of theWikipedia.
For Teachers Curve Data Fitting
The objective of this model is to fit a curve to a number of points. You can add points (up to a limit) by clicking on the panel.
Your task is to adjust the parameters of the curve y = f(x), (or the functionf(x)itself!) in order to obtain the best possible fit. You have up to 5 parameters,a,b,c,d, and e.
Edit the "computeBestFit()" method in theCustompanel of the model to edit your best fit algorithm. Then, click on the "Best Fit" button, each time it is displayed in red, to invoke this method.
NumericJS model element
This model uses theNumeric JSmodel element (see theElementspanel of the model) to help you solve the system of linear equations required for the least squares approximation.
Reference: Least Squares entry of the Wikipedia.
Our function is
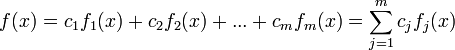
where{fj(x)}are a basis of linear independent functions:{1,x,x2,x3,...,xm}and{cj}are the coefficients.
The objective is to minimize the sum:
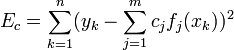 .
.
To this end, we have to differentiate with respect toci, and equate to zero:
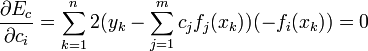
Obtaining the follow system:
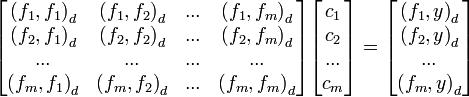
where (a,b)dare defined as:
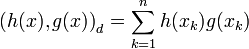 .
.
Research
[text]
Video
[text]
Version:
- http://weelookang.blogspot.sg/2016/06/data-fitting-javascript-html5-applet.html
- http://www.opensourcephysics.org/items/detail.cfm?ID=13350 original simulation by Francisco Esquembre and Miguel Marín López
Other Resources
[text]