About
Vector Addition, and Drawing Patterns
This simulation illustrates the tail-to-tip method of adding vectors.
The table at the bottom shows the components and lengths of the vectors.
You can also rotate the vectors and trace out some interesting patterns.
Activities
- Given the magnitude and angles of the two vectors, do you agree with the values shown for the components of the three vectors in the table at the bottom? Explain how the components are determined.
- For a given pair of vectors, how do you find the maximum possible magnitude of their resultant vector? How do you determine the minimum possible magnitude?
- By changing the orientation of one or both of the vectors, can you obtain a resultant vector with any magnitude between the minimum and maximum value
- Adjust the lengths of the two vectors and their rotation rates, and then hit Play. See what kind of interesting patterns you can make, just by adding vectors.
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits

 Andrew Duffy; Loo Kang Wee
Andrew Duffy; Loo Kang Wee
end faq
Sample Learning Goals
AAAS Benchmark Alignments (2008 Version)
11. Common Themes
- 9-12: 11B/H2. Computers have greatly improved the power and use of mathematical models by performing computations that are very long, very complicated, or repetitive. Therefore, computers can reveal the consequences of applying complex rules or of changing the rules. The graphic capabilities of computers make them useful in the design and simulated testing of devices and structures and in the simulation of complicated processes.
For Teachers
|
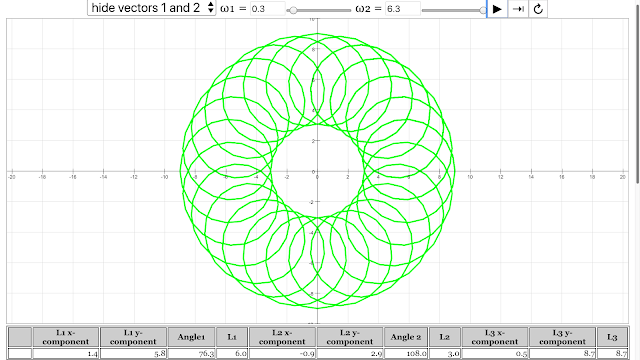
The pattern of coil emerged from angular velocity of vector 1 = 0.3 rad/s, angular velocity of vector 2 = 6.3 rad/s Vector Addition Pattern Creativity Lesson JavaScript HTML5 Applet Simulation Model by Andrew Duffy and Loo Kang Wee |
|
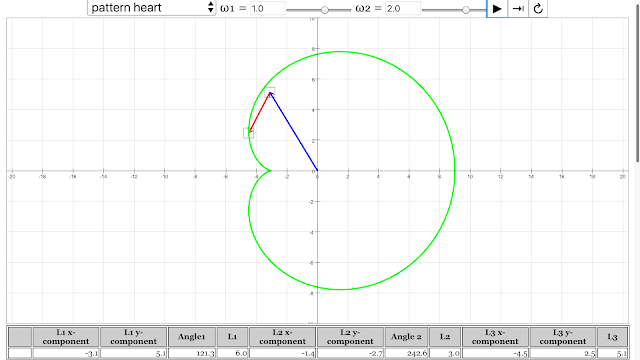
The pattern of heart emerged from angular velocity of vector 1 = 1 rad/s, angular velocity of vector 2 = 2 rad/s Vector Addition Pattern Creativity Lesson JavaScript HTML5 Applet Simulation Model by Andrew Duffy and Loo Kang Wee |
|
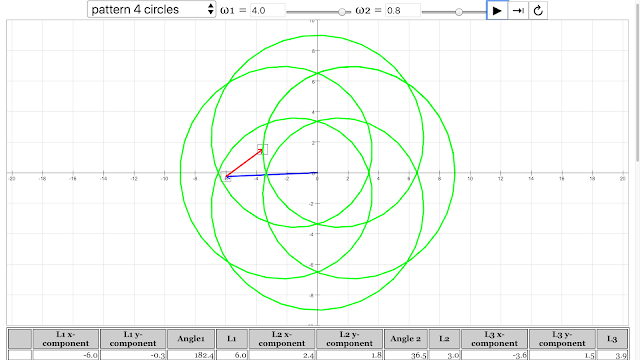
The pattern of 4 circles emerged from angular velocity of vector 1 = 4 rad/s, angular velocity of vector 2 = 0.8 rad/s Vector Addition Pattern Creativity Lesson JavaScript HTML5 Applet Simulation Model by Andrew Duffy and Loo Kang Wee |
|
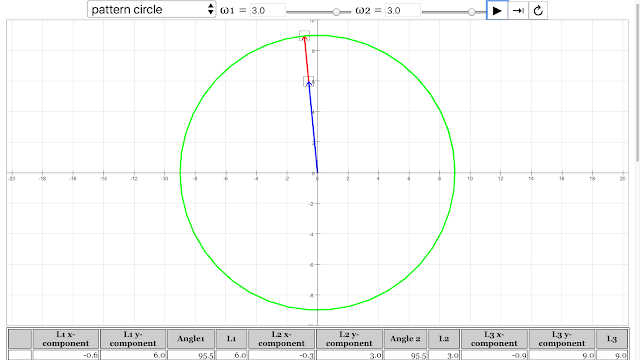
The pattern of circle emerged from angular velocity of vector 1 = 3 rad/s, angular velocity of vector 2 = 3 rad/s Vector Addition Pattern Creativity Lesson JavaScript HTML5 Applet Simulation Model by Andrew Duffy and Loo Kang Wee |
|
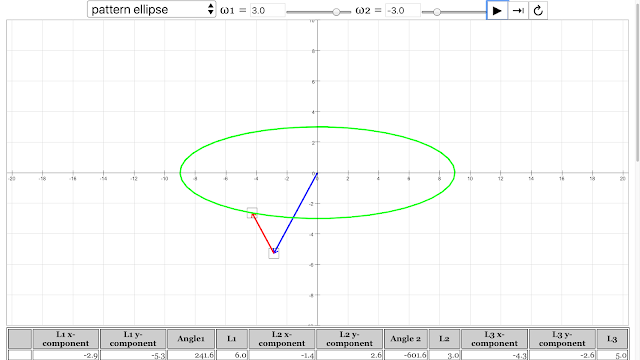
The pattern of ellipse emerged from angular velocity of vector 1 = 3 rad/s, angular velocity of vector 2 = -3 rad/s Vector Addition Pattern Creativity Lesson JavaScript HTML5 Applet Simulation Model by Andrew Duffy and Loo Kang Wee |
|
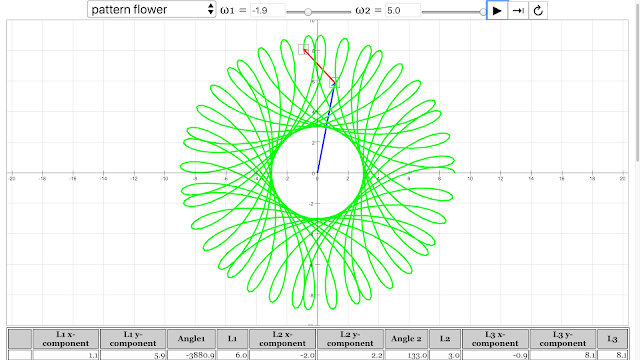
The pattern of flower emerged from angular velocity of vector 1 = -1.9 rad/s, angular velocity of vector 2 = 5 rad/s Vector Addition Pattern Creativity Lesson JavaScript HTML5 Applet Simulation Model by Andrew Duffy and Loo Kang Wee |
Research
[text]
Video
[text]
Version:
- https://weelookang.blogspot.com/2019/01/vector-addition-pattern-creativity.html
- https://www.compadre.org/osp/items/detail.cfm?ID=10011
- http://physics.bu.edu/~duffy/Ejs/EP_chapter01/vector_addition_sim2_v4.html

.png
)