Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits

 This email address is being protected from spambots. You need JavaScript enabled to view it.; Lye Sze Yee
This email address is being protected from spambots. You need JavaScript enabled to view it.; Lye Sze Yee
end faq
Apps
https://play.google.com/store/
https://itunes.apple.com/us/
Description
Momentum One Dimension Collision Model
The motion of a body of mass m and velocity v is described by a vector quantity known as momentum p where
p = m v
When objects collide, whether trains, cars, billiard balls, shopping carts, or your foot and the sidewalk, the results can be complicated. Yet even in the most chaotic of collisions, as long as there are no net external forces acting on the colliding objects, one principle always holds and provides an excellent tool for understanding the collision. That principle is called the conservation of linear momentum which states that
The total momentum of a system remains constant provided that no external resultant force acts on the system
For two bodies colliding linearly, it is written mathematically as a vector equation
Total initial momentum = total final momentum
m1.u1 + m2.u2 = m1.v1 + m2.v2
If external forces (such as friction) are ignored, the total momentum of two carts prior to a collision (left side of equation) is the same as the total momentum of the carts after the collision (right side of equation).
Collisions are classified into elastic (or perfectly elastic), inelastic and completely inelastic.
There is also a concept of kinetic energy of a moving body is stated mathematically by the following equation:
KE1 = ½ m1.v12
Main Simulation View
The simulation has 2 collision carts on frictionless floor and wheels.
Sliders
Explore the sliders allows varying the variables .
* mass of cart ONE, mass_1, m1 in kg
* initial velocity of cart ONE, u1 in m/s
* mass of cart TWO, mass_2, m2 in kg
* initial velocity of cart TWO, u2 in m/s
DropDown Menu
Allows for selecting what kind of collision is simulated.
A Perfectly elastic collision is defined as one in which both conservation of momentum and conservation of kinetic energy are observed
A Perfectly Inelastic collision is defined as one in which conservation of momentum is observed but the colliding carts stick together after collision with kinetic energy loss
DropDown Menu
show: velocity, for visualizing the velocity vector
plot momentum vs time graph, for different representation of data for momentum of cart 1, 2 and both.
plot kinetic energy vs time graph, for different representation of data for kinetic energy of cart 1, 2 and both.
hint: COM, for the equation of conservation of momentum
hint: COKE, or the equation of conservation of kinetic energy
Buttons
Play
Step Forward
Reset
have their usual meaning.
Credits:
The Momentum 1D JavaScript Collision model was created by created by lookang using the Easy Java Simulations (EJS) version 5.2 authoring and modeling tool. Shout our thanks to the Ejs community namely, Francisco Esquembre, Félix J. García Clemente , Fu-Kwun Hwang and Wolfgang Christian for their professional learning community support. You can examine and modify this compiled EJS model if you run the model (double click on the model's jar file), right-click within a plot, and select "Open EJS Model" from the pop-up menu. You must, of course, have EJS installed on your computer. Information about EJS is available at: http://www.um.es/fem/Ejs/ and in the OSP comPADRE collection http://www.compadre.org/OSP/.
Video
Astro Academy: Principia - Collisions by National Space Academy
Ejs open source java applet 1D collision carts Elastic and Inelastic Collision by lookang lawrence wee
Ejs open source java applet 1D collision carts Elastic and Inelastic Collision v2 by lookang lawrence wee
https://www.facebook.com/AskMencom/videos/10153205007388723/
Screenshots
Student Learning Space Force vs Time Collision Carts JavaScript HTML5 Applet Simulation Model
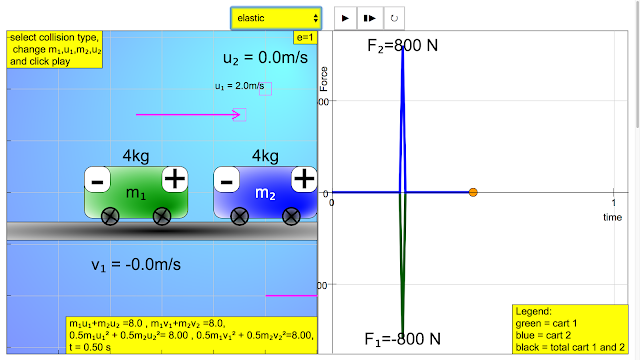 |
| Student Learning Space Force vs Time Collision Carts JavaScript HTML5 Applet Simulation Model Elastic collision results in a large contact force F1 is -800 N that points to the left acting on m1, F2 is 800 N points to the right on the mass m2 http://iwant2study.org/ospsgx/index.php/586 |
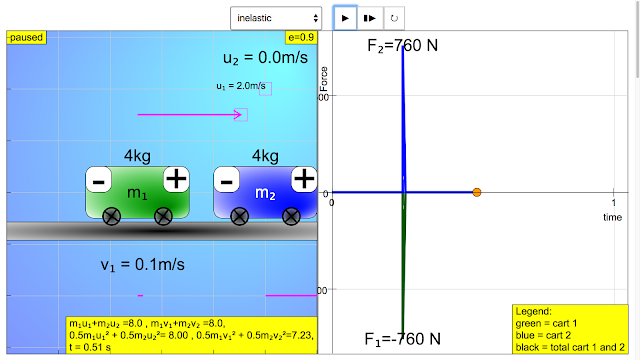 |
| Student Learning Space Force vs Time Collision Carts JavaScript HTML5 Applet Simulation Model a randomly generated (in this case e = 0.9) inelastic collision results in a large contact force F1 is -760 N that points to the left acting on m1, F2 is 760 N points to the right on the mass m2 http://iwant2study.org/ospsgx/index.php/586 |
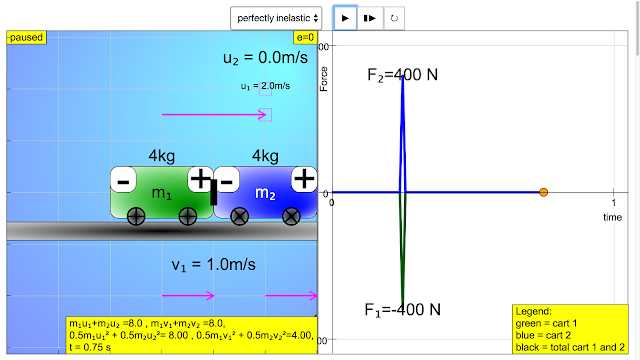 |
| Student Learning Space Force vs Time Collision Carts JavaScript HTML5 Applet Simulation Model Perfectly inelastic collision results in a large contact force F1 is -400 N that points to the left acting on m1, F2 is 400 N points to the right on the mass m2 http://iwant2study.org/ospsgx/index.php/586 |
Worksheets
- Momentum1D01momAJCPBI Worksheet_Dynamics_2012_final.docx
- Momentum1D01momAJCPBI Worksheet_Dynamics_2012_final_soln.docx
- Momentum1D01momIJCMomentum_worksheet_v1.6_lab_worksheet_IJC1.doc
- Momentum1D01momIJCMomentum_worksheet_v1.6_lab_worksheet_IJC2.doc
- Momentum1D01momRVHSP06 EduLabs (st).doc
- Momentum1D01momRVHSP06 EduLabs v3 (tr).docx
- Momentum1D01momSRJCLessonPlan.docx
- Momentum1D01momSRJCMomentum_worksheet_control_teacher-led.doc
- Momentum1D01momSRJCMomentum_worksheet_experimental.doc
- Momentum1D01momSRJCPre- and Post-test (final).docx
- Momentum1D01momYJC2016 JC1 H1 Phy HBL (teacher) - Collision Carts Model.pdf
- Momentum1D01momYJCPWS 7 - Understanding Newton's 3rd law & COM using EJS (Student).doc
- Momentum1D01momYJCPWS 7 - Understanding Newton's 3rd law & COM using EJS (Teaching notes).doc
- ejss_model_Momentum1D0104.Dynamicsofcollision.WorksheetIJCFangFang.docx.docx
Versions
- http://weelookang.blogspot.sg/2018/01/student-learning-space-force-vs-time.html SLS version collaboration with Chai Seng
- http://weelookang.blogspot.sg/2013/09/one-dimension-collision-js-model.html JavaScript version of EJSS One Dimension Collision JS Model by
- http://weelookang.blogspot.sg/2012/02/ejs-open-source-collision-carts-model.html Java version of the Ejs Open Source Collision Carts Model with AJC and RVHS
- http://iwant2study.org/lookangejss/02_newtonianmechanics_3dynamics/ejs/ejs_model_Momentum1DForceModel09.jar Java version of simulation on Digital Library
Research
- arXiv:1204.4964 [pdf, other]
One-dimensional collision carts computer model and its design ideas for productive experiential learningComments: 6 pages, 8 figures, 1 table, 1 L. K. Wee, Physics Education 47 (3), 301 (2012); ISSN 0031-9120Journal-ref: Physics Education, 47(3), 301 (2012)Subjects: Physics Education (physics.ed-ph); Classical Physics (physics.class-ph); Computational Physics (physics.comp-ph)
Other Resources
- http://www.walter-fendt.de/html5/phen/collision_en.htm Collision Carts by Walter Fendt
- http://www.physicsclassroom.com/Physics-Interactives/Momentum-and-Collisions/Collision-Carts Collision Carts by Physicsclassroom
- http://weelookang.blogspot.sg/2014/11/ejss-collision-model-by-dave-lommen.html EJSS collision model by Dave Lommen
- http://weelookang.blogspot.sg/2014/07/ejs-1d-collision-model-with-virtual.html EJS 1D collision model with virtual spring model by Fu-Kwun Hwang and Loo Kang Wee
- https://phet.colorado.edu/en/simulation/collision-lab Collision Lab by PhET
- http://www.mrmont.com/games/carcollision.html
- http://www.opensourcephysics.org/items/detail.cfm?ID=14162 International Space Station: Collisions Video Analysis with Tracker by Tim Peake, Robin Mobbs, Anu Ojha, Andy McMurry, and Sophie Allan
- https://www.geogebra.org/m/n3X5njnT Elastic & Inelastic Collisions by ukukuku
- https://www.geogebra.org/m/gSmRe62s The Ballistic Pendulum by ukukuku
- https://www.geogebra.org/m/Ks939X8m Conservation of Momentum and Energy by ukukuku

.png
)





