About
7.3 Gravitational Potential Energy (symbol: U and units: J)
7.3.1 in Work, Energy & Power topic
In the topic of Work, Energy & Power, the calculation of gravitational potential energy (GPE) is determined using the expression, mgh, which assumes that the gravitational field strength g is roughly constant, but a more robust formula is required for varying field strength, say when sending rockets which travel into outer space from the surface of the Earth.
ΔU = ΔPE = mgh or mgΔh
where ΔPE or ΔU is the gravitational potential energy possessed by mass m measured from the reference height h0 , g is the gravitational field strength created by source mass M.
h or Δh is the change in the height (h1 - h0 ) of the mass m.
7.3.2 more universal formula for Potential energy
This formula PE = mgh or mgΔh was appropriate when the magnitude of gravitational field strength, g of Earth was assumed to be constant (9.81 m s-2) over this height. When the assumption of constant gravitational field strength is not valid, a more robust PE formula is given by the calculation of potential energy
where
U is the gravitational potential energy possessed by mass m measured from the reference position of infinity,
G is the gravitational constant, approximately 6.673×10−11 N·(m/kg)2,
M is the source mass that sets up the gravitational field,
m is the test mass experiencing the gravitational field set up by M, and
r is the distance away from the centre of the gravitational field source mass M
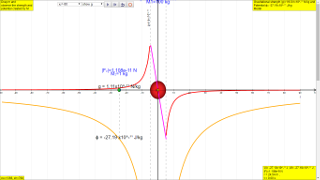
In this particular case,
Calculate for the case when r = 50 m.
Similarly,
7.3.3 Characteristics of Gravitational potential energy
equation is given bya scalar quantity (i.e. it has no direction only magnitude )
has only negative value due to the reference potential equal zero U = 0, position is defined at position r = infinity, ∞, and gravity is attractive which means the lowest potential position is at the centre of the source mass M.
U = -infinity, at r = 0, lowest potential energy
U = 0, at r = infinity, highest potential energy
Now, this leads to the need to define gravitational potential energy.
7.3.4 Definition of gravitational potential energy, U
The gravitational potential energy (U) of a mass m at a point (due to the gravitational field set up by mass M ) is defined as the work done by an external agent in bringing the mass from infinity to that point r distance away from source mass M.To further understand the meaning of this definition, let's start with the definition for work done on external agent, where WD = WD by external agent.
Substituting the formula for force F and working out the integration, it can be shown.
Notice the formula for this work done by external agent is equal to the U.
To understand this definition, we can use the simulation with some imagination.
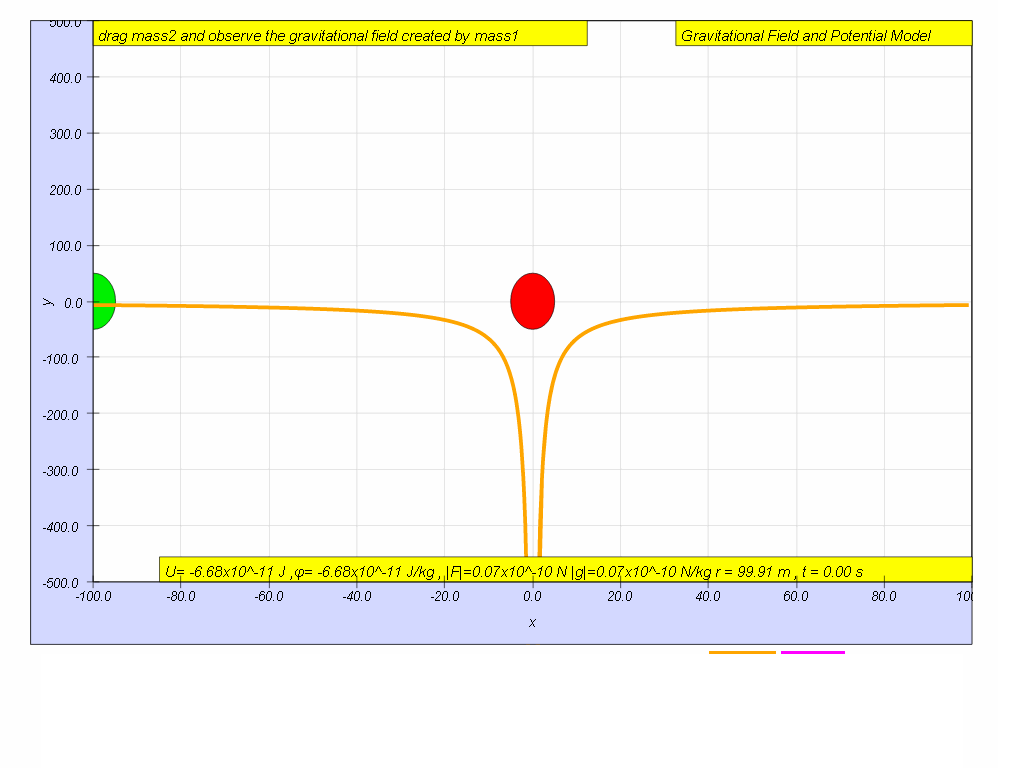
Imagine the test mass, m is at a distance r = ∞, U∞ = 0 (the simulation does not allow r = ∞, but let's assume r = 100 is somewhat far enough)
Let imagine a force pointing towards infinity away from source mass M, acting on this test mass m, the potential energy of m at this point would be therefore the work done by this external force.
WD= Ufinal-Uinitial=Ur-U∞
which means that the work done by external force is equal to the gravitational potential energy (Ur) since U∞ = 0.7.3.5 Suggested activity
The intent of these activities is to allow students be like a student-scientists and collect their own data to form an understanding of potential energy.
The test mass (green) is at r = 100 m, observe and record the value for U r=100 = -6.67 x10-11 J
Click play and pause the model when r = 90 m, record the value of U r=90 = ____________ J
Click play and pause the model when r = 80 m, record the value of U r=80 = ____________ J
Click play and pause the model when r = 70 m, record the value of U r=70 = ____________ J
Click play and pause the model when r = 60 m, record the value of U r=60 = ____________ J
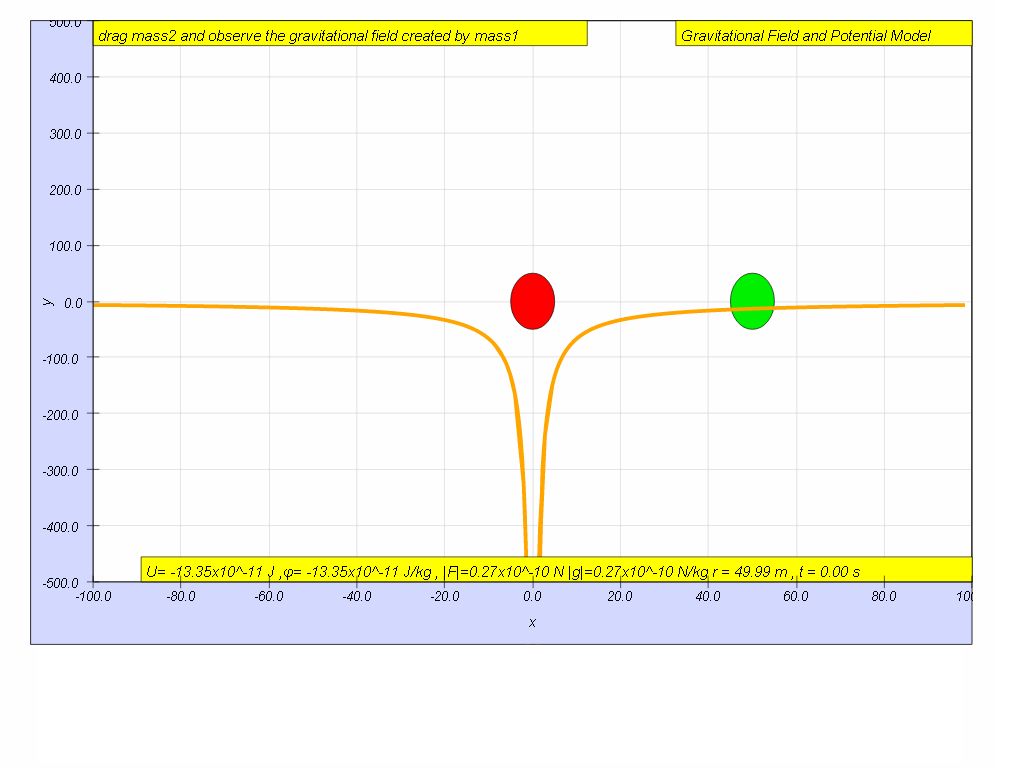
Click play and pause the model when r = 50 m, record the value of U r=50 = ____________ J
Click play and pause the model when r = 40 m, record the value of U r=40 = ____________ J
Click play and pause the model when r = 30 m, record the value of U r=30 = ____________ J
Click play and pause the model when r = 20 m, record the value of U r=20 = ____________ J
Calculate the change in U from r = 100 to r = 50.
Answer is about
Check the "your model" checkbox and a teal color line appear. For example if the model is , , key in -6.67*1*100/abs(r) and observe the closeness of fit of the orange color line (data collected) versus the teal color line (model proposed).
Suggest with reason why you think the model -6.67*1*100/abs(r) is accurate.
Note that the model already has a multiple of x10-11 so there is no need to key it.
7.3.6 Model:
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits


![]()
 This email address is being protected from spambots. You need JavaScript enabled to view it.; Anne Cox; Wolfgang Christian; Francisco Esquembre
This email address is being protected from spambots. You need JavaScript enabled to view it.; Anne Cox; Wolfgang Christian; Francisco Esquembre
end faq
Apps
https://play.google.com/store/apps/details?id=com.ionicframework.gravity05app896563&hl=en