About
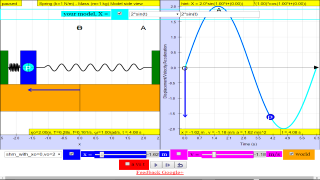
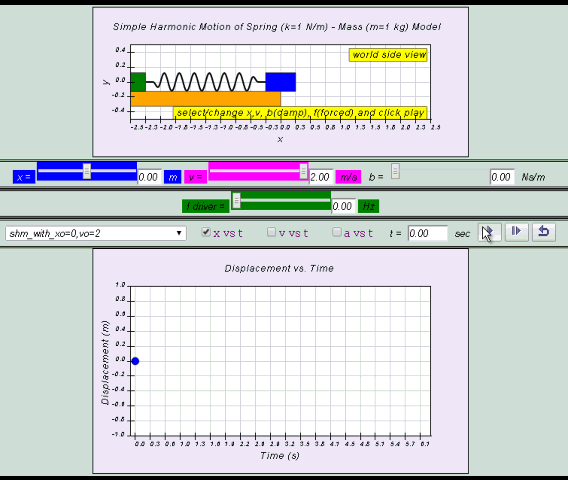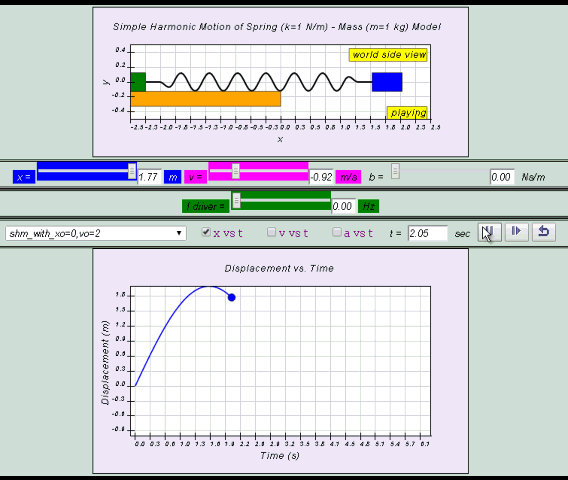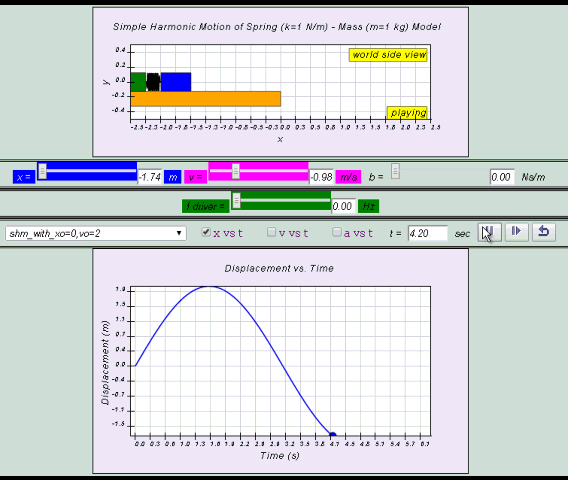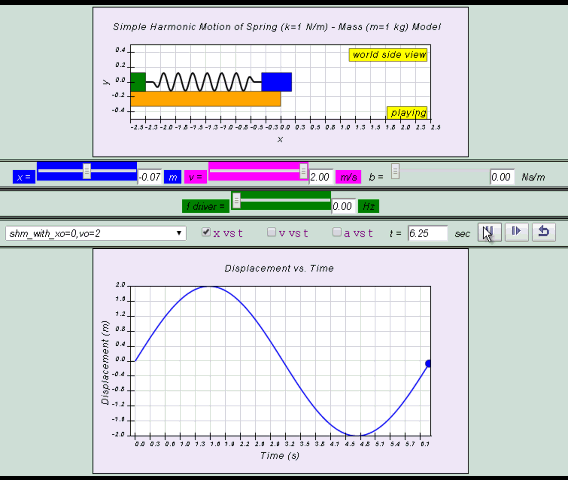
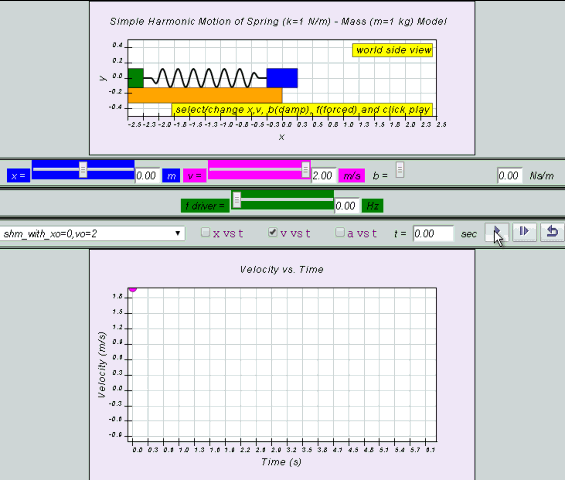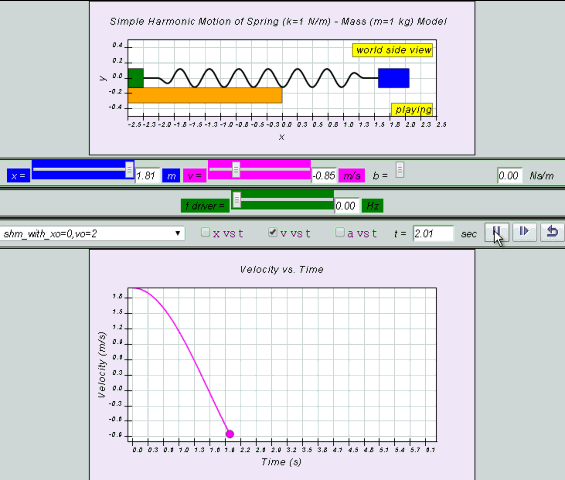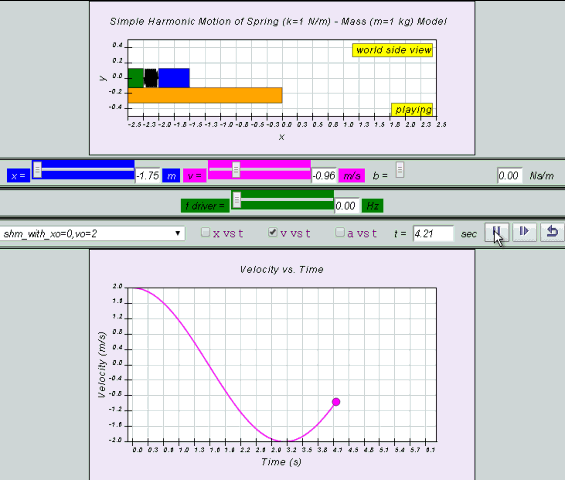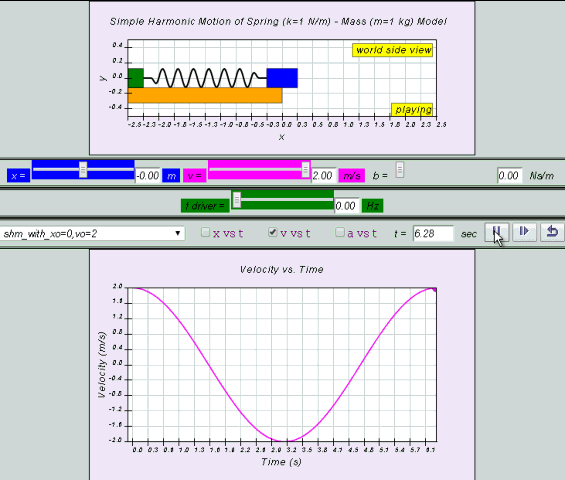
10.2.2 Special Case (starting from x=0) Solution to the defining equation:LO (e)*
x= x0 sin( ωt )
Note:
Equation for v can also be obtained by differentiating x with respect to time t.
v = x0 ω cos (ωt ) = v0 cos (ωt)
Note:
Equation for a can also be obtained by differentiating v with respect to time t.
a = - x0 ω2 sin (ωt ) = - a0 sin (ωt)
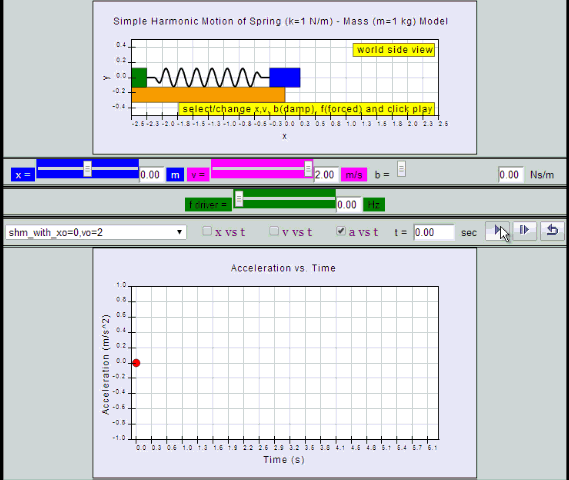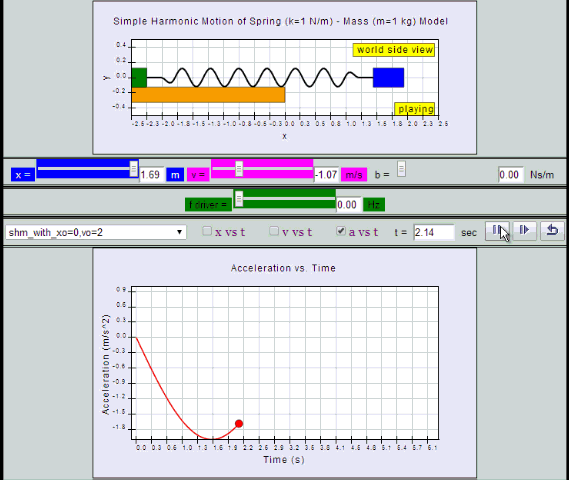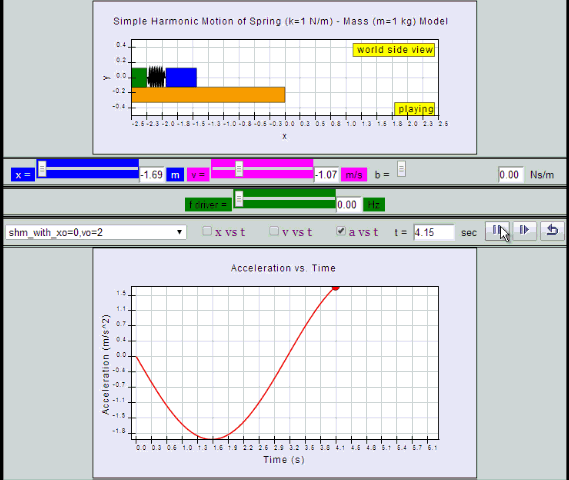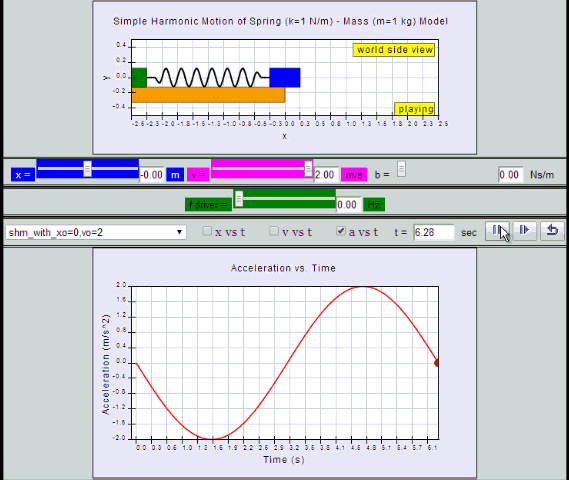
10.2.2.1 Model:
- http://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_SHM08/SHM08_Simulation.xhtml
- http://iwant2study.org/ospsg/index.php/interactive-resources/physics/02-newtonian-mechanics/09-oscillations/71-shm08
by substitution, suggest if the defining equation a = - ω2 x is true or false.
10.2.2.2 Suggest there Special Case (starting from x=x0 ) Solution to the defining equation:LO (e) if given
x= x0 cos( ωt )v = -x0 ω sin (ωt ) = -v0 sin (ωt)
a = -x0 ω2 cos (ωt ) = - a0 cos (ωt)
by substitution, suggest if the defining equation a = - ω2 x is true or false.
10.2.2.3 Summary:
| Quantity | extreme left | centre equilibrium | extreme right |
| x | – x0 | 0 | x0 |
| v | 0 | + x0ω when v >0 or – x0ω when v <0 which are maximum values |
0 |
| a | +x0ω2 | 0 | –x0ω2 |
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits
 This email address is being protected from spambots. You need JavaScript enabled to view it.
This email address is being protected from spambots. You need JavaScript enabled to view it.
end faq
Facebook Social Comments