About
1.2.3 Velocity LO (f)
From x = xo sin ω t
differentiating we get
where v0 = x0 ω is the maximum velocity
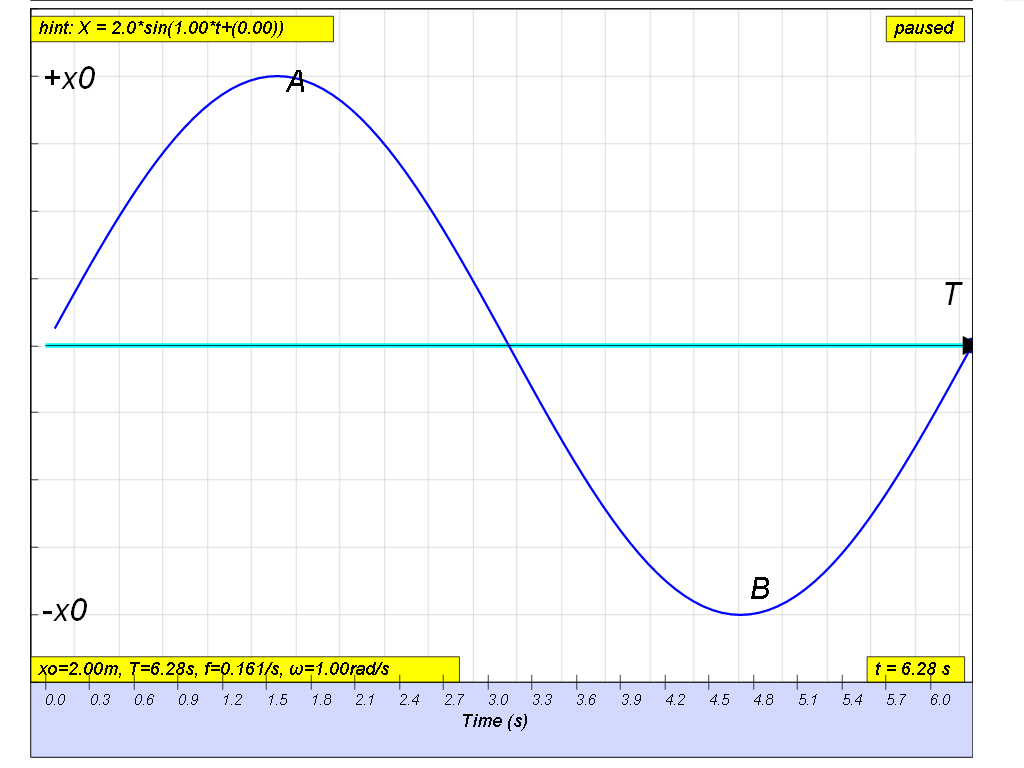
Variation with time of velocity
In terms of x:
From mathematical identity cos2 ωt + sin2 ωt = 1,
rearranging
cos2 ωt = 1 - sin2 ωt
since
v = x0ω cos ωt
where x0 is the maximum displacement
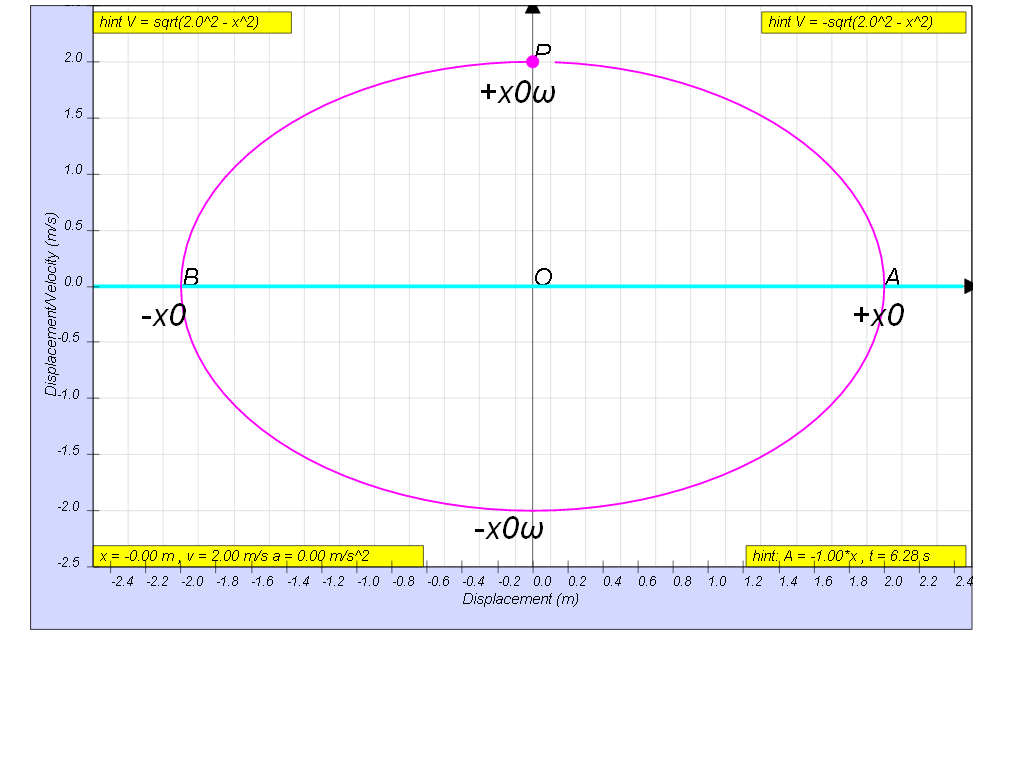
Variation with displacement of velocity
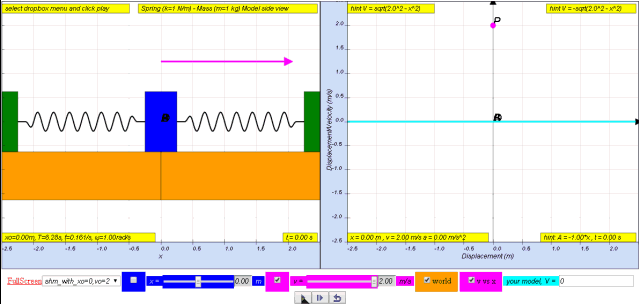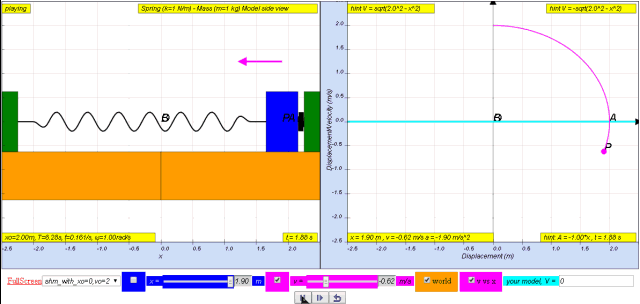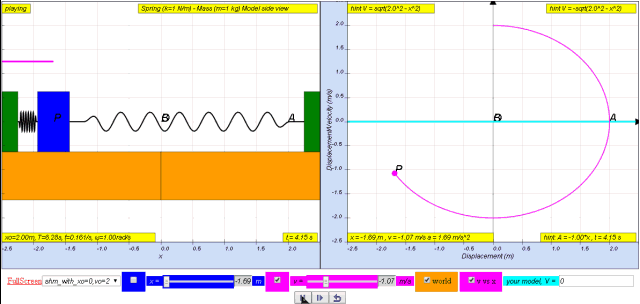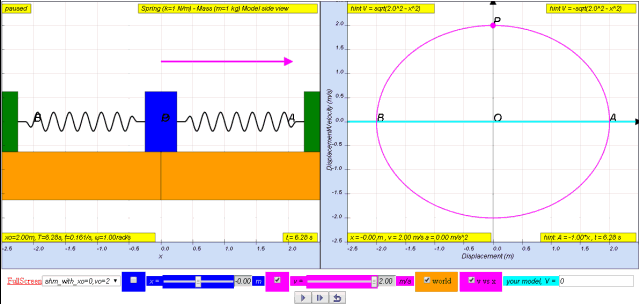
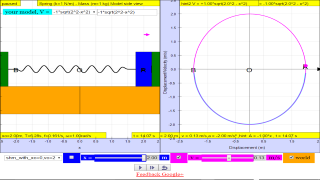
1.2.3.1 Model:
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits
 This email address is being protected from spambots. You need JavaScript enabled to view it.
This email address is being protected from spambots. You need JavaScript enabled to view it.
end faq
Apps
https://play.google.com/store/apps/details?id=com.ionicframework.shm09app611123&hl=en
end faq
Facebook Social Comments