About
1.6 Degrees of damping LO (i)
If no frictional forces act on an oscillator (e.g. mass-spring system,
simple pendulum system, etc.), then it will oscillate indefinitely.
In practice, the amplitude of the oscillations decreases to zero as a
result of friction. This type of motion is called damped harmonic motion.
Often the friction arises from air resistance (external damping) or
internal forces (internal damping).
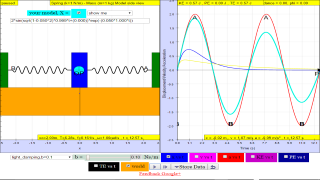
1.6.1 if the motion is x= x0 sin(ωt), the following are the x vs t graphs for 2 periods, as an illustration of the damping.
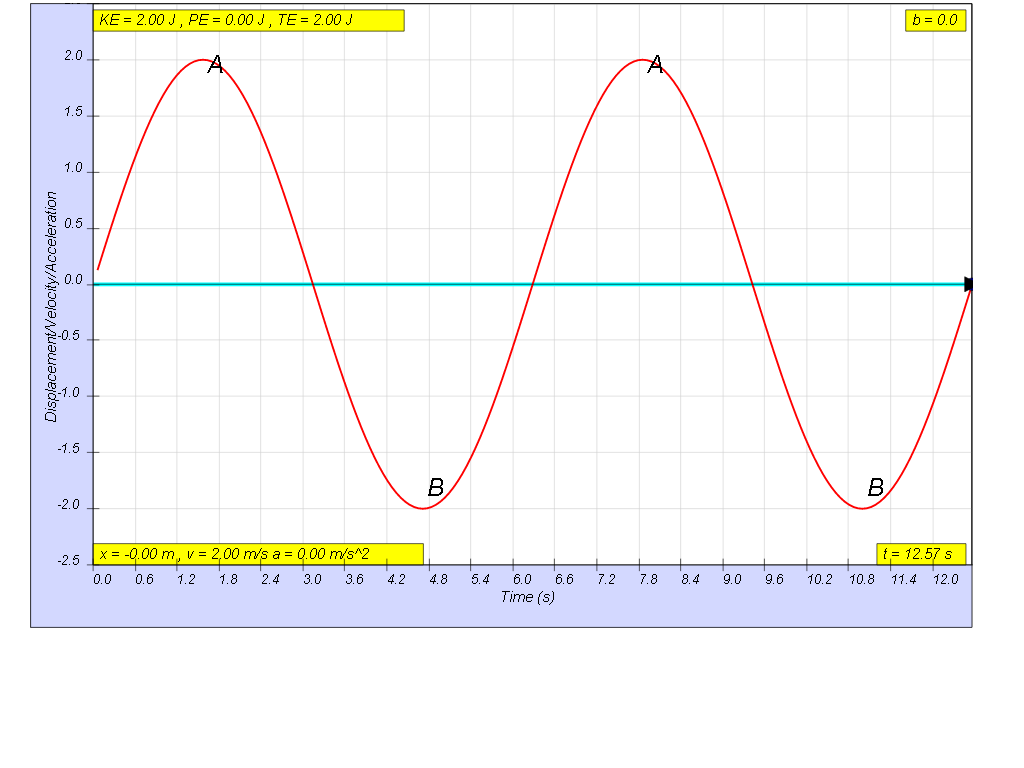
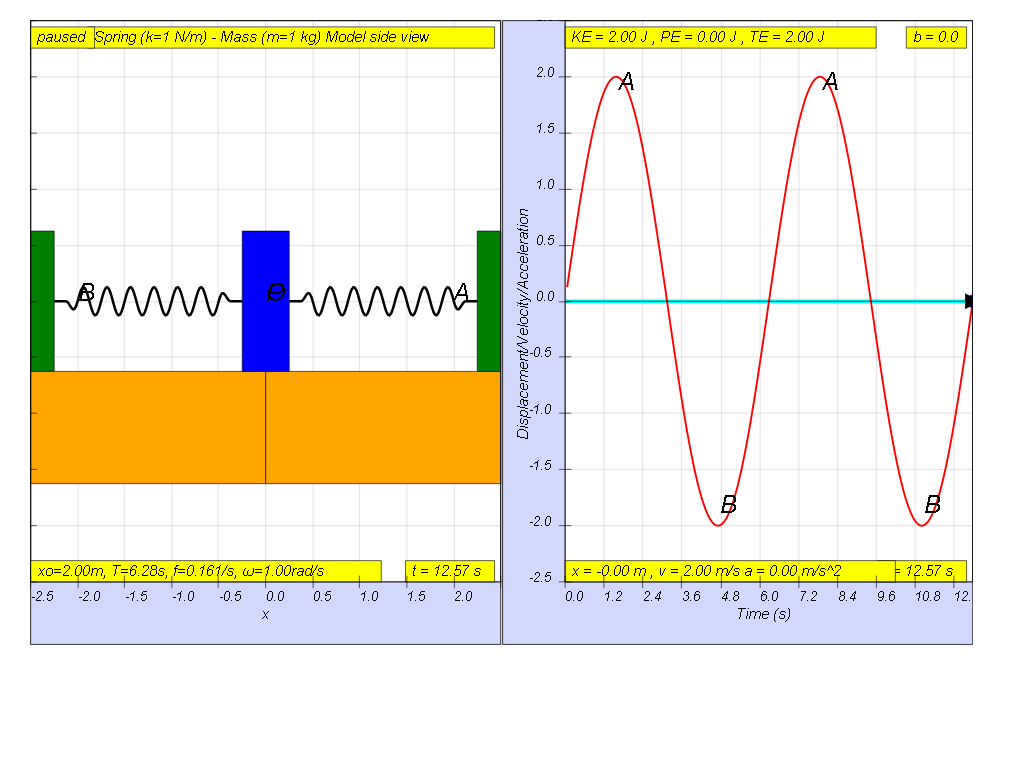
1.6.1.1 No damping
when b=0.0 no damping, system oscillates forever without coming to rest. Amplitude and thus total energy is constant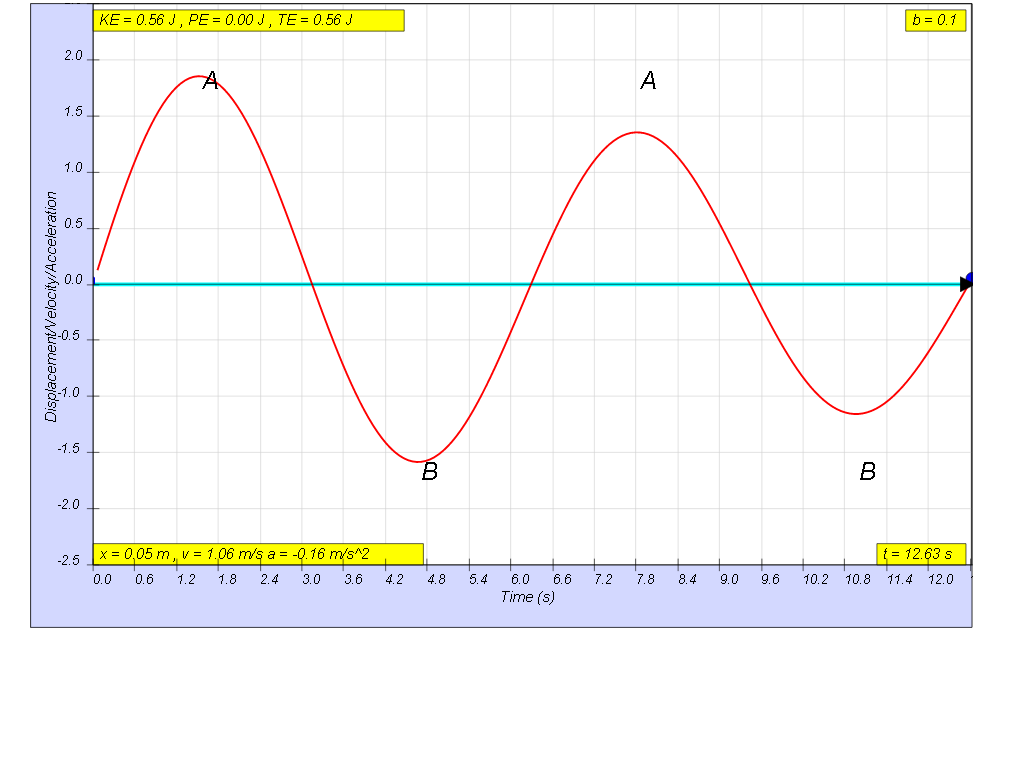
1.6.1.2 Light damping
when b=0.1 very lightly damp, system undergoes several oscillations of decreasing amplitude before coming to rest. Amplitude of oscillation decays exponentially with time.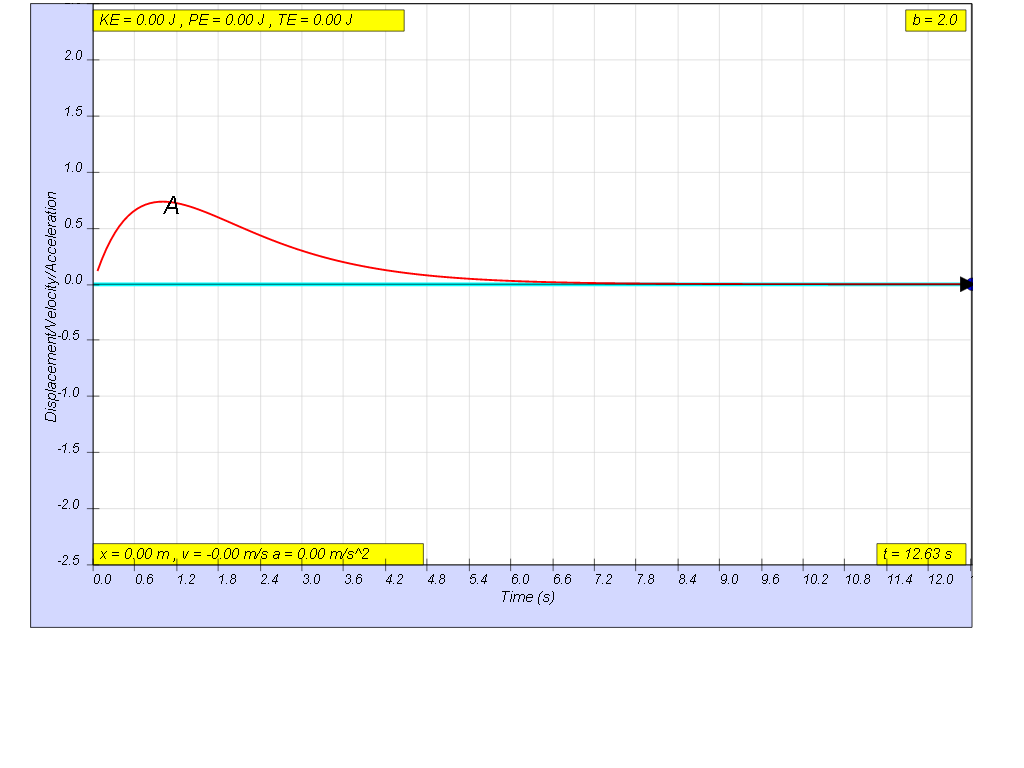
1.6.1.3 Critical damping
when b=2.0, critically damp system returns to equilibrium in the minimum time, without overshooting or oscillating about the equilibrium position amplitude.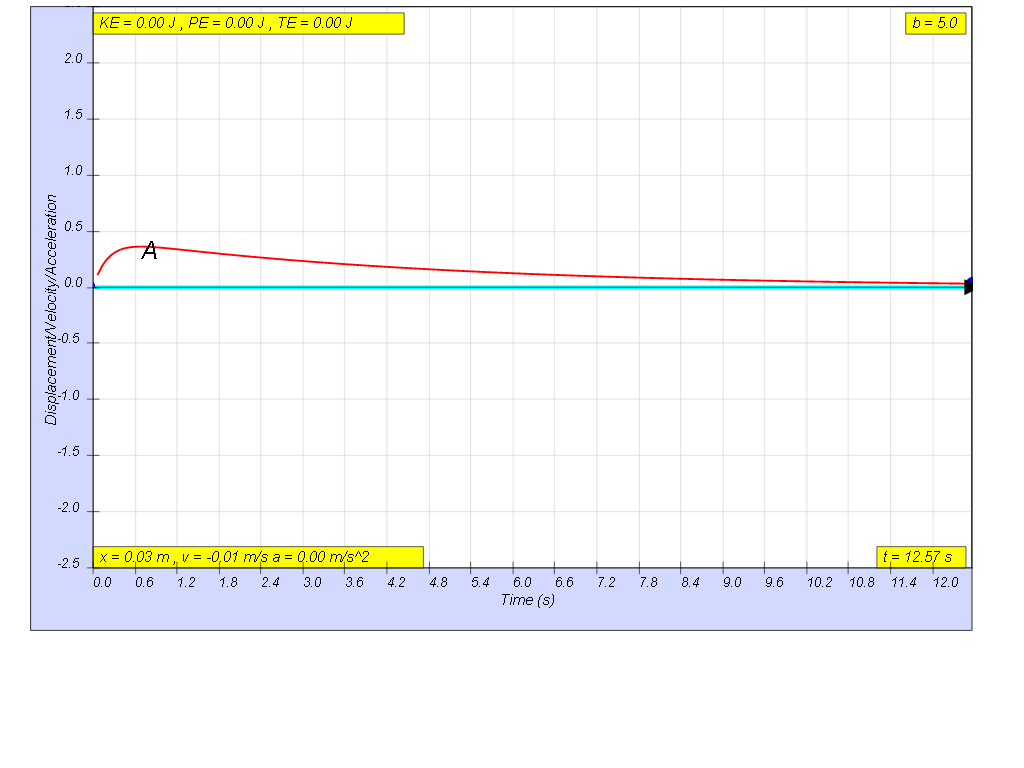
1.6.1.4 Heavy damping
when b=5.0, very heavy damp, system returns to equilibrium very slowly without any oscillation1.6.2 a more typical starting position, is x= x0 cos(ωt), the following are the x vs t graphs for 2 periods, as an illustration of the damping.
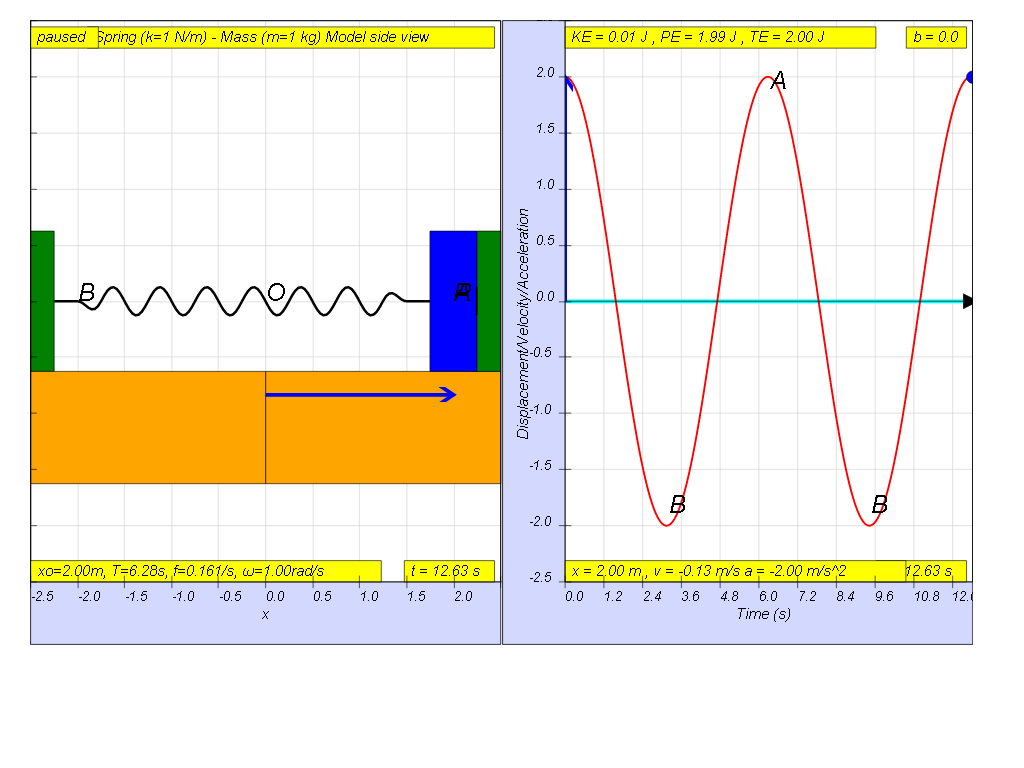
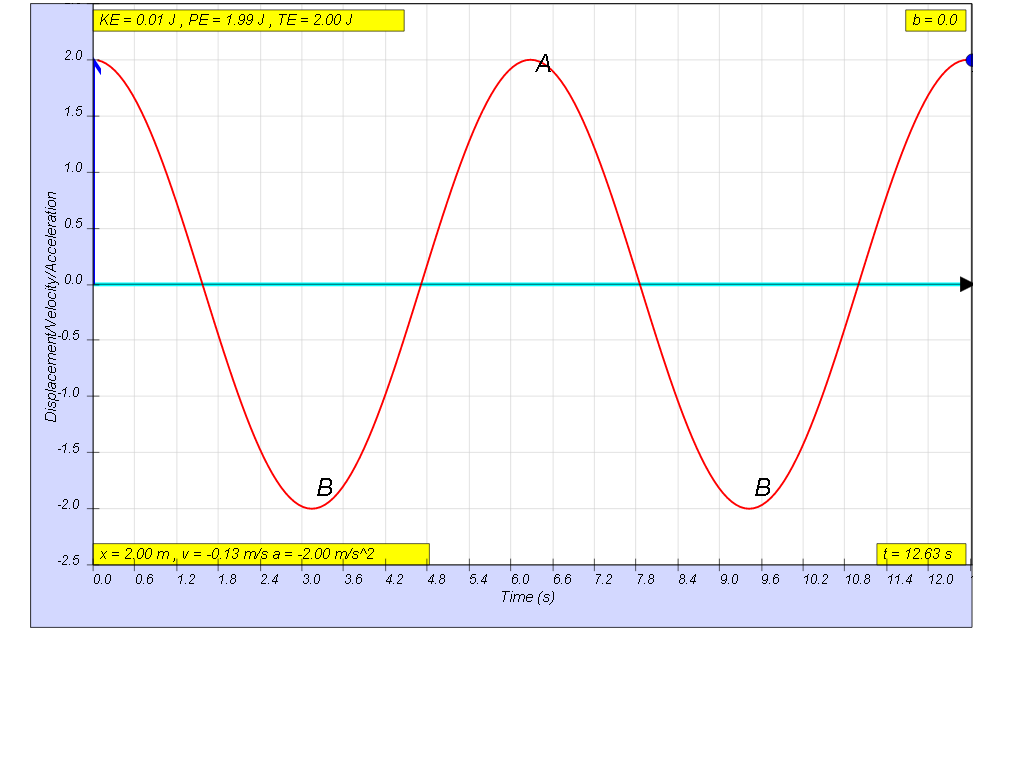
1.6.2.1 No damping
when b=0.0 no damping, system oscillates forever without coming to rest. Amplitude and thus total energy is constant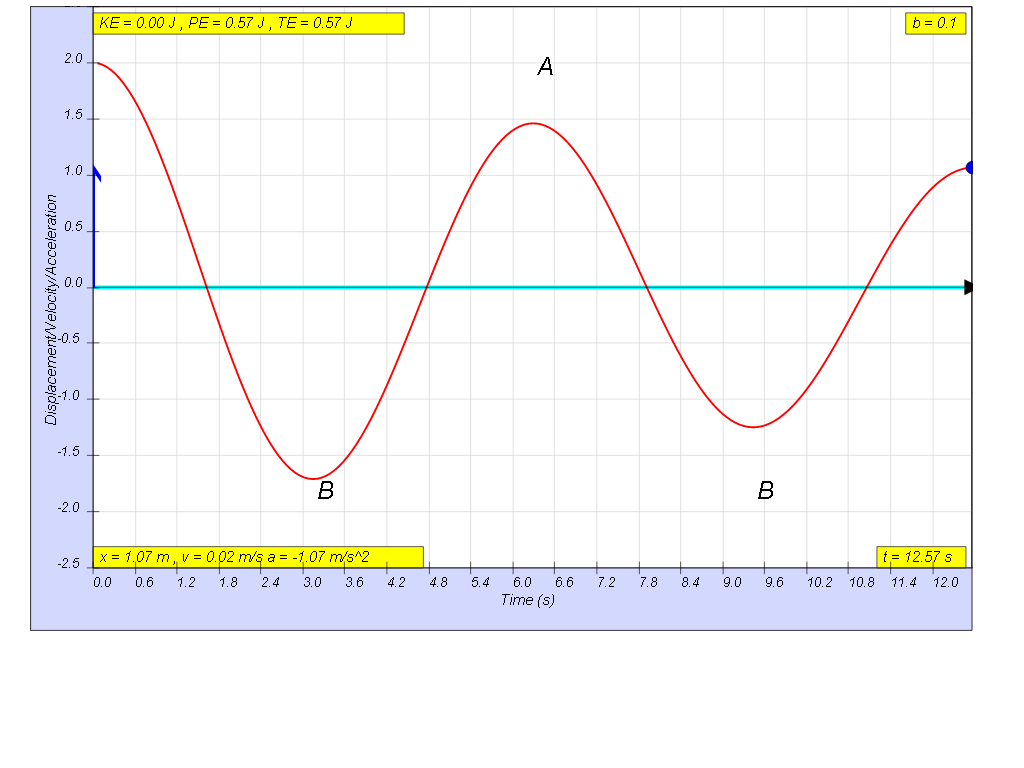
1.6.2.2 Light damping
when b=0.1 very light damping, system undergoes several oscillations of decreasing amplitude before coming to rest. Amplitude of oscillation decays exponentially with time.
1.6.2.3 Critical damping
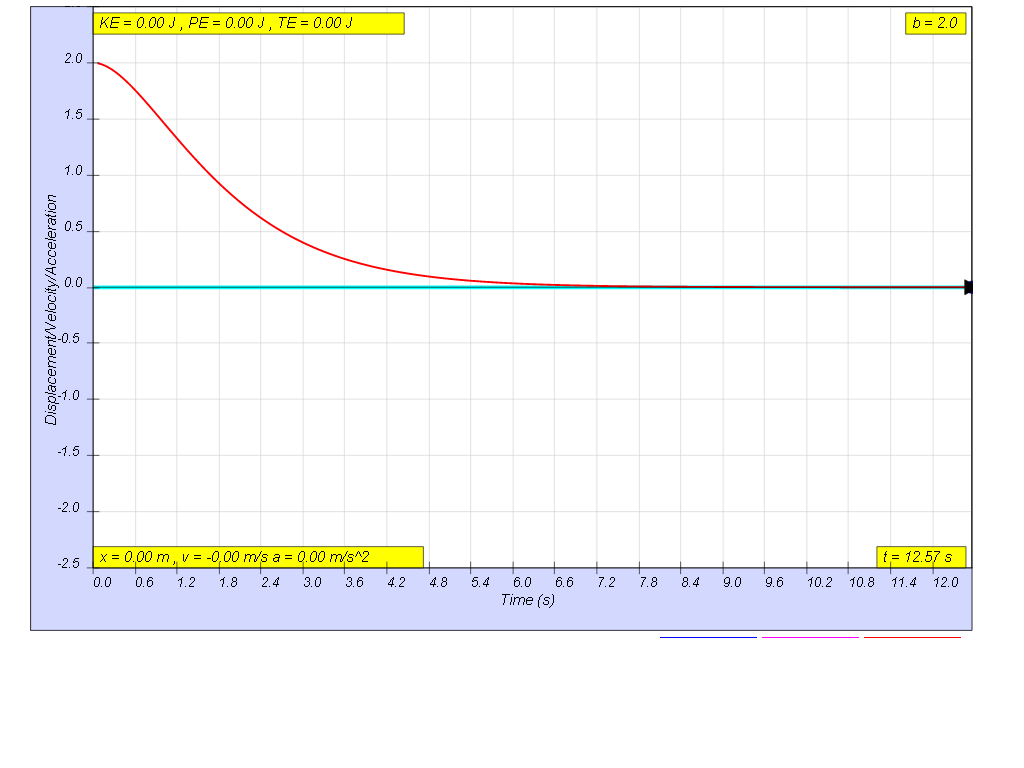
when b=2.0 critically damp, system returns to equilibrium in the minimum time, without overshooting or oscillating about the equilibrium position amplitude.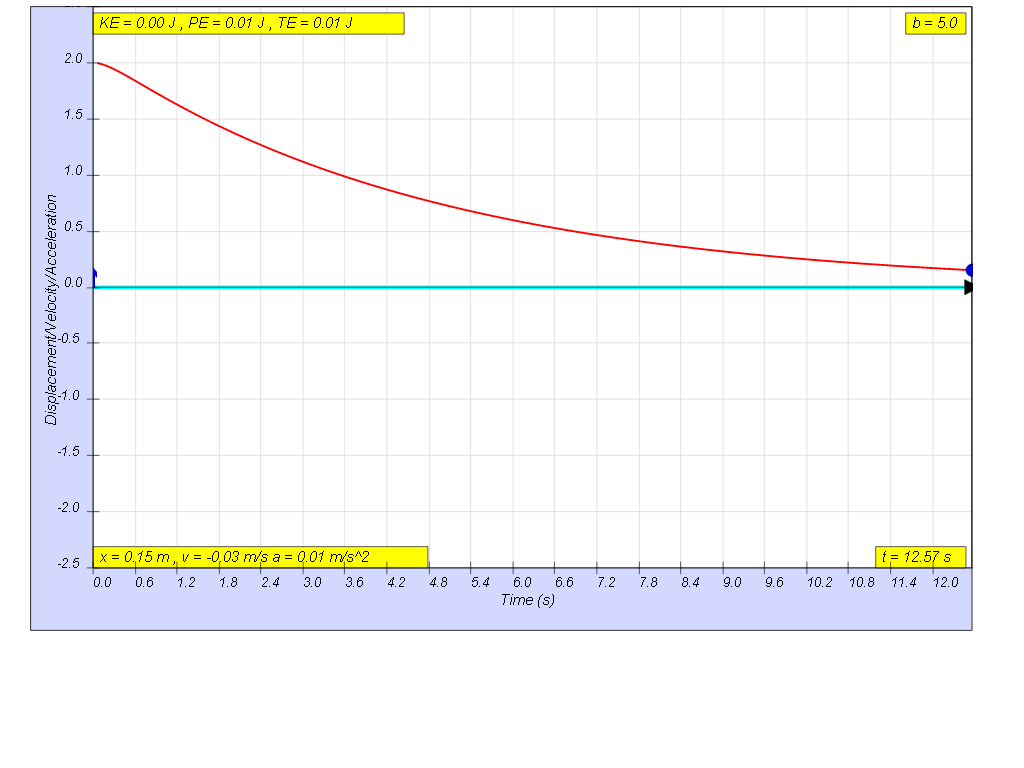
1.6.2.4 Heavy damping
when b=5.0 very heavy damp, system returns to equilibrium very slowly without any oscillation.1.6.3 Model:
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits
 lookang
lookang
end faq
Apps
https://play.google.com/store/apps/details?id=com.ionicframework.shm20app163344&hl=en
end faq
Facebook Social Comments