About
1.1.3.2.3 Understanding Phase Difference through Uniform Circular Motion
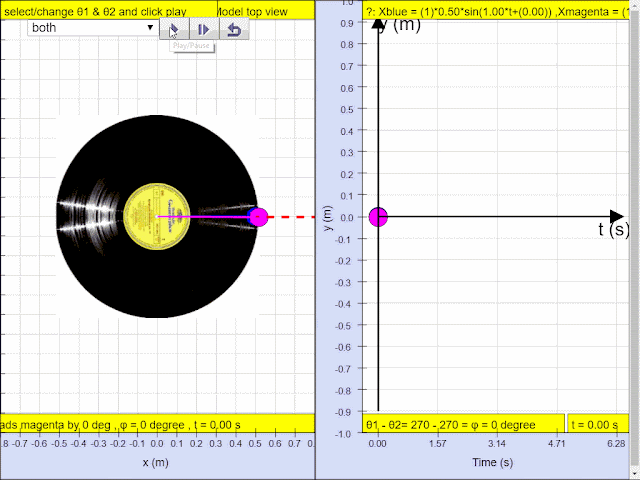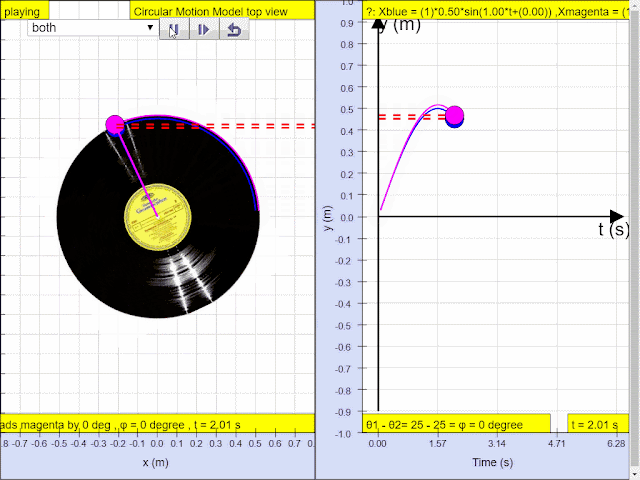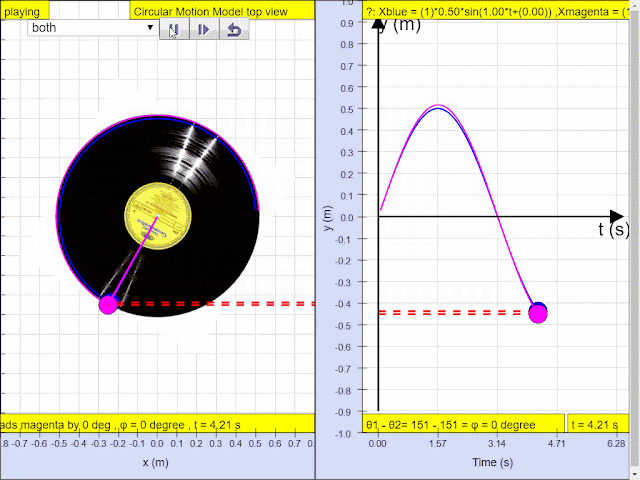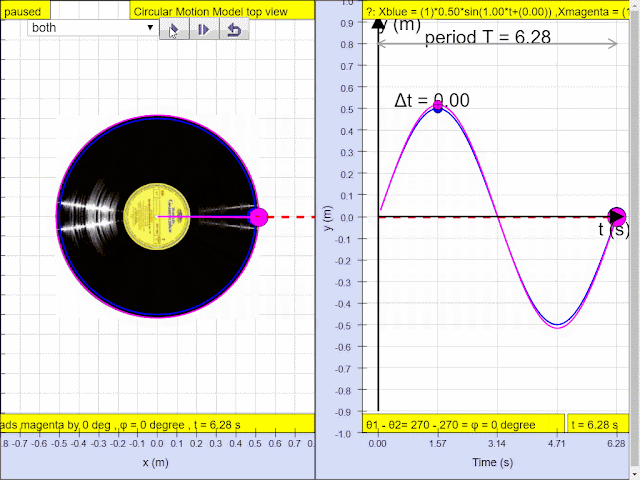
Simple harmonic motion can in some cases be considered to be the one-dimensional projection of uniform
circular motion. If an object moves with angular speed ω around a circle of radius A centered at the origin of the x−y plane, then its motion along each coordinate is simple harmonic motion with amplitude A and angular frequency ω.
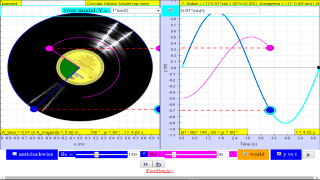
Q1: given that, a circular motion can be described by x = A cos(ω t) and y A sin(ω t) what is the y-component model-equation that can describe the motion of a uniform circular motion?
A1: y = Asin (ωt)
Q2: When the x-component of the circular motion is modelled by x = A cos(ω t) and y A sin(ω t) suggest an model-equation for y.
A2: y = Acos (ωt) for top position or y = - Acos (ωt) for bottom position
Q3: Explain why are the models for both x and y projection of a uniform circular motion, a simple harmonic motion?
A3: both x = A cos(ω t) and y A sin(ω t) each follow the defining relationship for SHM as ordinary differential equations of and respectively.
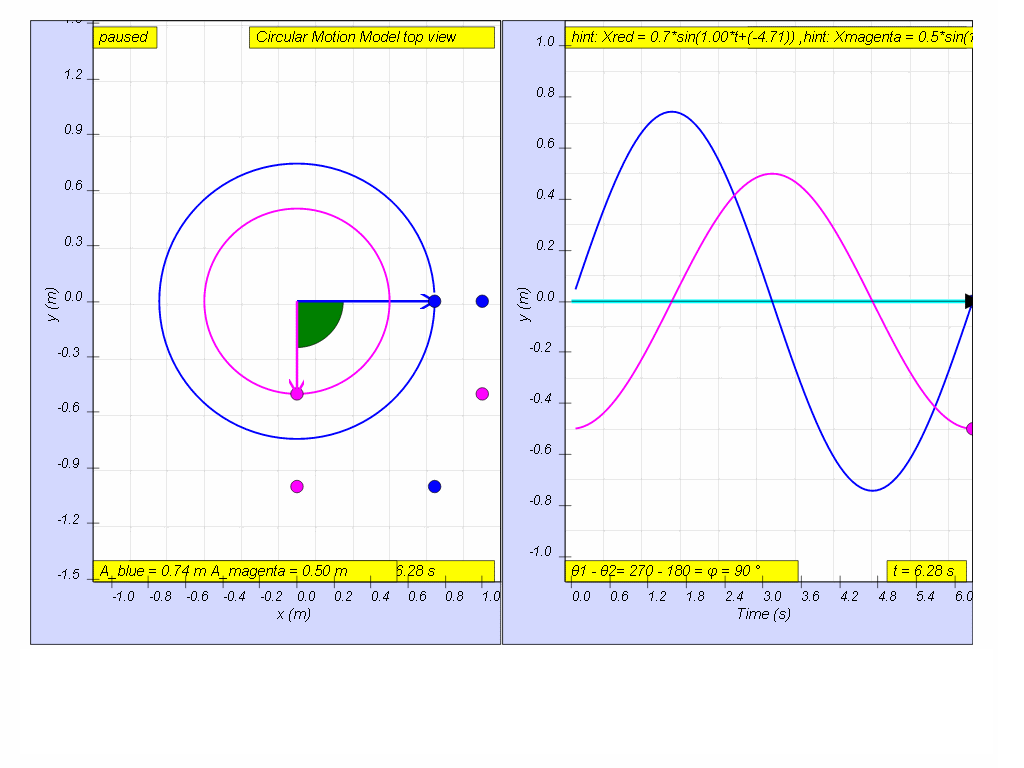
Q4: In, the diagram above, what is the phase difference between blue and magenta color y direction motion?
A4: the phase difference is 90 degrees, or more precisely blue lead red by 90 degrees angle.1.1.3.2.3.1 YouTube:
http://youtu.be/0IaKcqRw_Ts This video shows how a pendulum's oscillations and the shadow of rotating object are related. This could be used to demonstrate that the projection of a circular motion is actually a simple harmonic motion.
1.1.3.2.3.2 Run Model:
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits

 This email address is being protected from spambots. You need JavaScript enabled to view it.; Fu-Kwun Hwang
This email address is being protected from spambots. You need JavaScript enabled to view it.; Fu-Kwun Hwang
end faq
What is in Phase?
 |
Video
Version:
Other Resources
[text]