https://iwant2study.org/moodle402/mod/laejss/view.php?id=41
About
Topics
Progressive wavesTransverse and
Determination of frequency and wavelength
Stationary waves
Description
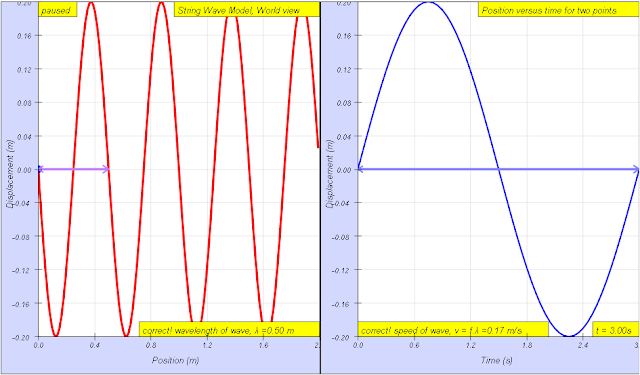
In this Wave representations simulation, you have two representations of wave motion to work with. The left one shows a movie of the wave traveling along a string - you can think of this representation as a sequence of photographs. The second right representation is a plot of the displacement as a function of time for two points on the string (you can select which two points to use). Using only these two representations, you can determine the values of many different parameters that describe the wave by changing the slider values or input fields. Hints have also been designed in for ease of visualizing the meaning of these parameters.
Play with the Wave Representations Model. Test what you've learned by exploring the amplitudes, wavelengths, periods, angular frequency, frequencies, wave velocities, maximum transverse velocity (linking to simple harmonic motion) and phase difference.
Sample Learning Goals
(a) show an understanding and use the terms displacement, amplitude, phase difference, period,frequency, wavelength and speed
(b) deduce, from the definitions of speed, frequency and wavelength, the equation v = fλ
(c) recall and use the equation v = fλ
(f) analyse and interpret graphical representations of transverse
(c) SHM: understand and use the terms amplitude, period, frequency, angular frequency and phase difference and express the period in terms of both frequency and angular frequency
Activities
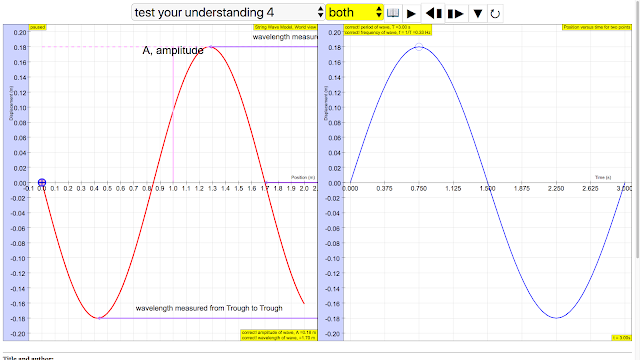
Reset the simulation to get a new random wave you are happy with.Amplitude, A and wavelength, λ can be determined using the left graph of displacement versus position.
Then, play the simulation until you have a nice position versus time graph. Period, T and angular frequency, ω and frequency, f and phase difference between x1 and x2, φ using the relationship φ/(2π) = t/T, where t is the time difference between x1 and x2, can be determined using the right graph of displacement of x1 and x2 versus time.
Using both graphs, it is possible to determine wave velocity v = f λ, maximum transverse speed of a single point on the string, vmax= A ω. You can check your answers as many times as you want. The amplitude. The wavelength. The period. The angular frequency. The wave speed. The maximum transverse speed of a single point on the string.
Version:
- http://weelookang.blogspot.sg/2015/08/ejss-wave-representation-model.html
- http://weelookang.blogspot.sg/2011/04/ejs-open-source-wave-representations.html
- http://iwant2study.org/lookangejss/04waves_12generalwaves/ejs/ejs_model_Wave_representations_v5.jar
-
http://weelookang.blogspot.sg/2015/08/ejss-wave-representation-model.html
Wave representations
In this simulation, you have two representations of wave motion to work with. One shows a movie of the wave traveling along a string - you can think of this representation as a sequence of photographs. The second representation is a plot of the displacement as a function of time for two points on the string (you can select which two points to use). Using only these two representations, you can determine the values of many different parameters that describe the wave.
For more info : http://weelookang.blogspot.sg/2011/04/ejs-open-source-wave-representations.html
Activities
Keep pressing the "Get a new wave" button until you have a wave you are happy with. Then, play the simulation until you have a nice position versus time graph. Then, pause the simulation so that you have a photograph of the string as well as your position vs. time graph to work with. For each parameter below, figure out which of the two representations you need to determine the value of the parameter, and then find the value. You can check your answers as many times as you want.
- The amplitude.
- The wavelength.
- The period.
- The angular frequency.
- The wave speed.
- The maximum transverse speed of a single point on the string.
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits


Andrew Duffy; lookang; tina
end faq
Apps
Description
Introduction
Wave is an oscillation accompanied by a transfer of energy that travels through medium (space or mass)
Waves consist, instead, of oscillations or vibrations (of a physical quantity), around almost fixed locations
This simulation is on transverse wave where disturbance creates oscillations that are perpendicular to the propagation of energy transfer.
The equation for wave is A sin ( wt +kx + ϕ)
where
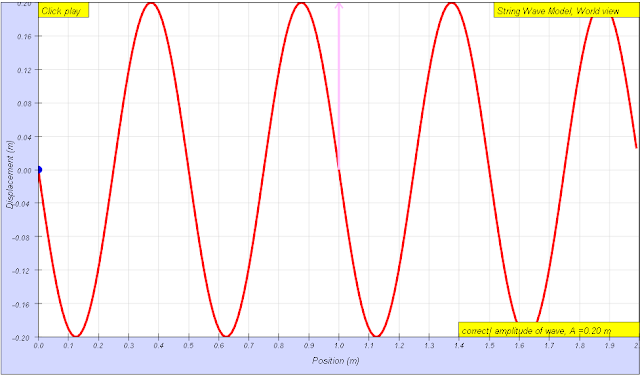
A is the maximum amplitude of the wave, maximum distance from the highest point of the disturbance in the medium (the crest) to the equilibrium point during one wave cycle.
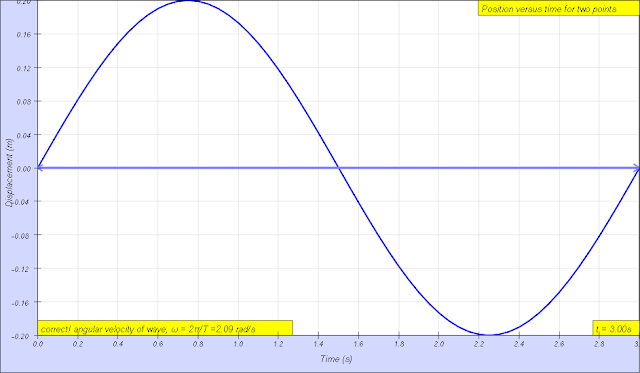
w is is the angular frequency
t is time
k is is the wavenumber
x is the position
ϕ is the is the phase constant
concepts illustrated in the simulations include
T is the time for one complete cycle of an oscillation of a wave
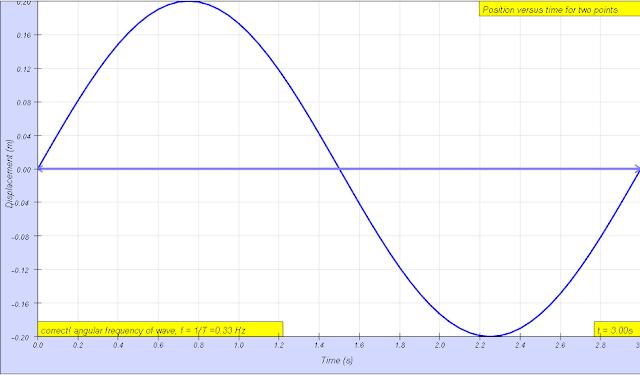
f is the number of periods per unit time (per second) and is related by T = 1/f
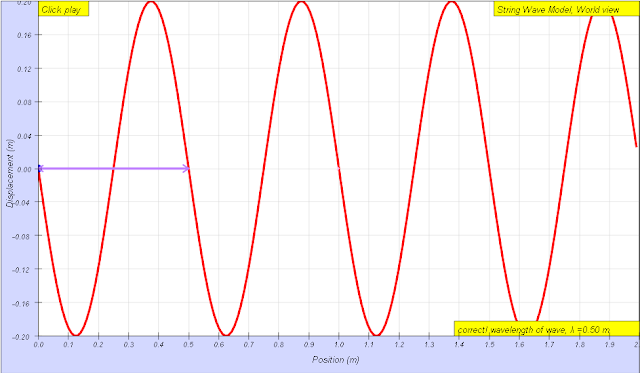
λ is the wavelength
v is the velocity of the wave travelling and is related by v= f λ
vtmax is the maximum transverse velocity of the wave particle that occurs at the displacement d =0.
Examples
EJSS wave representation model
Equation used to model the wave is \( y = A sin ( \omega t - k x ) \)
Amplitude A
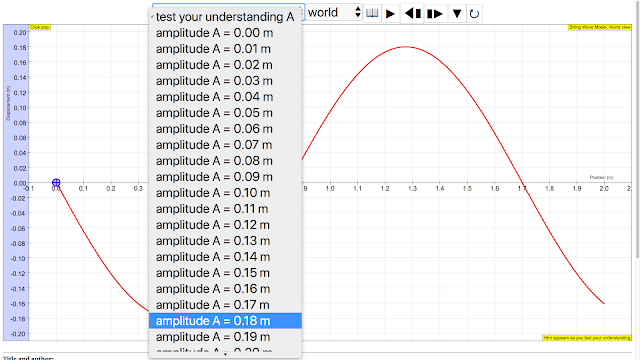 |
| amplitude of wave = 0.18 m, maximum displacement from equilibrium position http://iwant2study.org/ospsg/index.php/112 Direct Link |
|
amplitude of wave = 0.20 m, maximum displacement from equilibrium position author: Andrew Duffy, lookang, tina author EJS: Francisco Esquembre |
wavelength λ
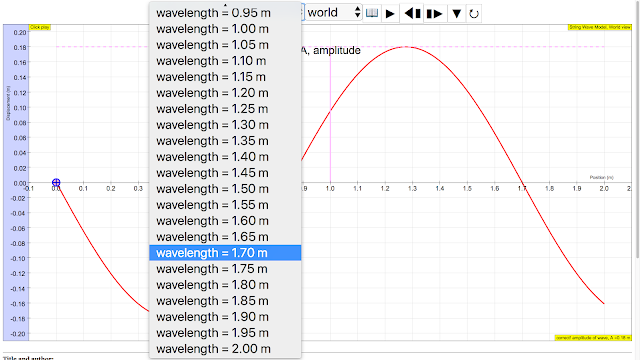 |
|
wavelength of wave = 1.70 m The wavelength λ wavelength is the distance between two sequential crests or troughs (or other equivalent points) |
|
wavelength of wave = 0.50 m The wavelength λ wavelength is the distance between two sequential crests or troughs (or other equivalent points) author: Andrew Duffy, lookang, tina author EJS: Francisco Esquembre |
Period T
 |
| period of wave = 3.00 s, The period T is the time for one complete cycle of an oscillation of a wave http://iwant2study.org/ospsg/index.php/112 Direct Link |
|
period of wave = 3.00 s, The period T is the time for one complete cycle of an oscillation of a wave author: Andrew Duffy, lookang, tina author EJS: Francisco Esquembre |
angular frequency f
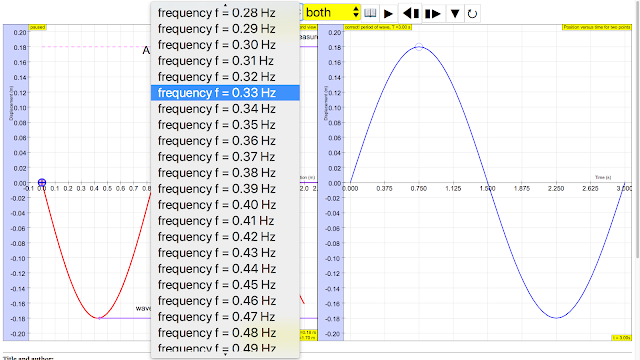
 |
| The frequency f = 1/T is the number of periods per unit time (per second) and is typically measured in hertz http://iwant2study.org/ospsg/index.php/112 Direct Link |
|
The frequency f = 1/T is the number of periods per unit time (per second) and is typically measured in hertz author: Andrew Duffy, lookang, tina author EJS: Francisco Esquembre |
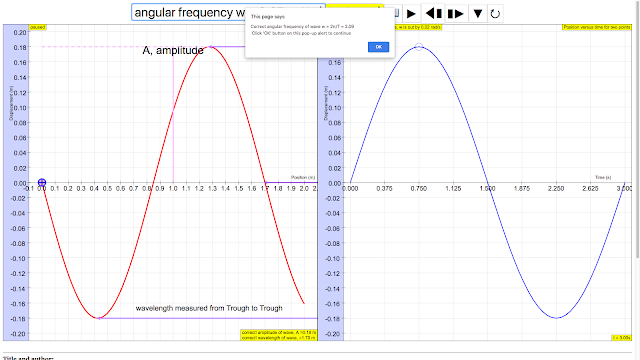
angular velocity of wave ω
 |
| angular frequencyω = 2.09 s, The angular frequencyω represents the frequency in radians per second. http://iwant2study.org/ospsg/index.php/112 Direct Link |
|
angular frequencyω = 2.09 s, The angular frequencyω represents the frequency in radians per second. author: Andrew Duffy, lookang, tina author EJS: Francisco Esquembre |
phase difference ϕ
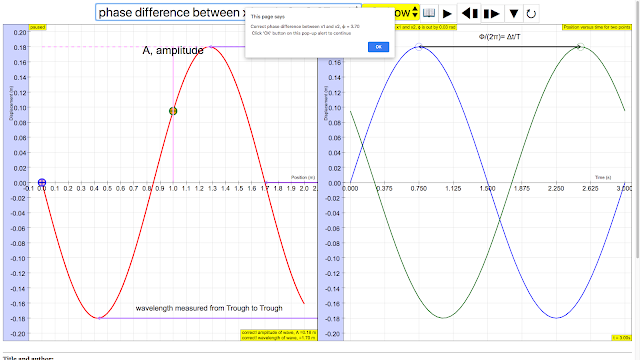 |
|
the phase of a vibration (that is, its position within the vibration cycle) ϕ measured in radians taking ratio "ϕ/(2π)= Δt/T", ϕ = 2π(2.5-0.75)/3 =3.7 rad approximately |
wave speed v
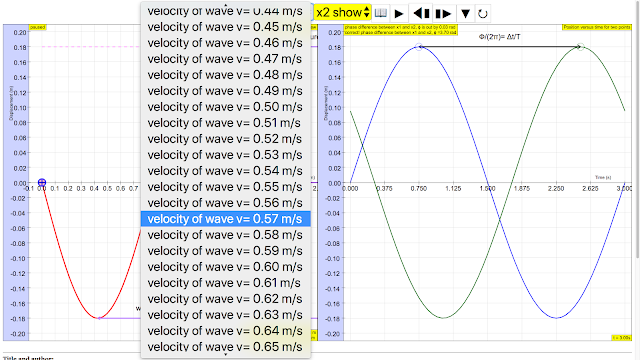 |
| sinusoidal waveform traveling at constant speed v is given by v = f λ http://iwant2study.org/ospsg/index.php/112 Direct Link |
|
sinusoidal waveform traveling at constant speed v is given by v = f λ author: Andrew Duffy, lookang, tina author EJS: Francisco Esquembre |
maximum transverse speed vmax
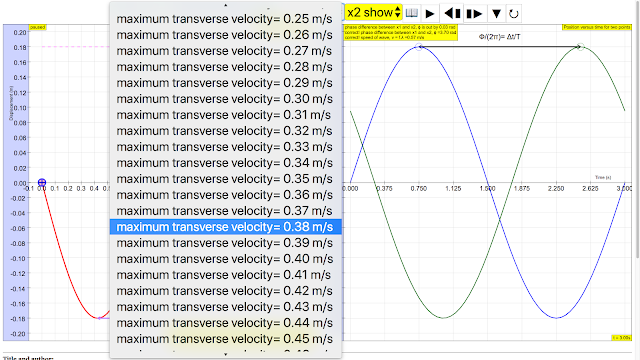 |
| The maximum transverse velocity is vmax = Aω and it occurs when the particle on the wave travels passes through the equilibrium position http://iwant2study.org/ospsg/index.php/112 Direct Link |
|
The maximum transverse velocity is vmax = Aω and it occurs when the particle on the wave travels passes through the equilibrium position author: Andrew Duffy, lookang, tina author EJS: Francisco Esquembre |
reference:
http://weelookang.blogspot.sg/2011/04/ejs-open-source-wave-representations.html
Video
Versions
- http://weelookang.blogspot.sg/2015/08/ejss-wave-representation-model.html Blog post of JavaScript version of Wave Representations by Andrew Duffy and Loo Kang Wee
- http://weelookang.blogspot.sg/2011/04/ejs-open-source-wave-representations.html Blog post of Java version of Wave Representations by Andrew Duffy and Loo Kang Wee
- http://iwant2study.org/lookangejss/04waves_12generalwaves/ejs/ejs_model_Wave_representations_v5.jar Java version of Wave Representations by Andrew Duffy and Loo Kang Wee
Other Resources
- http://physics.bu.edu/~duffy/HTML5/wave_movie_and_graph.htmlby Andrew Duffy
- http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=2405.0 One dimensional moving wave y(x,t)=A sin(k*x-w*t) by Fu-Kwun Hwang

.png
)