About

Subject Area	Waves & Optics
Levels	First Year and Beyond the First Year
Available Implementation	Python
Learning Objectives	Students who complete this set of exercises will be able to predict and visually represent the irradiance distribution at a screen generated by a point light source and an aperture (Exercise 1); predict and visually represent the irradiance distribution at a screen generated by multiple point light sources and an aperture (Exercise 2); predict and visually represent the irradiance distribution at a screen generated by multiple point light sources and a complex aperture (Exercise 3); predict and visually represent the irradiance distribution at a screen generated by a two-dimensional array of point light sources and an aperture (Exercise 4);, and predict and visually represent the irradiance distribution at a screen generated by a two-dimensional array of point light sources and an opaque barrier (Exercise 5).
Time to Complete	120 min

EXERCISE 1: IRRADIANCE AT A SCREEN DUE TO A POINT SOURCE

We imagine that a point source of light at Ps=(xs,ys,zs)$P_s=(x_s,y_s,z_s)$ illuminates an aperture in an opaque barrier located at z=0$z=0$ as shown below.

The irradiance of the light appearing at point P=(x,y,z)$P=(x,y,z)$ on the viewing screen located at z=zsc$z=z_{sc}$ is then given by

where A$A$ is a constant, r$r$ is the distance from PS$P_S$ (the source) to P$P$ (the screen point), and T(x,y)$T(x,y)$ is a function we call the ‘transparency function’. If the line from the source at Ps$P_s$ to the screen point P$P$ passes through the aperture, then T(x,y)=1$T(x,y)=1$; otherwise, T(x,y)=0$T(x,y)=0$. In the case where the aperture is a rectangle of width w$w$ in the x$x$-direction and height h$h$ in the y$y$-direction, show that the value of the transparency function is given byAlt Figure

Compute the irradiance on an array of uniformly spaced screen points on the viewing screen for an aperture with w=4.0$w=4.0$ cm and h=3.0$h=3.0$ cm in the following cases:

xS$x_S$ [cm]	yS$y_S$ [cm]	zS$z_S$ [cm]	zsc$z_{sc}$ [cm]
0.0	0.0	-20.0	40.0
5.0	0.0	-20.0	40.0
0.0	5.0	-20.0	40.0
0.0	0.0	-10.0	40.0
0.0	0.0	-40.0	40.0
0.0	0.0	-20.0	60.0
0.0	0.0	-20.0	20.0

Does the computed light pattern change as you expect when you change the source and screen locations? Are the edges of the light pattern sharp or fuzzy? (How do you define “sharp” and “fuzzy”?) Why?

#

# Shadows_Exercise_1.py

#

# A point source is located a specified distance from

# a rectangular aperture that is centered on the origin.

# A screen is located a specified distance from

# the aperture.

#

# This file will generate a filled contour plot of

# the irradiance of the light reaching the screen

# versus lateral coordinates (x,y)

#

# Written by:

#

# Ernest R. Behringer

# Department of Physics and Astronomy

# Eastern Michigan University

# Ypsilanti, MI 48197

# (734) 487-8799

# This email address is being protected from spambots. You need JavaScript enabled to view it.

#

# 20160112-13 original code by ERB

# 20160609 clean up by ERB

#

# import the commands needed to make the plot

from pylab import xlabel,ylabel,show,contourf,axis,colorbar,figure,title,xlim,ylim

from matplotlib import cm

# import the command needed to make a 1D array

from numpy import meshgrid,absolute,where,zeros,linspace

# inputs

zs = -20.0 # distance between the source and aperture [cm]

zsc = 40.0 # distance between the screen and aperture [cm]

rso = [5.0,0.0] # (x,y) location of the source [cm,cm]

ap_width = 4.0 # aperture width [cm]

ap_height = 3.0 # aperture height [cm]

screen_width = 60.0 # screen width [cm]

screen_height = 60.0 # wcreen height [cm]

nw = 240 # Number of screen width intervals

nh = 240 # Number of screen height intervals

# initialize needed arrays to zero

screen_x = zeros((nw+1,nh+1)) # x coordinates of screen points

screen_y = zeros((nw+1,nh+1)) # y coordinates of screen points

rsq = zeros((nw+1,nh+1)) # source-to-screen point distance, squared

x0 = zeros((nw+1,nh+1)) # x coordinates of ray intercepts at aperture plane

y0 = zeros((nw+1,nh+1)) # y coordinates of ray intercepts at aperture plane

# initialize values

screen_xx = linspace(-0.5*screen_width,0.5*screen_width,nw+1)

screen_yy = linspace(-0.5*screen_height,0.5*screen_height,nh+1)

# create the meshgrid on which to evaluate the irradiance

screen_xx, screen_yy = meshgrid(screen_xx,screen_yy)

# Calculate grid increments

deltaw = screen_width/nw # grid increment, width [cm]

deltah = screen_height/nh # grid increment, height [cm]

# Define the array of screen x and screen y values

for i in range (0,nw+1):

for j in range (0,nh+1):

screen_x[i,j] = -0.5*screen_width + deltaw*i

screen_y[i,j] = -0.5*screen_height + deltah*j

# Calculate the intensity at each screen point

for i in range (0,nw+1):

for j in range (0,nh+1):

# First calculate the square of the distance from source to screen

rsq = (screen_x[i,j]-rso[0])**2 + (screen_y[i,j]-rso[1])**2 + (zsc - zs)**2

# Calculate x and y coordinates at the aperture

x0[i,j] = rso[0] + abs(zs)*(screen_x[i,j] - rso[0])/(zsc - zs)

y0[i,j] = rso[1] + abs(zs)*(screen_y[i,j] - rso[1])/(zsc - zs)

# Check if the coordinates fall within the aperture

maskx = where(absolute(x0) < 0.5*ap_width,1.0,0.0)

masky = where(absolute(y0) < 0.5*ap_height,1.0,0.0)

# Calculate the intensity

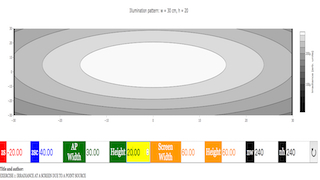
irradiance = maskx*masky/rsq

# make a filled contour plot of the period vs overlap and length ratios

figure()

contourf(screen_yy,screen_xx,irradiance,100,cmap=cm.bone)

axis('equal')

xlim(-0.5*screen_width,0.5*screen_width)

ylim(-0.5*screen_height,0.5*screen_height)

xlabel("\(x\) [cm]",size = 16)

ylabel("\(y\) [cm]",size = 16)

title('Illumination pattern: \(w = \)%s cm, \(h = \)%s'%(ap_width,ap_height),size = 16)

colorbar().set_label(label='Irradiance [arb. units]',size=16)

show()

 

Translations

Code	Language		Translator	Run

Software Requirements

	Android	iOS	Windows	MacOS
with best with	Chrome	Chrome	Chrome	Chrome
support full-screen?	Yes. Chrome/Opera No. Firefox/ Samsung Internet	Not yet	Yes	Yes
cannot work on	some mobile browser that don't understand JavaScript such as.....		cannot work on Internet Explorer 9 and below

 

Credits

Fremont Teng; Loo Kang Wee; based on codes by E. Behringer

end faq