About
The Mandelbrot set
The Mandelbrot set consists of points, c, in the complex plane that obey the following rule
- Start with the complex number z = a + ib where a and b are real numbers.
- Generate a new complex number, z', by multiplying z by itself and adding the result to c. z' = z2 + c.
- Repeat steps 1 and 2. If the complex number z goes toward infinity, then the starting point, c, is not a member of the Mandelbrot set. All numbers that remain bounded are members of the set.
Mandelbrot set
The members of the Mandelbrot set follow the rule
zn+1= zn2+ c ; z0 = 0
c is a complex number, as is z
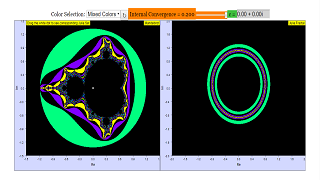
We look for points c in the complex plane, for which the sequence does not diverge. They form the Mandelbrot set. In the simulation they are colored red, lying within a range with fractal boundary, the famous "apple man". Diverging points are colored green to blue, with the color shading indicating the speed of divergence.
Drawing a rectangle with the mouse defines a smaller range of calculation with correspondingly increasing resolution. Reset leads back to the initial condition.
The series has the members 0, c, c2+ c, c4 + 2c3 + c2 + c,...
The fractal structure is caused by the nonlinearity of the sequence rule. It is observed for other nonlinear sequences as well, with different structure of the fractal.
Julia set
The Julia set corresponding to the Mandelbrot set is generated with the same rule : zn+1=zn2+c. Yet with the Julia set c is constant, and we calculate for which point z of the complex plane the sequence converges to a finite non zero value. Each point c of the complex plane has its own Julia set. In the chart with the Mandelbrot set you see a white point that defines c. It can be drawn with the mouse. The right chart displays the corresponding Julia set. Again a calculation range with higher resolution can be defined by drawing a rectangle with the mouse. Reset at the Julia chart leads back to the Julia range for the given magnification in the Mandelbrot chart. Reset at the Mandelbrot chart leads back to the Julia set with c = 0 at the original size of the Mandelbrot set. The Julia set are points at the fractal border. The degree of divergence or convergence to zero is indicated by color shading. Its gradation can be changed by a slider, which produces interesting color schemes. The connection between a basic fractal and its Julia set are similar with different set rules.Julia set
When opening the simulation or at Reset at the chart of the Julia set you see the unit circle surrounded inside and outside by circular blue shaded areas.
The green rim of the unit circle is the Julia set of the white point c = (0,0) in the plane of the Mandelbrot chart. Color shading indicates how fast points outside diverge and points inside converge to zero. The criterion of inside shading can be adjusted with the slider (higher value for less differentiation).
For all points c the Julia set is the green rim of the fractal. Blue areas are those of fast, red those of slow divergence or convergence to zero, and do not belong to the set. The slider varies the gradation of shading. This gives additional insight into the convergence landscape and increases the aesthetic beauty of the fractal structures. Shift the slider at high resolution!
Most impressive large scale structures are calculated for points at the rim or outside of the Mandelbrot fractal. Yet at high resolution the apparently simple structure for points inside reveals interesting fine structure, recalling that of coastal lines or of natural surfaces.
This simulation is part of
“Learning and Teaching Mathematics using Simulations
– Plus 2000 Examples from Physics”
ISBN 978-3-11-025005-3, Walter de Gruyter GmbH & Co. KG
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits

![]() Dieter Roess - WEH- Foundation; Tan Wei Chiong; Loo Kang Wee; Francisco Esquembre ; Wolfgang Christian
Dieter Roess - WEH- Foundation; Tan Wei Chiong; Loo Kang Wee; Francisco Esquembre ; Wolfgang Christian
end faq
Sample Learning Goals
[text]
For Teachers
This is a simulation of a Mandelbrot Set, along with its corresponding Julia Set.
The graph on the left shows the Mandelbrot Set, while the graph on the right shows the corresponding Julia Set of the complex number c, denoted by the white dot on the Mandelbrot Set.
The Mandelbrot Set is a set in the complex plane formed by the recursive equation:
, where z and c are complex numbers.
For a Mandelbrot Set, z(0) is defined to be 0, while c is an arbitrary point in the complex plane. The Mandelbrot Set is defined by the set of values of c where the absolute value of z, |z| does not escape to infinity when run through the above iteration.
For example, take c = 1. The iteration goes as follows:
z(1) = z(0)^2 + 1 = 0^2 + 1 = 1
z(2) = z(1)^2 + 1 = 1^2 + 1 = 2
z(3) = z(2)^2 + 1 = 2^2 + 1 = 5
z(4) = z(3)^2 + 1 = 5^2 + 1 = 26
z(5) = z(4)^2 + 1 = 26^2 + 1 = 677
.
.
.
As this shows, the absolute value of z very quickly inflates to infinity in just a few iterations. Therefore, c = 1 is not part of the Mandelbrot Set.
Now let us look at c = -1. The iteration will go as follows:
z(1) = z(0)^2 + 1 = 0^2 + (-1) = -1
z(2) = z(1)^2 + 1 = (-1)^2 + (-1) = 0
z(3) = z(2)^2 + 1 = 0^2 + (-1) = -1
z(4) = z(3)^2 + 1 = (-1)^2 + (-1) = 0
z(5) = z(4)^2 + 1 = 0^2 + (-1) = -1
.
.
.
Since the iteration oscillates back and forth between z = 0 and z = -1, the absolute value of z for c = -1 does not tend to infinity. We say that |z| is bounded by a finite value.
Therefore, c = -1 is part of the Mandelbrot Set.
The shape formed by the Mandelbrot Set is also a fractal, where zooming in to the boundary of the shape formed by the set reveals repeating patterns of equal or increasing complexity as the magnification increases.
On the other hand, a Julia Set is formed by fixing the value of c as an arbitrary complex number rather than fixing z = 0. The same recursive equation is run, and the conditions that form the set remain unchanged, but the pattern that emerges changes depending on the value of c that is set.
The degree of divergence or convergence to zero is indicated by colour shading. Its gradation can be changed by a slider, labelled internal convergence, which produces interesting colour schemes.
The colours of the two sets can be changed with the combo box. Available colours are:
- Mixed Colours
- Red
- Green
- Blue
Research
[text]
Video
[text]
Version:
- http://weelookang.blogspot.sg/2016/02/vector-addition-b-c-model-with.html improved version with joseph chua's inputs
- http://weelookang.blogspot.sg/2014/10/vector-addition-model.html original simulation by lookang
Other Resources
[text]