About
Monte Carlo methods are often useful for solving problems in physics and mathematics, which cannot be solved by analytical means.
The goal of this virtual-lab is to obtain an approximated value of PI, using a Monte Carlo method. Next, we describe briefly how this method is used to estimate PI.
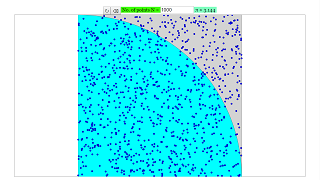
Imagine that we are throwing a dart over a square surface of side 1 m. There is a circle of radius 1 m. inscribed in the square. Assuming that the probability is uniformly distributed, the probability of hitting inside the circle is equal to PI/4. Dividing the number of hits by the number of throws, it is obtained an estimation of PI. We will obtain a better approximation by increasing the number of throws.
This virtual-lab allows the user to select the number of throws, with a maximum of 10000 throws.
Dpto. de Informática y Automática
E.T.S. de Ingeniería Informática, UNED
Juan del Rosal 16, 28040 Madrid, Spain
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits

Carla Martn; Tan Wei Chiong; Loo Kang Wee
end faq
Sample Learning Goals
[text]
For Teachers
Before, we had a simulation on the calculation of π using Archimedes' algorithm. This simulation shows yet another method that can be used to approximate the value of π.
The Monte Carlo method is done by taking a unit square (a square of length 1) and inscribing a quadrant inside. A arbitrary number of points is then randomly scattered in the square. Since the area of the square is 1 and the area of the inscribed quadrant is π/4, the ratio of the number of points that land in the quadrant to the total number of points becomes an estimate of π/4, which is then multiplied by 4 to estimate π.
This method is used widely in mathematics and physics when a problem cannot be solved analytically.
The number of points can be set up to 50000 points. Hit the randomize button to randomize the placement of the points.
Research
[text]
Video
[text]
Version:
- http://weelookang.blogspot.com/2018/05/monte-carlo-pi-calculation-javascript.html
- http://www.euclides.dia.uned.es/simulab-pfp/curso_online/cap7_caseStudies/sec_MonteCarloPI.htm by Alfonso Urquia and Carla Martin-Villalba
Other Resources
[text]