About
Newtonian orbits and the equivalent one-dimensional problem
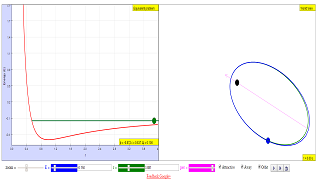
This simulation solves Kepler's problem for the Newtonian potential V(r) = -k/r, mechanical energy E and angular momentum L > 0, in dimensionless variables:- Unit mass is 2-body system's reduced mass m.
- Unit length is the position of the minimum of the effective potential energy in the attractive case (i.e., the radius of the circular orbit): r0 = L2/m|k|.
- Time unit is L3/mk2.
- In these unit we have m = L = |k| = 1, the orbit equation is 1/r = ε cos(φ-φ0) + η with η = |k|/k. The eccentricity is ε = (1+2E)1/2, the effective potential energy -η/r+1/2r2 and its minimum is at point (1,-1/2) for attractive forces.
- If Orbit is selected, along with the orbit one can see the conserved Laplace-Runge-Lenz vector, which goes through the pericentron.
-
To get information on one element, put over it the mouse pointer to
see the corresponding tooltip.
Activities
-
On the left one can see the effective potential energy corresponding
to the equivalent one-dimensional problem (in red).
- Use the mouse (or the corresponding numerical entries) to change the mechanical energy E and the initial value of the polar distance r: the polar angle φ (phi in the simulation) will be set automatically.
- Discuss the values of the eccentricity ε (e) and the form of the orbit for different values of E.
- Uncheck Attracting and discuss what happens with repulsive forces.
- Change orbit's spatial orientation by choosing the pericentron position φ0 (called per in the simulation) or use the following procedure.
- The plane relative motion is displayed on the right. Use the mouse to select the initial position and the orbit orientation.
- With the simultaneous evolutions in the double display you can check that the return points of the one-dimensional problem correspond in the full problem to apses, where the velocity does not vanish, but is perpendicular to the radius.
It requires Java 1.5 or newer and was created by Juan M. Aguirregabiria with Easy Java Simulations (Ejs) by Francisco Esquembre. I thank Wolfgang Christian and Francisco Esquembre for their help.
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits

Juan M. Aguirregabiria (http://tp.lc.ehu.es/jma.html); lookang; tina
end faq
Sample Learning Goals
Students should be able to:
- show an understanding of the concept of a gravitational field as an example of field of force and define the gravitational field strength at a point as the gravitational force exerted per unit mass placed at that point.
- recognise the analogy between certain qualitative and quantitative aspects of gravitational and electric fields.
- recall and use Newton’s law of gravitation in the form \( |F| = \frac{GM_{1}M_{2}}{r^{2}} \)
- derive, from Newton’s law of gravitation and the definition of gravitational field strength, the equation g=GMr2for the gravitational field strength of a point mass.
- recall and apply the equation g=GMr2 for the gravitational field strength of a point mass to new situations or to solve related problems.
- show an understanding that near the surface of the Earth g is approximately constant and equal to the acceleration of free fall.
- define the gravitational potential at a point as the work done per unit mass in bringing a small test mass from infinity to that point.
- solve problems using the equationϕ=-GMrfor the gravitational potential in the field of a point mass.
- analyse circular orbits in inverse square law fields by relating the gravitational force to the centripetal acceleration it causes.
- show an understanding of geostationary orbits and their application.
For Teachers
Video
[text]
Version:
Other Resources
end faq
Facebook Social Comments