About
7.4.3 Energy of a Satellite in circular orbit in terms of distance from Earth, r
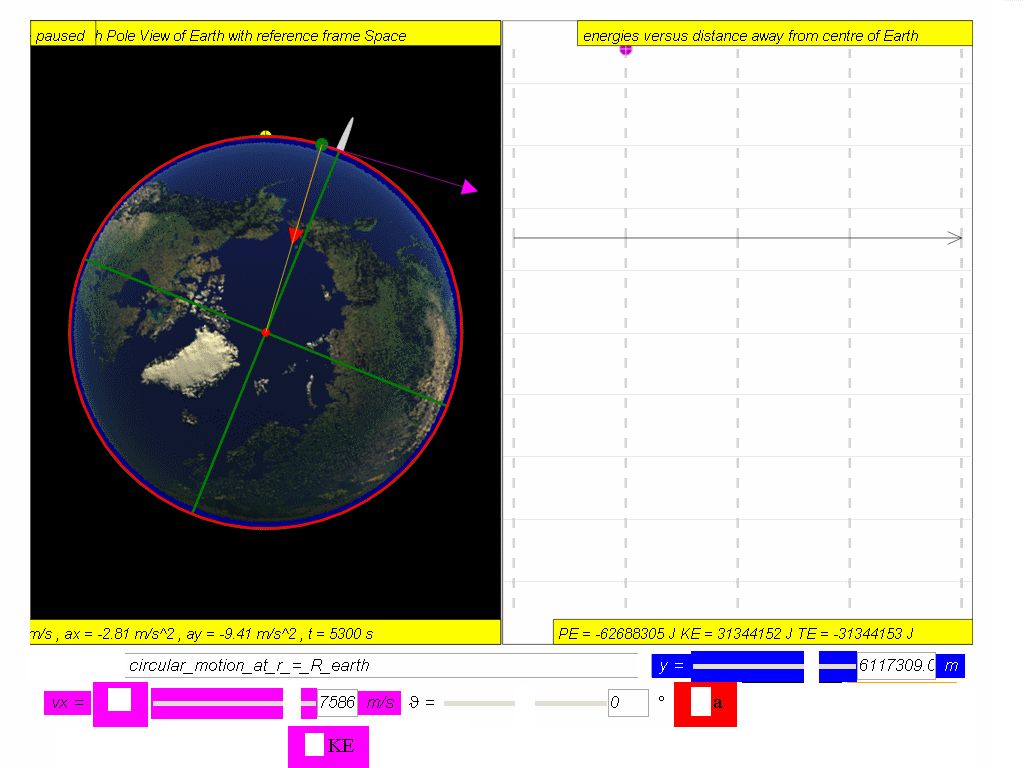
A satellite in orbit possesses kinetic energy, KE, (by virtue of its speed motion) and
gravitational potential energy, PE, (by virtue of its position within the
Earth’s gravitational field).
Hence, total energy of a satellite,
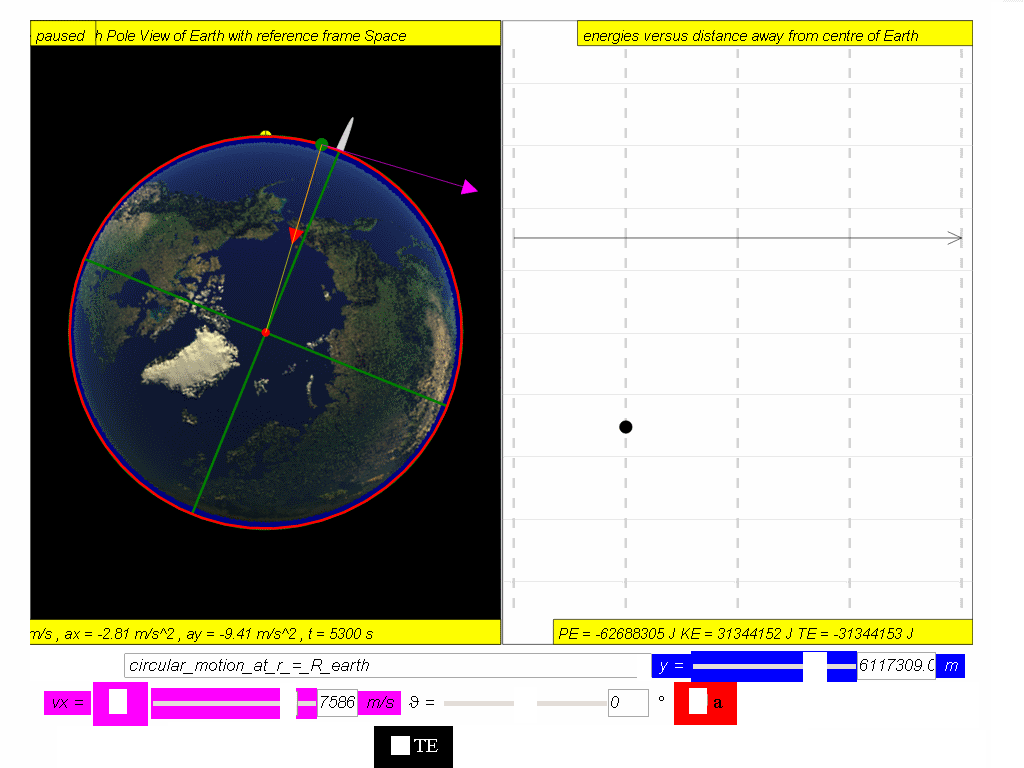
TE = PE + KE
--- Equation (1)
Recall that for a satellite in circular orbit, its gravitational force acts as the centripetal
force:
ΣF = ma
simplifying and multiply by
--- Equation (2)
Substituting equation (2) into (1),
Hence total energy of a satellite, TE = PE + KE
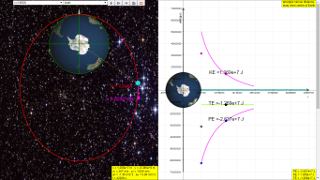
A typical graph showing the relationship between PE, KE and TE with
respect to the distance, r, from centre of Earth, O, is as shown.
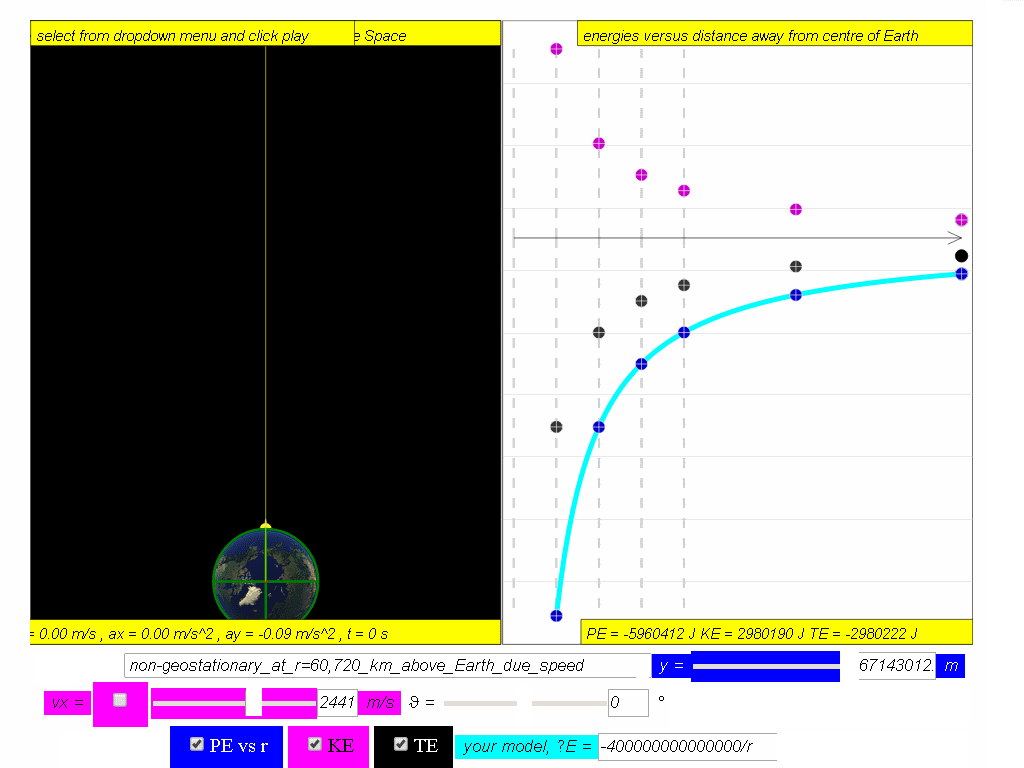
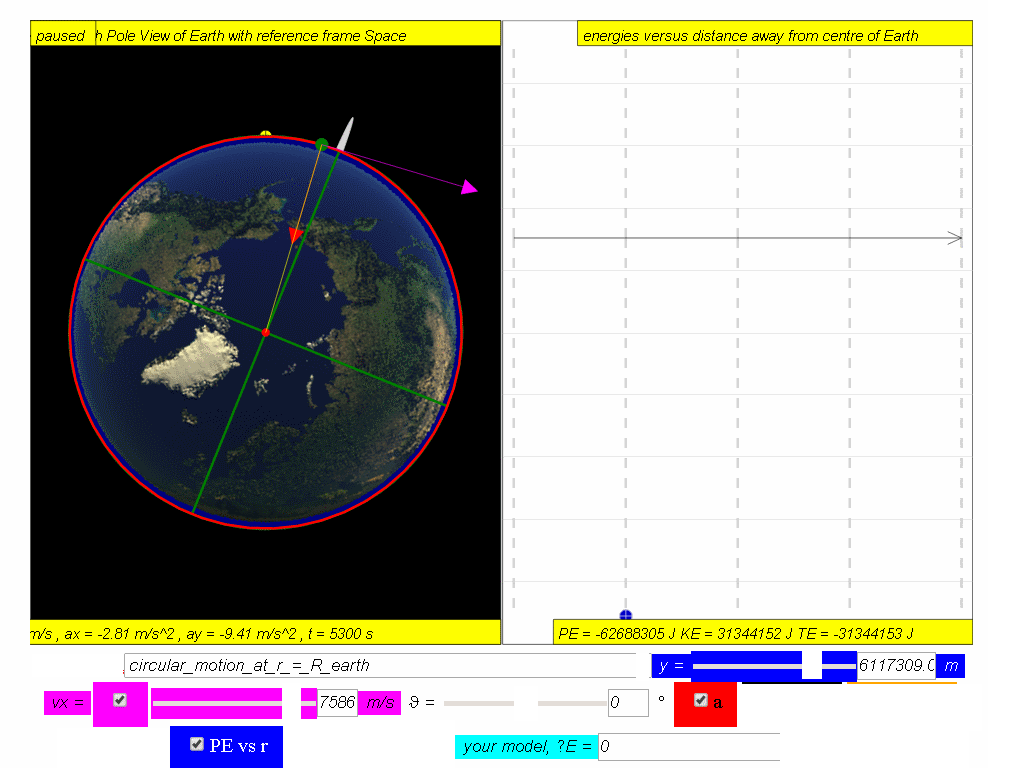
Assuming mass of object mobject = 1kg, Mass of Earth Mearth = 6.0x1024 kg, G =6.67x10-11 N m2 kg-2 , The potential energy PE =
Similarly, determine the equation/model that describes KE and TE and key them into the simulation to test your understanding
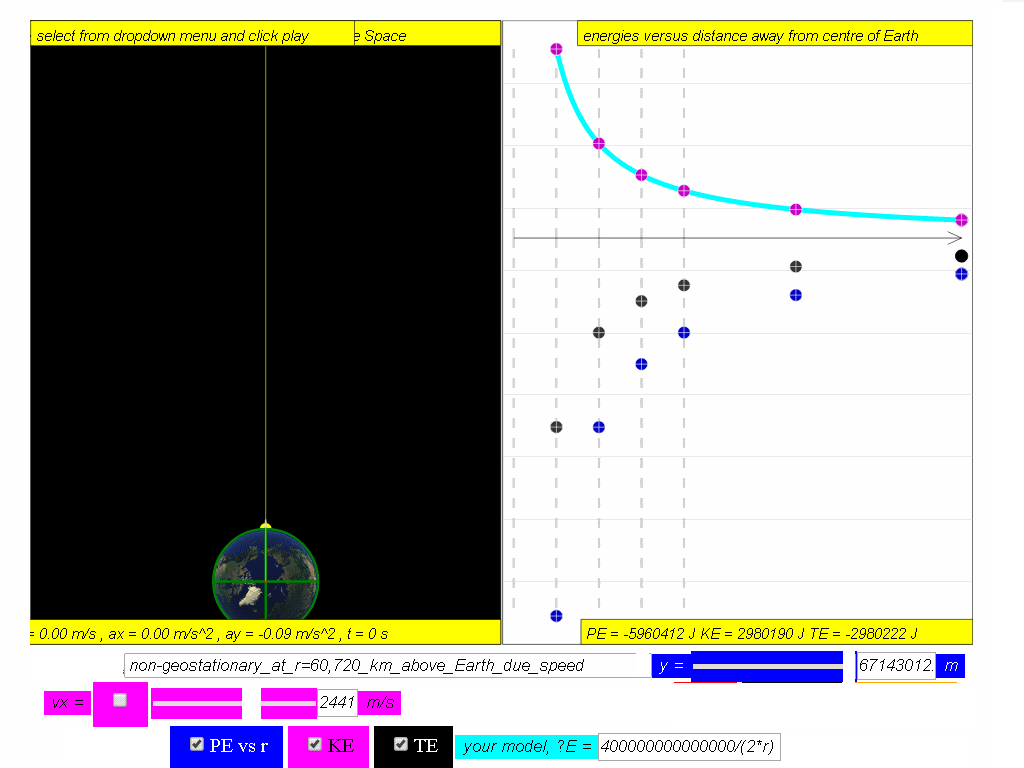
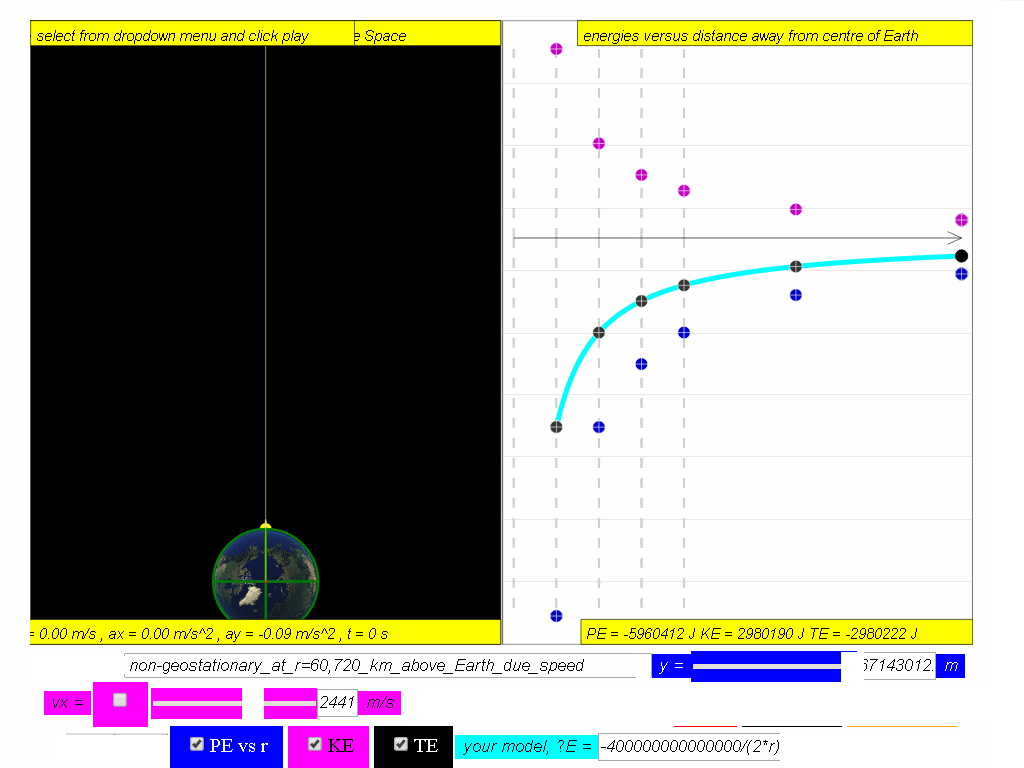
7.4.3.1 Model:
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits
![]()

 Todd Timberlake, this remixed version is by lookang (This email address is being protected from spambots. You need JavaScript enabled to view it.); lookang; fu-kwun hwang
Todd Timberlake, this remixed version is by lookang (This email address is being protected from spambots. You need JavaScript enabled to view it.); lookang; fu-kwun hwang
end faq
App
https://play.google.com/store/apps/details?id=com.ionicframework.gravity081app859103
Versions
- http://physics.weber.edu/schroeder/software/NewtonsCannon.html
- http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejs/ejs_model_NewtonsMountainwee06.jar
Other Resources
- http://physics.weber.edu/schroeder/software/NewtonsCannon.html
- https://scratch.mit.edu/projects/898903/ Launch Simulator by Sushiboy6