About
Gravitational Field
Guiding Questions
- How do two masses interact? Do they need to be in physical contact to do so?
- What do field lines represent? Do field lines represent similar things for gravitational fields and electric fields?
- How can we understand the motion of planets and satellites? Are we at the centre of the universe?
Learning Content of Physics Higher 2 9749_2017
- Gravitational field
- Gravitational force between point masses
- Gravitational field of a point mass
- Gravitational field near to the surface of the Earth
- Gravitational potential
- Circular orbits
Learning Outcomes
Students should be able to:
- show an understanding of the concept of a gravitational field as an example of field of force and define the gravitational field strength at a point as the gravitational force exerted per unit mass placed at that point.
- recognise the analogy between certain qualitative and quantitative aspects of gravitational and electric fields.
- recall and use Newton’s law of gravitation in the form
- derive, from Newton’s law of gravitation and the definition of gravitational field strength, the equation for the gravitational field strength of a point mass.
- recall and apply the equation for the gravitational field strength of a point mass to new situations or to solve related problems.
- show an understanding that near the surface of the Earth g is approximately constant and equal to the acceleration of free fall.
- define the gravitational potential at a point as the work done per unit mass in bringing a small test mass from infinity to that point.
- solve problems using the equationfor the gravitational potential in the field of a point mass.
- analyse circular orbits in inverse square law fields by relating the gravitational force to the centripetal acceleration it causes.
- show an understanding of geostationary orbits and their application.
Learning Experiences Students may have opportunities to:
- Examine the representation used in gravitation. Examine how field lines are useful as a representation of the gravitational field to help in visualising, communicating and deepening the understanding of concepts in gravitation. Discuss the possible limitations of field lines in explaining the various gravitation ideas and concepts as well as possible misconceptions that may arise. Discuss the representation of field lines at surface of the Earth
- Build a model for Newton’s law of gravitation using a simulation Develop a mathematical model for the force of gravitation between two masses using either simulation one or two.
- Investigate the value of g through experiments
Design, carry out and present different experiments 1, 2, 3 (e.g. electromagnetic induction, free fall, oscillations 1,2) to find the value of acceleration of free fall, g. - Explore Newton’s mountain thought experiment on a cannon ball fired at right angles to the Earth’s gravitational field to come to an explanation for orbital motion and escape velocity. The calculated velocity of the cannon ball launched at the top of a mountain (with a height that is negligible when compared to the Earth’s radius) is 7,902 ms−1. This is much greater than the muzzle velocity of modern military cannons, which reach velocities of about 1,800 ms−1. The result is that Newton's Cannon could work in theory, but there is no existing way to fire a cannon ball or any projectile at the velocity required to orbit the Earth.
- Explore how data from satellites is used in Singapore, making reference to the work of the Centre for Remote Imaging, Sensing and Processing (CRISP) and Changi Meteorological Station. Examples of how the data is used by Singapore include the monitoring of the haze 1,2 problem and the prediction of the weather. Students can also compare the differences in the use of data from geostationary orbits satellites and polar orbits satellites for these purposes.
7. Introduction
In the topics of Dynamics, Forces, etc, we have been dealing with weights of different objects. Weight is a name given to the force acting on the object due to gravity. In other words, weight is a gravitational force.
Gravitational force is a force that is evident in our everyday lives and plays a crucial role in many processes on Earth. For instance, the ocean tides are caused by the gravitational attraction of both the Moon and Sun on the Earth’s oceans.
7.0 Real World Physics
7.0.1 Tidal changes over one day
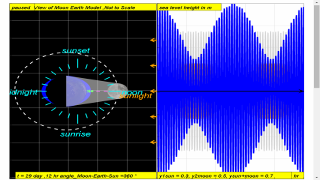
On Day 0, when the Sun, Moon, and Earth form a line (a condition known as syzygy), the tidal force due to the Sun reinforces that due to the Moon. Note the observer experiences high tide.
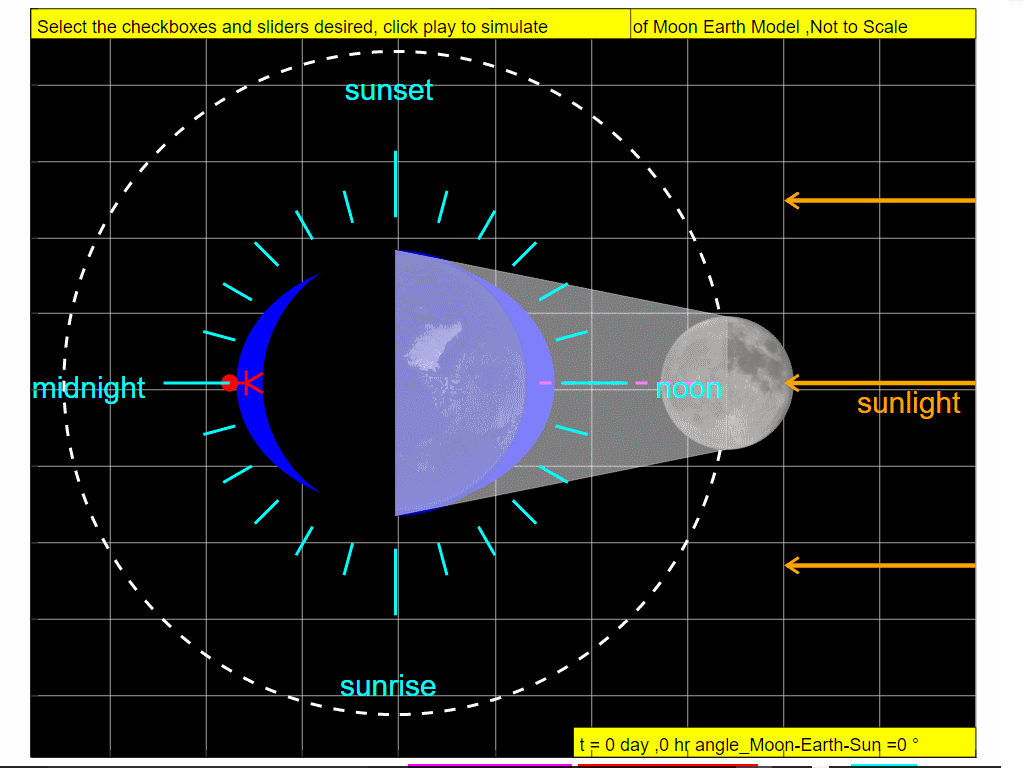
At t =6 hours later, note the observer experiences low tide.
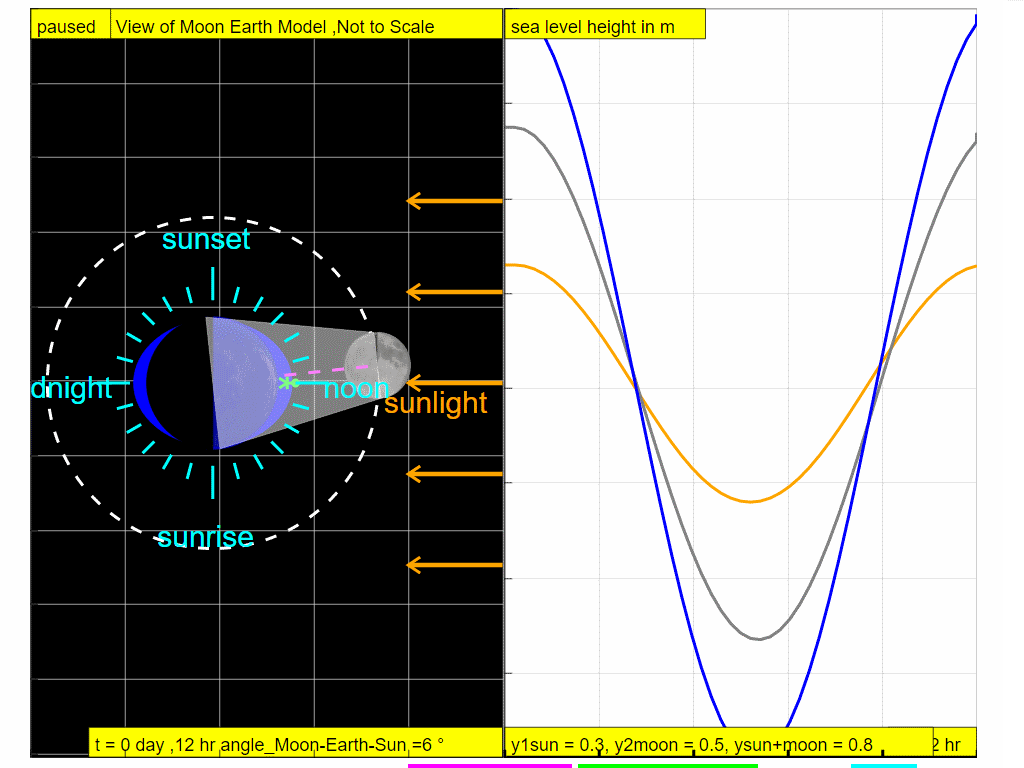
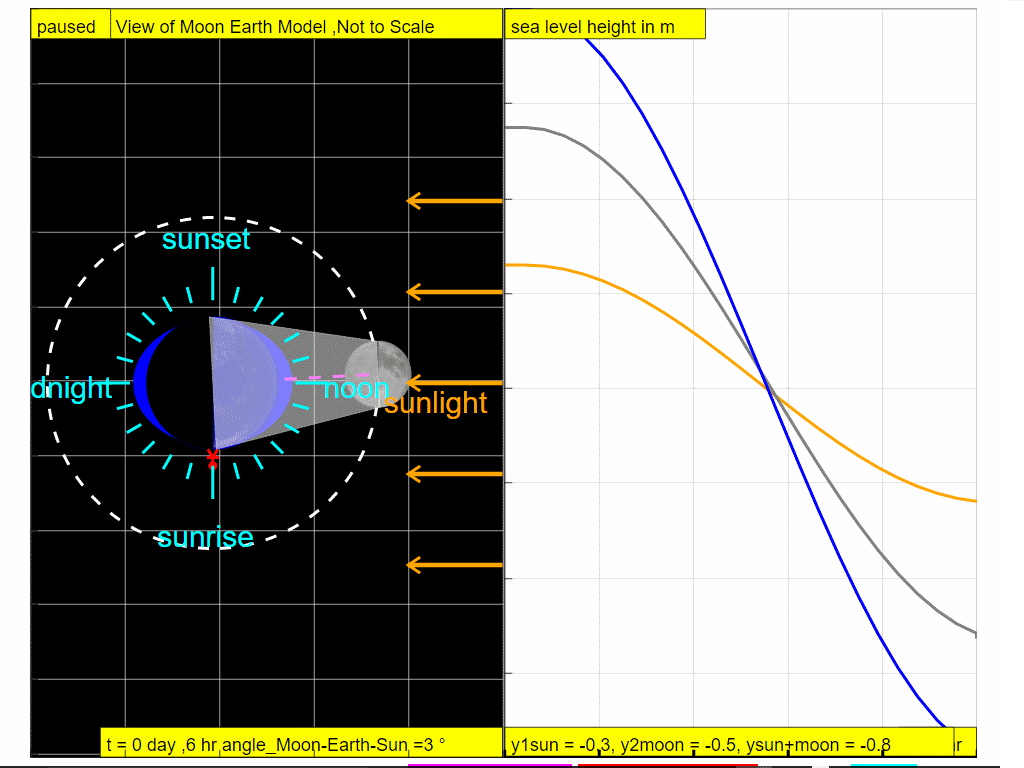
At t =12 hours later, note the observer experiences high tide.
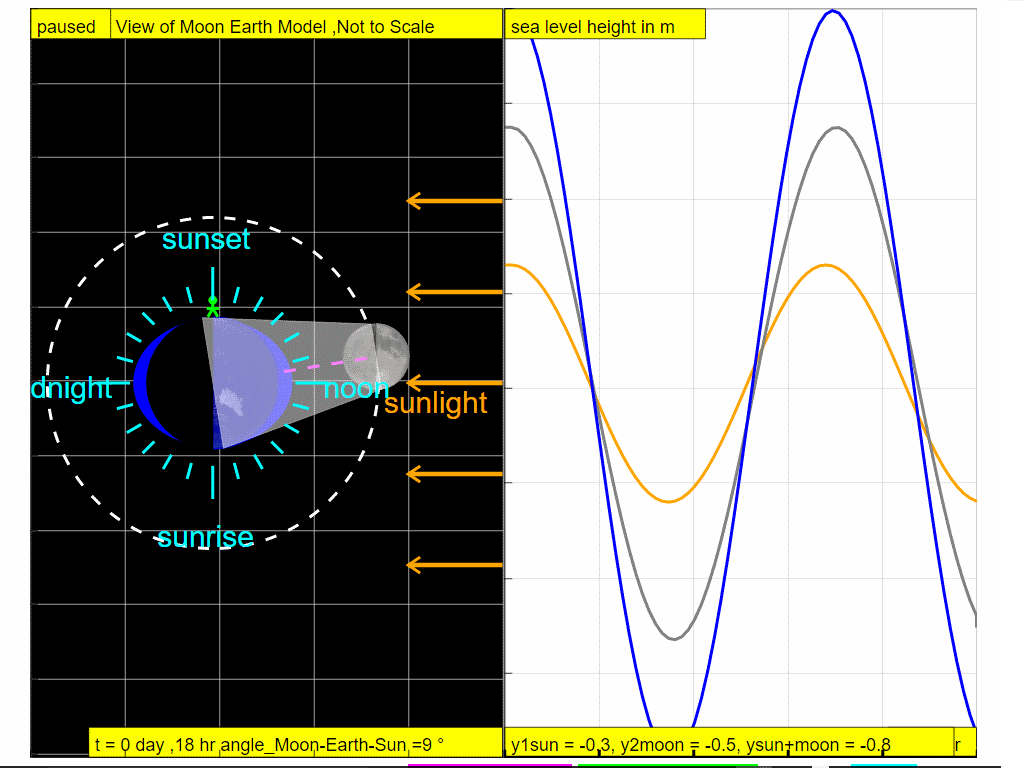
At t =18 hours later, note the observer experiences low tide.
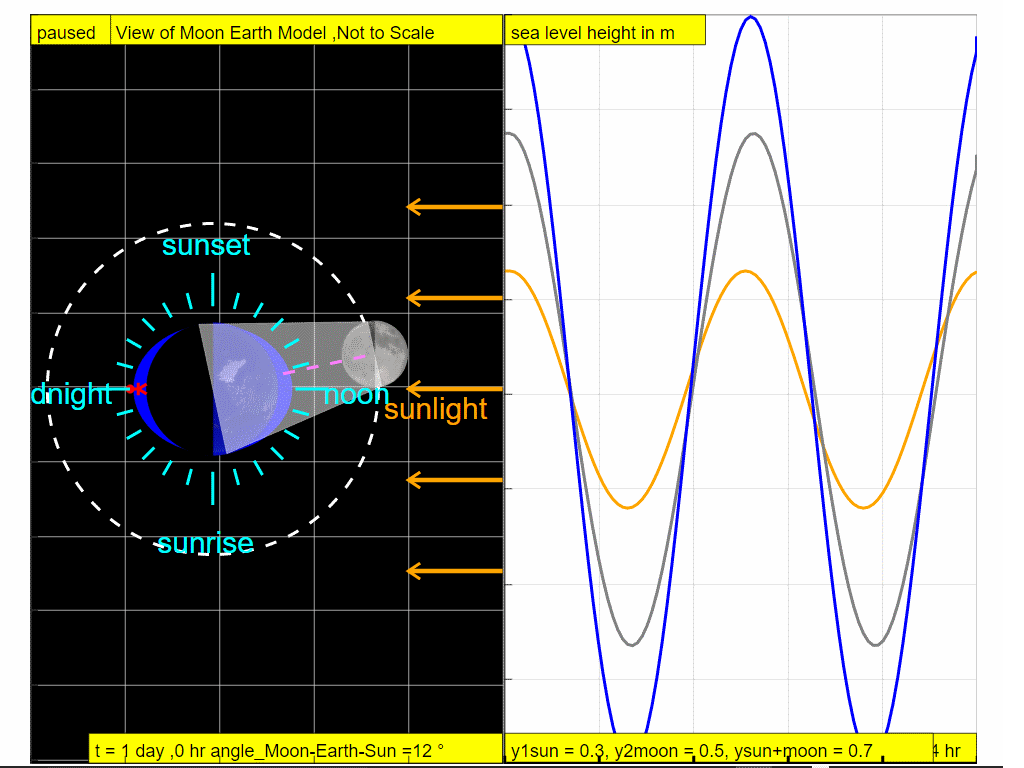
At t =24 hours later, note the observer experiences high tide.
So it can be explained why in approximately one day ( t = 0, 6,12,18 and 24 hours), the combined gravitational forces of the Moon and the Sun give rise to the tidal changes ( high - low - high - low and high respectively).
7.0.2 Tidal changes over one month
At the end of the lunar cycle on the Day 29, 12 hours, around new moon when the Sun, Moon, and Earth form a line (a condition known as syzygy), the tidal force due to the Sun reinforces that due to the Moon. So over 29.5 days, which is a complete lunar cycle, the sea level varies as shown with orange representing the effects of the gravity of Sun, grey representing effects of the Moon and blue representing the resultant sea level waveform. So, gravity physics helps provide a way to formulate an explanation for the formation of tidal changes on Earth.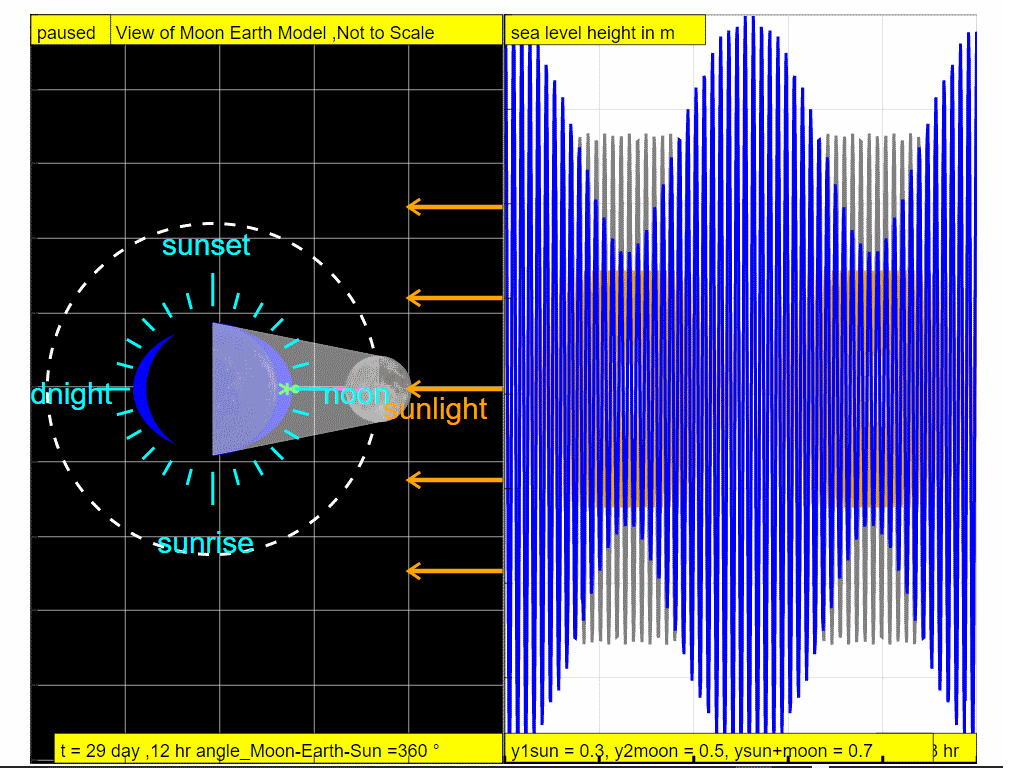
7.0.3 Other phenomena
More visibly around us, the falling of objects when released is also caused by the gravitational pull of the Earth on all objects. In terms of explaining for planetary motion, the same gravitational force is also responsible for keeping the Earth in its orbit around the Sun.
7.0.4 YouTube
- How do tides work? https://youtu.be/5ohDG7RqQ9I
- Reasons for the Seasons https://youtu.be/Pgq0LThW7QA
- What Physics Teachers Get Wrong About Tides! | Space Time | PBS Digital Studios https://youtu.be/pwChk4S99i4
7.0.5 Models:
You may interact with the simulations using the EJSS below link (require internet) or just below if you are using the epub3 reader such as Gitden Reader(Android) or iBook(Apple). It is recommended to enable Scrolling View equal to true by clicking on the AA on the top right corner of the reader app, so as to maximize the view of the simulations.7.0.5.1 Video Tutorial
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits
![]()
 Todd Timberlake; lookang
Todd Timberlake; lookang
end faq
Apps
https://play.google.com/store/apps/details?id=com.ionicframework.gravity01app935489&hl=en
Worksheets
RVHS Lim Ai Phing
YouTube
Research
An Approach for Totally Blind Learners about Day and Night Concepts, M. Şahin BÜLBÜL, Kafkas University / TURKEY
We are happy that
-
bonnie of GIBSON GROUP NEW ZEALAND, working withOtago Museum is going to use this resource. Otago Museum to create an exhibition about the Otago region and the science behind the seasons throughout the year. To create the scenes in the exhibition we need visual content, and we would really like to include your Spring Tide image here: https://en.wikipedia.org/wiki/Tide#/media/File:High_tide_sun_moon_same_side_beginning.png
Other Resources
https://www.geogebra.org/m/A5zD7vJB by Lew W.S.