About
7.3.8.4 Example 9 (J89/II/2)
7.3.8.4.1 Values for the gravitational potential due to the Earth are given in the table below.
| Distance from Earth’s surface / m | Distance from Earth’s centre / m | Gravitational potential / MJ kg-1 | Gravitational Field Strength g / ms-2 | Rate of change of potential with distance / ms-2 |
| 0 | 6 370 000 = 6.37x106= 0.637x107 | -62.72 | ||
| 10 000 000 = 1.0x107 | -40.10 | |||
| 1.363x107 |
2.0x107 | -20.00 | ||
| 3.0x107 | -13.34 | -0.44 |
0.44 |
|
| 4.0x107 | -10.01 | |||
| 5.0x107 | -8.01 | -0.16 | 0.16 | |
| Infinity | 0 |
(i) given that radius of Earth = 6370 km, fill in the missing values in the column of Distance from Earth’s surface / m.
(ii) Calculate the change in potential if an object travels from r = 5.0x107 m to r = 2.0x107 m
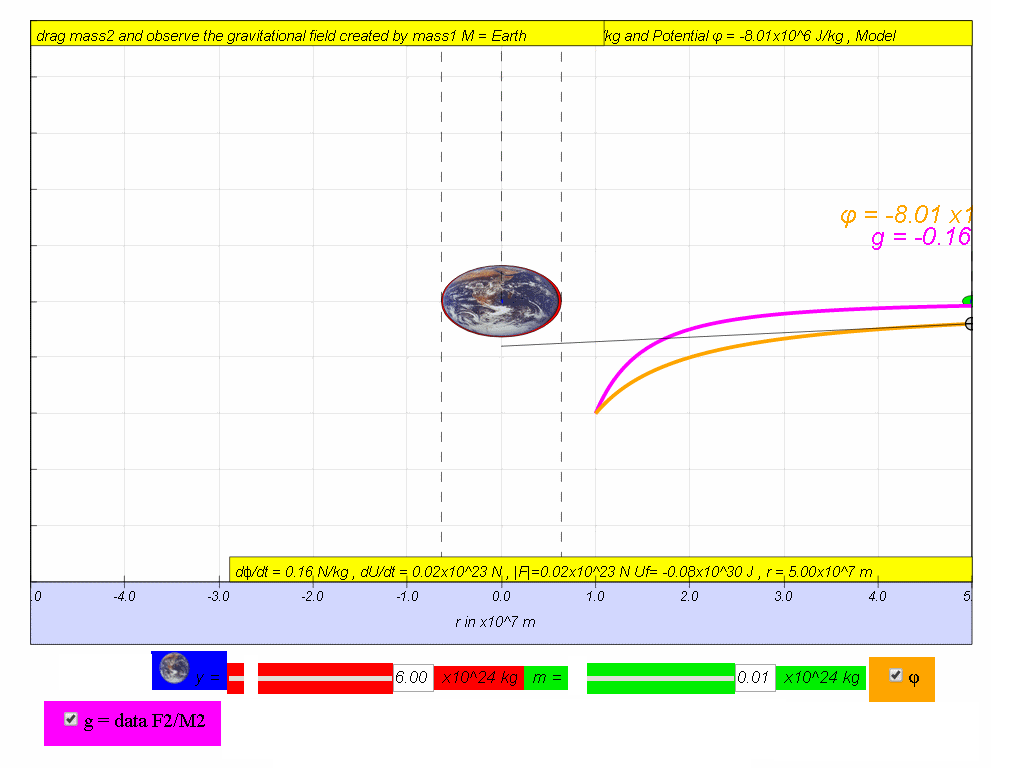
Answer: Δϕ = ϕfinal - ϕinitial = -20.00x106 - (-8.01x106) = -11.95x106 J/kg
(iii) Hence or otherwise, calculate the change in potential energy if the object-satellite has a mass 0.01x1024 kg.
Answer: ΔPE = ΔU = m(Δϕ) = 0.01x1024(-11.95x106) = -1.196x1029 J = -0.20x1030 J
(iv) Determine the potential energy lost by object-satellite of 0.07x1024 kg from a height of 13 630 000 to the Earth's surface.
Answer: ΔPE = m(Δϕ) = 0.07x1024 (-6.67x10-11)(6.0x1024)( ) = (0.07x1024 )(-6.27x107 -(-20.00x107))= (0.07x1024 )(-4.28x107 ) = 2.996x1030 = 3.00x1030 J
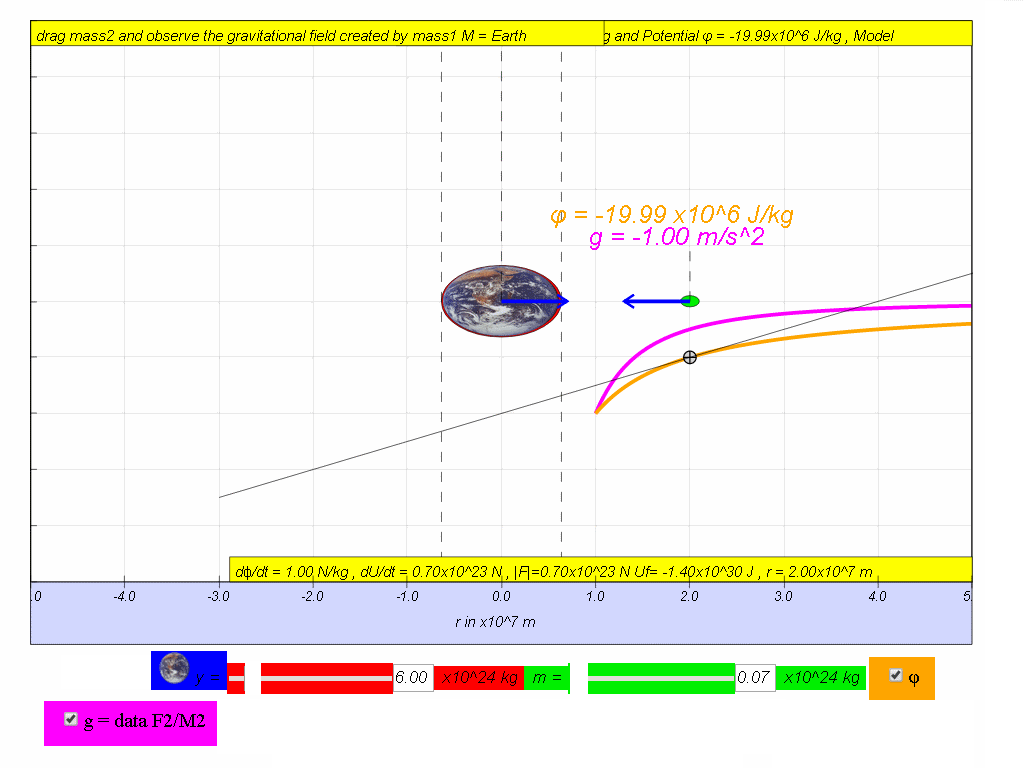
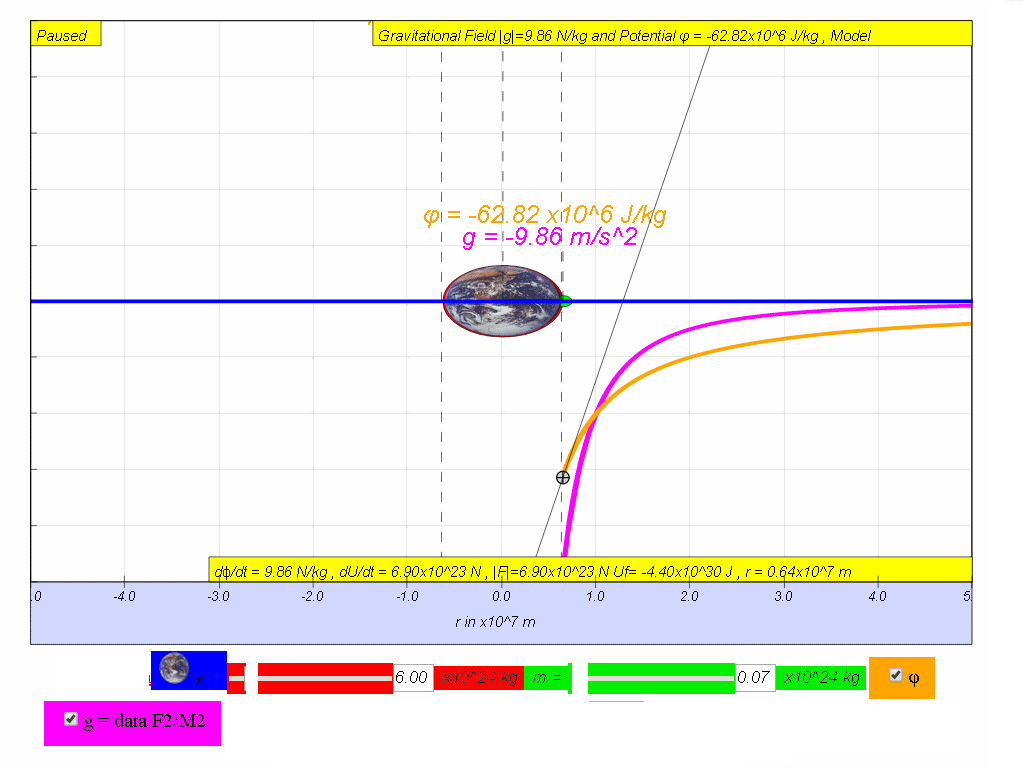
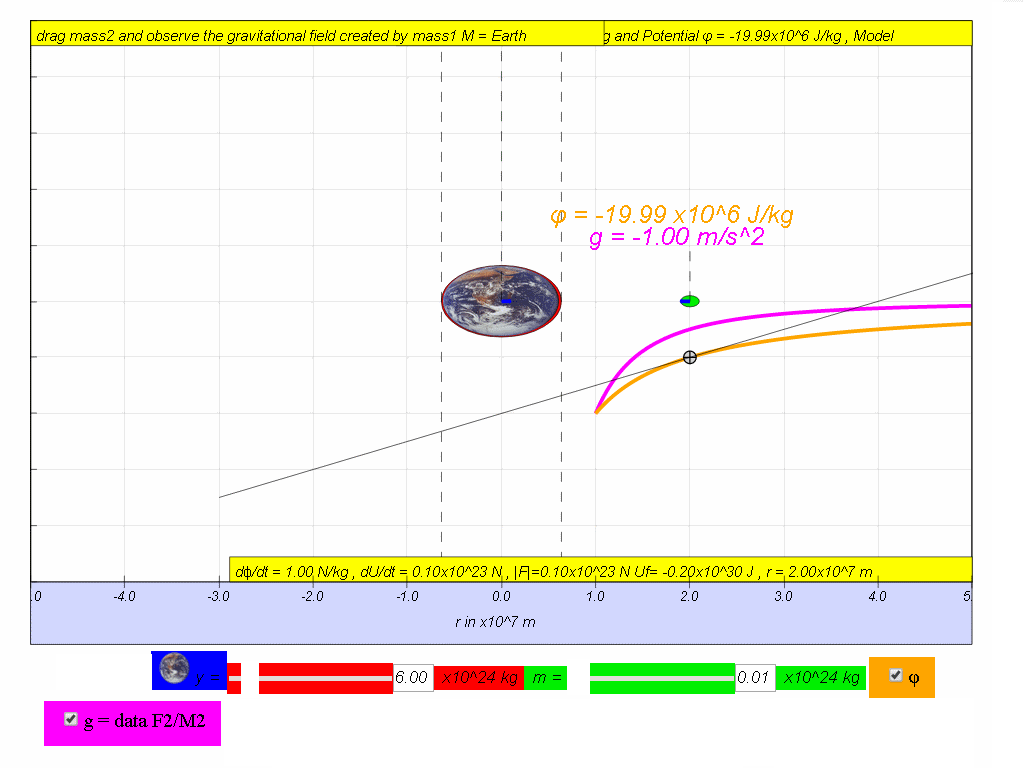
v) by means of using the simulation, move the mass and record down and
fill in the last 2 missing columns for Gravitational Field Strength and
rate of change of potential with distance.
vi) Hence, suggest a relationship between g, ϕ and r.
vii) Explain why the accuracy of determining g at r = 3x107 is poor when using the following values at r = 2x107 and 4x107 m where
7.3.8.4.2 Model
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits
 This email address is being protected from spambots. You need JavaScript enabled to view it.
This email address is being protected from spambots. You need JavaScript enabled to view it.
end faq
Versions
- http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejs/ejs_model_GFieldandPotential1Dv7EarthMoon.jar