About
7.5.2 Geostationary Satellites
7.5.2.1 Introduction
A geostationary (Earth) satellite is a satellite that rotates around Earth in a certain orbit such that it is always positioned above the same point on the Earth’s surface. Hence from the point of view of an observer standing at that point, the geostationary satellite appears to be always ‘stationary’ above him/her (but actually, both observer and satellite are rotating at the same angular speed). In order for a satellite to be moving in such a geostationary orbit, there are certain conditions to meet:
7.5.2.2 Characteristics of Geostationary satellites
- placed vertically above the equator
- same directional sense as the rotation of the Earth (determine through axis of rotation)
- same orbital period of Planet, in our case, Earth, thus the orbital period of approximately 24 hrs
7.5.2.3 Determination of height above Earth surface for geostationary orbit radius.
Analyzing the free body diagram of a satellite traveling in a geostationary orbit, we know the force on the satellite is assumed to be only due to Earth's gravitational pull. The period is approximately 24 hours = (24)(60)(60) = 86400 s
r = 4.23x107 m which is r = 3.59x107 + 6.37x106 m, where radius of Earth = 6.37x106 m.
which is why Earth's geostationary satellites must be placed in an orbit at a fixed distance (around 35 700 km) from the Earth’s surface, in order to rotate with the same period as Earth.
7.5.2.4 Advantages of geostationary satellites:

- A geostationary satellite is ideal for telecommunication purposes since it remains ‘stationary’ above the same spot on the Earth’s surface at all times. The distance between the satellite and the transmitting station on Earth is kept relatively constant and a clear line of ‘vision’ between the transmitter and the receiver allows continuous and uninterrupted signal transmission.
- Since it is always at the same relative position above the Earth’s surface, there is no need to keep adjusting the direction of the satellite dish to receive signals from the geostationary satellite.
- As geostationary satellites are positioned at a high altitude (a distance of 3.57 × 107 m away from the surface of the Earth), it can view a large section of the Earth and scan the same area frequently. Hence, they are ideal for meteorological applications and remote imaging.
7.5.2.5 Disadvantages of geostationary satellites:
- As geostationary satellites are positioned at such a high altitude, the resolution of the images may not be as good as those captured by the lower orbiting satellites (example shown is polar satellites in orbits at r=1.133Rearth with orbital period of 2 hours).
- Because of its high altitude, there may be a delay in the reception of the signals resulting in a lag time for live international broadcasts or video conferences.
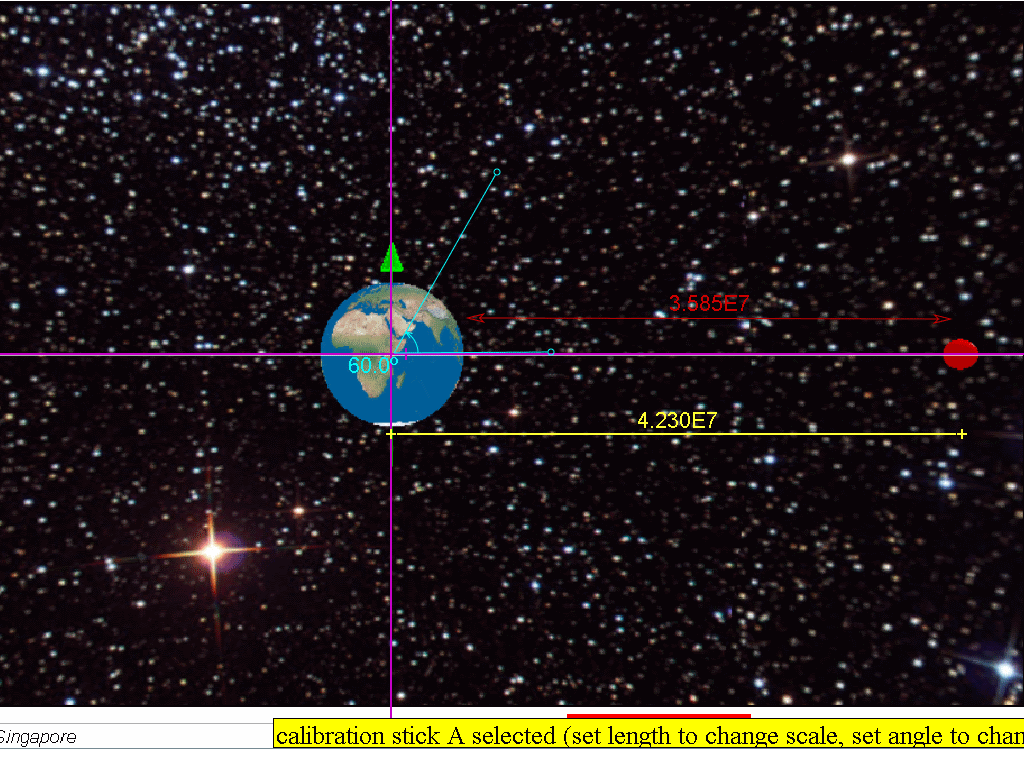 The transmitting
stations in countries positioned at latitudes higher than 60 degrees may
not be able to receive strong signals from geostationary satellites, as
the signals would have to pass through a large amount of atmosphere.
This is true for countries beyond the 60 degrees latitude ‘belt’, both
on north and south sides.
The transmitting
stations in countries positioned at latitudes higher than 60 degrees may
not be able to receive strong signals from geostationary satellites, as
the signals would have to pass through a large amount of atmosphere.
This is true for countries beyond the 60 degrees latitude ‘belt’, both
on north and south sides.
7.5.2.5.1 What are polar orbits?
Besides geostationary satellites which are placed at a large distance from Earth, there are other types of satellite which orbit at lower altitudes from Earth, like the polar orbit satellites as shown below.
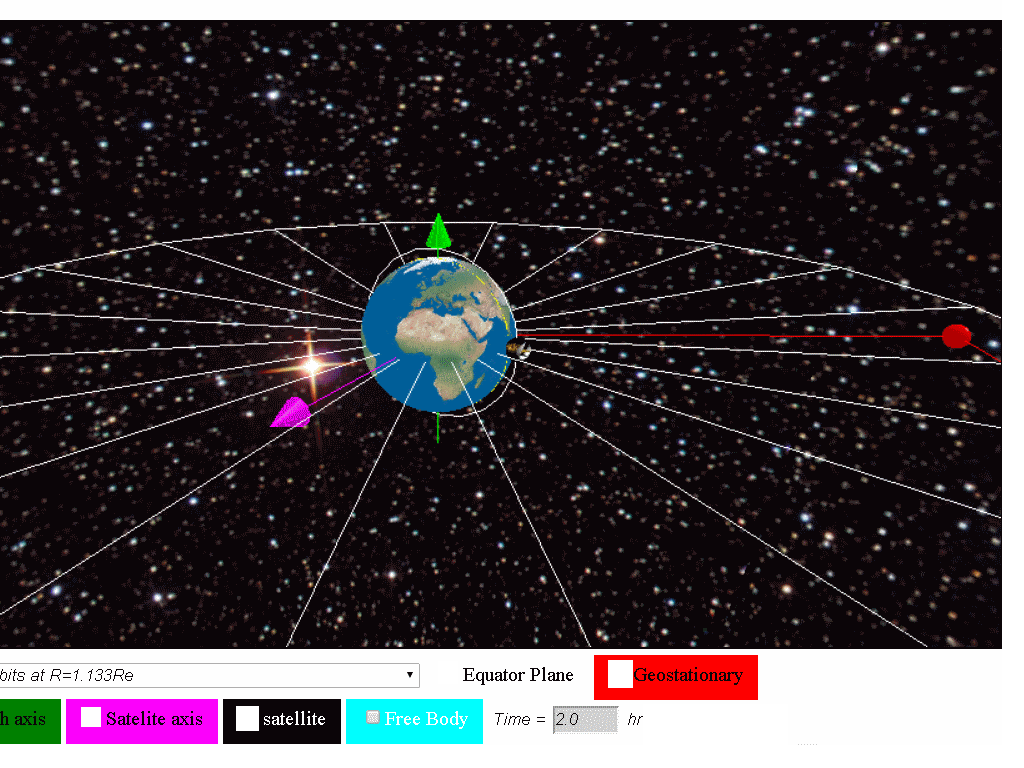
Satellites in polar orbits rotate around the Earth over the poles, in a constant plane perpendicular to the equator. Polar satellites have much lower altitudes (about 850km or R=1.133Rearth with orbital period of 2 hour) which serve to provide more detailed information about the weather and cloud formation. However satellites in this type of orbit can view only a narrow strip of Earth's surface on each passover orbit. Strips of images must be "stitched together," to produce a larger view.
7.5.2.6 Would a geostationary satellite that orbit around planet Mars be at the same distance r = 4.23x107 m ? Why?
referring the data from https://en.wikipedia.org/wiki/Mars, MMars = 6.4185×1023 kg, Sidereal rotation period T =1.025957 day.
r =2.04x107 m,
thus it is different due to the different planet mass and rotation period.
7.5.2.7 Example (J2000/1/8)
Which quantity is not necessarily the same for satellites that are in geostationary orbits around the Earth?A angular velocity C kinetic energy
B centripetal acceleration D orbital period
Answer C: Kinetic energy is dependent on the satellite's mass and velocity. Hence different satellites of different masses may have different kinetic energies.
7.5.2.8 Example
A spacecraft was launched from Earth into a circular orbit around Earth that was maintained at an almost constant height of 189 km from the Earth's surface. Assume the gravitational field strength in this orbit is 9.4 N kg-1, and the radius of the Earth is 6 370 km.a) Calculate the speed of the spacecraft in this orbit.
b) Find the time to complete one orbit.
c) Comment whether this spacecraft is in a geostationary orbit
7.5.2.8.1 Answer:
Since the condition for circular motion is assumed to be true, we can use the circular motion equation while also assuming only the Earth's gravitational force acts on spacecraft.rearranging to get
substituting
7.85x103 m/s = v
b) Since
and
substituting
T = 5249 = 5.25x103 s
c) Since the spacecraft does not satisfy one of the condition (ie. T not 24 hours), it is safe to conclude that the spacecraft cannot be geostationary.
Repeated here are the characteristics of geostationary orbits are:
- placed vertically above the equator
- same direction sense as the rotation of the Earth (determine through axis of rotation)
- same orbital period of Planet, in our case, Earth orbital period of approximately 24 hrs
7.5.2.9 Model
7.5.2.9.1 Geostationary Satellite around Earth Model
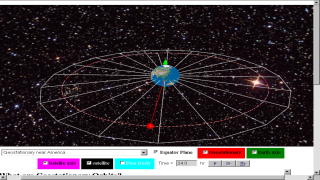
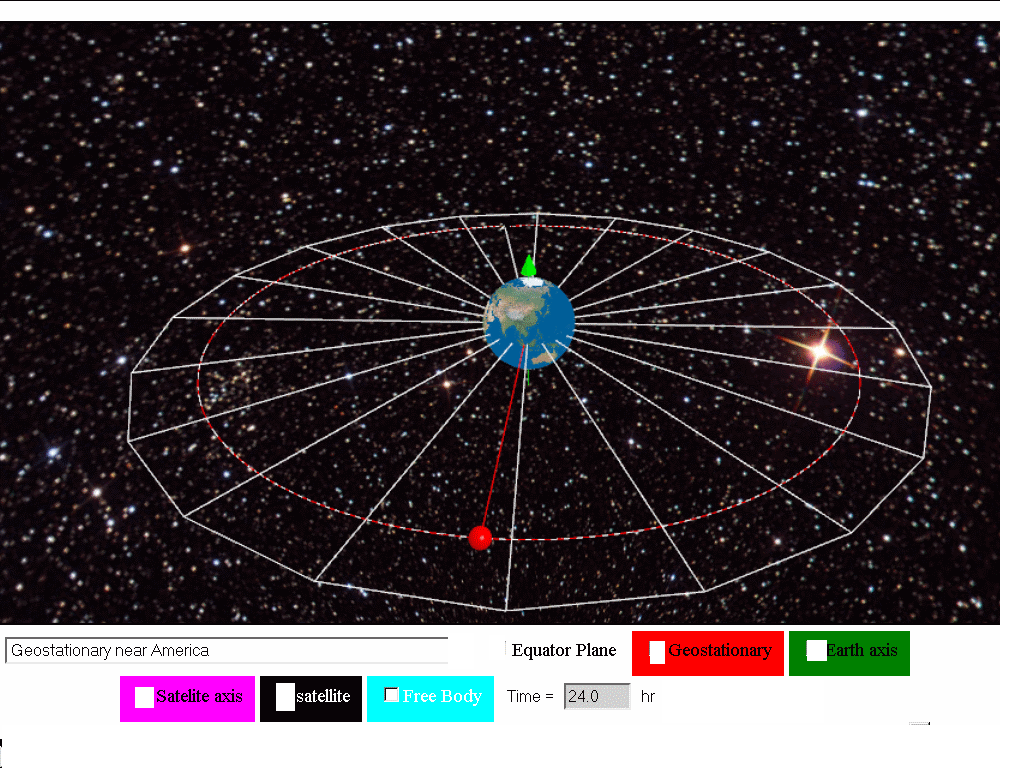
This Geostationary Satellite around Earth Model is a simple angular velocity model that uses the Java3D implementation for realistic visualization of satellite objects in geostationary orbits at three different locations namely (near Singapore, near Africa and America) . Students can explore the meaning of geostationary orbits, cases of non-geostationary orbits and even non-gravity physics orbit .
7.5.2.9.2 Geostationary Satellites
The term Geo-stationary implies a satellite fixed about a position above the earth. This is possible because such satellites have the same period as the Earth’s rotation (T = 24 hours) 2 same rotational sense as the earth's rotation spin 3 is a location directly above the equator in other words the plane of rotation of the satellite must be in the plane of the Equator. Therefore, it appears stationary.
7.5.2.9.3 Application
Example of geostationary satellites are GMS1, GEOS, METEOSAT etc. Most of these satellites are used for commercial and military purposes
7.5.2.9.4 Main Simulation View
The simulation has a Earth and a Satellite object Menu Drop Down Allows for selecting what motion of Satellite is simulated.
- Geostationary near Singapore
- Geostationary near Africa
- Geostationary near America
- Non-geostationary due to direction
- circular motion r=3*Re, T =7.30 hr
- circular motion r=10.5*Re, T = 48 hr
- Non-Geostationary generally
- Unlikely Orbits
7.5.2.9.5 Check boxes
- Show:equator Plane, for visualizing the Earth's rotating equator plane
- Geo stationary, for visualizing a geostationary object (RED) for comparative observation with the other modes.
- Show text: 35 700 km fixed position of object relative to planet earth.
- Axes earth: show spin axes of the rotation of earth in GREEN
- Axes satellite: show spin axes of the rotation of satellite in MAGENTA
- Force: pair of action reaction force of equal magnitude, opposite direction and on different bodies. (Newton's 3rd Law)
7.5.2.9.6 Buttons
- Play
- Step Forward
- Reset
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits

 lookang; Francisco Esquembre
lookang; Francisco Esquembre
end faq
Apps
Video
Press Media
We are delighted to be selected by #ictlt to be interacting with minister ng.
 |
| https://iwant2study.org/ospsgx/index.php/interactive-resources/physics/02-newtonian-mechanics/08-gravity/62-gravity10 |
 Education system should help students become responsible digital learners: Ng Chee Meng
Education system should help students become responsible digital learners: Ng Chee Meng
http://www.channelnewsasia.com/mobile/singapore/education-system-should/2648040.html