About
Developed by A. Titus
Easy JavaScript Simulation by Fremont Teng and Loo Kang Wee
The goal of these exercises is to control a primitive version of an Apollo lander and land on a target on the Moon using vertical and horizontal thrusters. The three thrusters can provide a constant force in the , , and directions, respectively. Only one thruster can be engaged at a time.
Besides modeling the motion of the Apollo lander, the exercises are a “game” in which the user attempts to control the lander and meet the challenge of landing on a given target with minimal speed.

| Subject Area | Mechanics |
|---|---|
| Levels | First Year and Beyond the First Year |
| Available Implementation | Glowscript Easy JavaScript Simulation |
| Learning Objectives | Students will be able to:
|
| Time to Complete | 120 min |
This exercise is named after a late-70s Atari game called Lunar Lander. By employing thrusters in the , , and directions that are aligned with the center of mass of the lander, we do not have to consider rotation. The goal is to control the spaceship using brief impulses. For simplicity, the first two exercises neglect mass loss due to fuel exhaust and are appropriate for introductory students. In Exercises 3-5, students incorporate fuel burn rate. Exercise 5 is intended for intermediate level students who can derive an analytic solution for the y-velocity of a rocket with constant fuel burn rate in a constant gravitational field and can compare numerical and analytic solutions.
Students should view a landing rocket such as the landing of a SpaceX CRS-8 first-stage rocket booster on a floating drone ship.
Students may also want to play the original Atari Lunar Lander game.
Because keyboard interactions are essential to Exercises 1-4, a minimal working program is provided in which the keyboard interactions work, but the lander travels with constant velocity. Students must add the appropriate code inside the while statement to correctly compute the velocity of the lander.
The attached programs are written in GlowScript and require a free account at GlowScript.org.
You will model the motion of a lunar lander and then control the lander so it lands on a given target on the Moon. At first, you will neglect fuel loss. However, this is not realistic, so in later exercises you will include it. Our lunar lander has similar mass and thrust as the Apollo lander, but that’s where the similarities end.
The direction is defined in the direction of the gravitational force by the Moon (downward). The lander has three thrusters that provide a constant thrust in the , , and directions, respectively. Thrust is provided by the expulsion of gases (exhaust). Thus, the righward thrust, showing both the exhaust and the force vector, looks like:
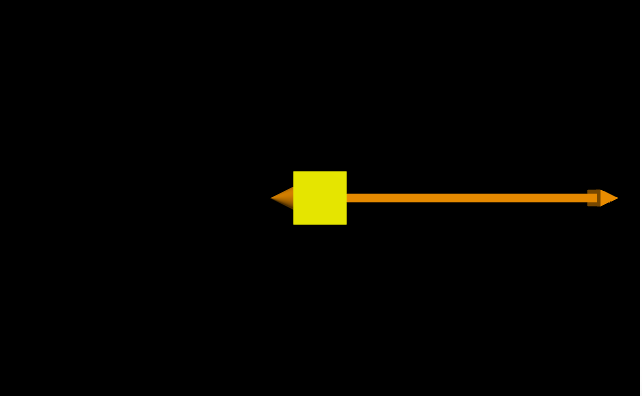
The leftward thrust looks like:
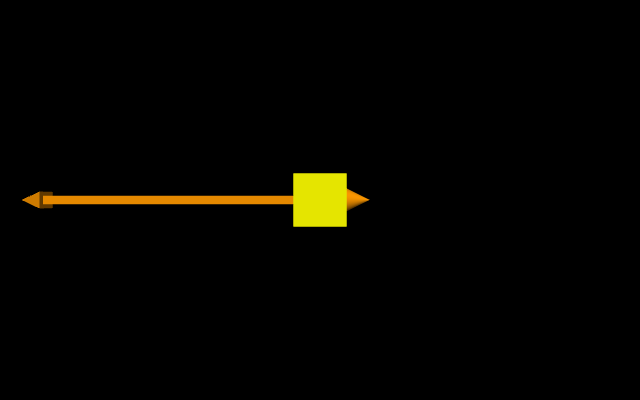
A free-body diagram showing all thrusters engaged simultaneously along with the gravitational force by the Moon is shown below. However, we will assume for these exercises that thrusters cannot be engaged simultaneously. After completing the exercises, you are welcome to explore additional features of your model, such as allowing simultaneous thrusters for example.
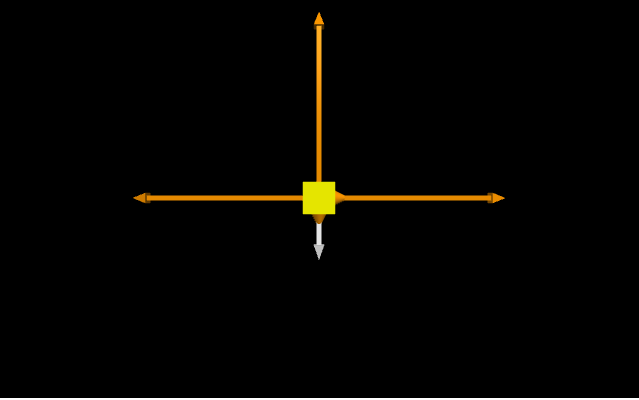
At any instant, the net force on the rocket is
where can be any of the following:
- if no engines are firing.
- if a thruster exerts a force to the right.
- if a thruster exerts a force to the left.
- if a thruster exerts a force upward.
The motion of the rocket is computed using the Momentum Principle:
For speeds much less than the speed of light:
Technically, the expulsion of gases means that the lander loses mass when a thruster is firing. Initially, let’s neglect mass loss due to burning fuel. However, in Exercises 3-5, we will include mass loss due to burning fuel. If including mass loss for the rocket (due to burning fuel), then in each time step:
where is the fuel burn rate in kg/s and is negative. For the special case of a vertically descending or ascending rocket with thruster engaged, an analytic expression for the y-velocity of the rocket can be derived. An analytic calculation can be compared to the numeric calculation for this special case in order to test the computational model.
EXERCISE 1: LANDING ON A GIVEN TARGET
Your goal is to control the lander and land on the target within the safe landing speed and within the safe landing zone.
Use the following parameters:
| Parameter | Value |
|---|---|
| Total initial mass including fuel | kg |
| Initial mass of fuel | kg |
| Fuel burn rate | 0 kg/s |
| Height of lander | 3 m (CM is 1.5 from the bottom of the lander) |
| g | 1.6 N/kg |
| Thrust of an engine | N (3 times the initial weight) |
| Initial velocity | m/s |
| Initial position | m |
| Target position | m |
| Safe landing speed | less than 1 m/s |
| Safe landing zone | m of center of target |
It is best to use keys on the keyboard to turn on or off the thrusters.
Define the position of the lander as its center of mass (CM) position. Define “landing” as when the bottom of the lander reaches the surface of the Moon. Thus, if the lander starts at m and lands with the CM at 1.5 m, then its displacement is actually 48.5 m.
EXERCISE 2: ADDING A THIRD DIMENSION
Add two engines in the directions. Use the following initial conditions for the lander.
| Parameter | Value |
|---|---|
| Initial velocity | (m/s) |
| Initial position | (m) |
Repeat the challenge of landing on the target within the safe landing zone and safe landing speed. You will need to define two more keys to control the two additional engines.
EXERCISE 3: ADDING LOSS OF FUEL
Suppose that the burn rate of fuel is constant and non-zero. This represents the change in mass of the system (lander structure and fuel) per second as an engine is firing. Edit your simulation to include a burn rate of kg/s. If the lander burns all of its fuel, be sure to make the thrust zero. To make the game more interesting, you can increase the absolute value of the burn rate and see if you can land within the safe limits before running out of fuel.
Use your simulation to answer the following questions:
-
As thrusters fire in various directions while you control the lander, does the magnitude of the gravitational force on the lander increase, decrease, or remain the same? Explain your answer.
-
Suppose the vertical thruster is constantly firing for a long time. As it is firing, does the y-acceleration of the lander increase, decrease, or remain the same? Explain your answer.
EXERCISE 4: GRAPHING DATA
Create a graph to plot either or as a function of time. Check your answers to the questions in Exercise 3 by viewing the graph as you operate the lander. Explain whether your answers in Excercise 3 were correct or incorrect and how you determined this.
EXERCISE 5: COMPARING TO AN ANALYTIC SOLUTION
For the simple case of a lander traveling vertically using only its vertical thruster as it lands, you can derive an analytic function for the lander’s y-velocity as a function of time. Use the following initial conditions for the lander.
| Parameter | Value |
|---|---|
| Initial velocity | (m/s) |
| Initial position | (m) |
| Mass burn rate | kg/s |
If the vertical thrust is constant and is engaged during the entire vertical descent, what is the y-velocity of the lander when it hits the surface of the Moon? Solve the problem analytically. Then, simulate it. Compare the numerical result to the analytic result.
What is the necessary minimum speed of the rocket at its initial position m so that firing its vertical thruster for the entire descent will cause the rocket to land with nearly zero velocity?
EXERCISE 1: LANDING ON A GIVEN TARGET
Your goal is to control the lander and land on the target within the safe landing speed and within the safe landing zone.
Use the following parameters:
| Parameter | Value |
|---|---|
| Total initial mass including fuel | kg |
| Initial mass of fuel | kg |
| Fuel burn rate | 0 kg/s |
| Height of lander | 3 m (CM is 1.5 from the bottom of the lander) |
| g | 1.6 N/kg |
| Thrust of an engine | N (3 times the initial weight) |
| Initial velocity | m/s |
| Initial position | m |
| Target position | m |
| Safe landing speed | less than 1 m/s |
| Safe landing zone | m of center of target |
It is best to use keys on the keyboard to turn on or off the thrusters.
Define the position of the lander as its center of mass (CM) position. Define “landing” as when the bottom of the lander reaches the surface of the Moon. Thus, if the lander starts at m and lands with the CM at 1.5 m, then its displacement is actually 48.5 m.
EXERCISE 2: ADDING A THIRD DIMENSION
Add two engines in the directions. Use the following initial conditions for the lander.
| Parameter | Value |
|---|---|
| Initial velocity | (m/s) |
| Initial position | (m) |
Repeat the challenge of landing on the target within the safe landing zone and safe landing speed. You will need to define two more keys to control the two additional engines.
EXERCISE 3: ADDING LOSS OF FUEL
Suppose that the burn rate of fuel is constant and non-zero. This represents the change in mass of the system (lander structure and fuel) per second as an engine is firing. Edit your simulation to include a burn rate of kg/s. If the lander burns all of its fuel, be sure to make the thrust zero. To make the game more interesting, you can increase the absolute value of the burn rate and see if you can land within the safe limits before running out of fuel.
Use your simulation to answer the following questions:
-
As thrusters fire in various directions while you control the lander, does the magnitude of the gravitational force on the lander increase, decrease, or remain the same? Explain your answer.
-
Suppose the vertical thruster is constantly firing for a long time. As it is firing, does the y-acceleration of the lander increase, decrease, or remain the same? Explain your answer.
EXERCISE 4: GRAPHING DATA
Create a graph to plot either or as a function of time. Check your answers to the questions in Exercise 3 by viewing the graph as you operate the lander. Explain whether your answers in Excercise 3 were correct or incorrect and how you determined this.
EXERCISE 5: COMPARING TO AN ANALYTIC SOLUTION
For the simple case of a lander traveling vertically using only its vertical thruster as it lands, you can derive an analytic function for the lander’s y-velocity as a function of time. Use the following initial conditions for the lander.
| Parameter | Value |
|---|---|
| Initial velocity | (m/s) |
| Initial position | (m) |
| Mass burn rate | kg/s |
If the vertical thrust is constant and is engaged during the entire vertical descent, what is the y-velocity of the lander when it hits the surface of the Moon? Solve the problem analytically. Then, simulate it. Compare the numerical result to the analytic result.
What is the necessary minimum speed of the rocket at its initial position m so that firing its vertical thruster for the entire descent will cause the rocket to land with nearly zero velocity?
http://www.glowscript.org/#/user/lookang/folder/Public/program/lunarlander
GlowScript 2.7 VPython
##add keyboard control
def process(event):
global Fthrust
if event.type=='keydown':
k = event.which
if k == 38 and mfuel>0: #up arrow turns on the vertical thruster
Fthrust=thrust*vector(0,1,0)
fireU.visible=True
FarrowU.visible=True
elif k == 39 and mfuel>0: #right arrow turns on the rightward thruster
Fthrust=thrust*vector(1,0,0)
fireR.visible=True
FarrowR.visible=True
elif k == 37 and mfuel>0: #right arrow turns on the leftward thruster
Fthrust=thrust*vector(-1,0,0)
fireL.visible=True
FarrowL.visible=True
elif event.type=='keyup': #releasing the key turns off the thruster
Fthrust=vector(0,0,0)
fireR.visible=False
FarrowR.visible=False
fireL.visible=False
FarrowL.visible=False
fireU.visible=False
FarrowU.visible=False
FthrustArrow.axis=scale*Fthrust
scene=canvas(title="Lunar Lander")
scene.append_to_title("<h2>Instructions</h2>")
scene.append_to_title("<br>1. Click the scene to begin.")
scene.append_to_title("<br>")
scene.append_to_title("2. Hold down the up arrow or right arrow or left arrow to turn the corresponding thruster.")
scene.append_to_title("<br>")
scene.append_to_title("3. Land on the red target. To succeed, the lander's speed must be less than 1 m/s, and it <br>must land within 1 m of the center of the target.")
scene.append_to_title("<br>")
scene.append_to_title("<br>")
scene.bind('keydown keyup', process)
scene.range=40
scene.background=color.black
scene.camera.pos=scene.camera.pos+vector(0,20,-10)
L=3
ground = box(pos=vector(0,-1.1,0), size=vector(50.0,2,50), color=color.white)
lander = box(pos=vector(-10,50,0), size=vector(L,L,L), color=color.yellow)
target = cylinder(pos=vector(10,0,0), axis=vector(0,-1,0), radius=L/2+1, color=color.red)
m_i=1e4
lander.m = m_i
mfuel=8e3
mdot=-500
lander.v = vector(0,0,0)
g=1.6*vector(0,-1,0)
thrust=3*m_i*mag(g)
scale=2*L/m_i/mag(g)
sw=0.5
vstr="Speed: {0:.2f}".format(mag(lander.v))
vlabel=label(pos=vector(0,-10,0), text=vstr)
mfuelstr="Mass of Fuel: {0:.0f} kg".format(mfuel)
mfuellabel=label(pos=vector(-30,-10,0), text=mfuelstr)
fireR=cone(pos=lander.pos-vector(L/2,0,0), radius=L/4, axis=L/2*vector(-1,0,0), color=color.orange, visible=False)
FarrowR=arrow(pos=lander.pos, axis=scale*thrust*vector(1,0,0), color=color.orange, shaftwidth=sw, visible=False)
fireL=cone(pos=lander.pos+vector(L/2,0,0), radius=L/4, axis=L/2*vector(1,0,0), color=color.orange, visible=False)
FarrowL=arrow(pos=lander.pos, axis=scale*thrust*vector(-1,0,0), color=color.orange, shaftwidth=sw, visible=False)
fireU=cone(pos=lander.pos-vector(0,L/2,0), radius=L/4, axis=L/2*vector(0,-1,0), color=color.orange, visible=False)
FarrowU=arrow(pos=lander.pos, axis=scale*thrust*vector(0,1,0), color=color.orange, shaftwidth=sw, visible=False)
Farrowgrav=arrow(pos=lander.pos, axis=scale*lander.m*g, color=color.white, shaftwidth=sw, visible=True)
dt = 0.01
t = 0
Fthrust=vector(0,0,0)
aGraph=graph(title="", xtitle='t (s)', ytitle='a_y (m/s/s)', xmin=0, x=500, y=0, width=400, height=150)
ayPlot=series(color=color.blue, graph=aGraph)
scene.waitfor("click")
while 1:
rate(100)
if(mag(Fthrust)>0):
dm=mdot*dt
mfuel=mfuel+dm
lander.m=lander.m+dm
Fgrav=lander.m*g
Fnet=Fgrav+Fthrust
lander.v =lander.v+Fnet/lander.m*dt
lander.pos = lander.pos + lander.v*dt
if(lander.pos.y-lander.height/2<ground.pos.y+ground.height/2):
print("The lander has landed")
break
t = t+dt
ayPlot.plot(t,Fnet.y/lander.m)
vstr="Speed: {0:.2f}".format(mag(lander.v))
vlabel.text=vstr
mfuelstr="Mass of Fuel: {0:.0f} kg".format(mfuel)
mfuellabel.text=mfuelstr
Farrowgrav.pos=lander.pos
Farrowgrav.axis=scale*Fgrav
FarrowR.pos=lander.pos
FarrowL.pos=lander.pos
FarrowU.pos=lander.pos
fireR.pos=lander.pos-vector(L/2,0,0)
fireL.pos=lander.pos+vector(L/2,0,0)
fireU.pos=lander.pos-vector(0,L/2,0)
if(mag((lander.pos-vector(0,L/2,0))-target.pos)<1):
print("You landed on the target within the allowed landing zone (+- 1 m).")
else:
print("You did not land within the allowed landing zone (+- 1 m). You are "+"{0:.1f}".format(mag(lander.pos-target.pos))+" from the target.")
if(mag(lander.v)<1):
print("You landed on the target within the allowed landing speed (+- 1 m/s).")
else:
print("You landed too fast.")
Exercise 1
There is no right answer, except having a working program and controlling the lander so it lands within the target and within the safe landing speed.
Students should be encouraged to play with the simulation and add game-like elements to it. Landing within the safe landing speed (less than 1 m/s) is fairly difficult.
Exercise 2
In the code template, there is a function def process(event) that handles keyboard interactions. There is a commented line to print the key when it is pressed, as shown below.
k = event . which# print(k)
If this line is uncommented, then you can type any key and get its associated integer. Choose two other keys, like “a” and “s” for example, and edit this function.
In addition, you will want to add cones (for fire) and arrows for the thrust vectors in the z direction.
Exercise 3
It is best to add a graph so you can see how variables such as mass, gravitational force, and acceleration change as thrusters are firing.
- The gravitational force on the lander decreases as thrusters are firing due to the loss of mass.
- The y-acceleration increases as the vertical thruster is firing. The y-acceleration when the vertical thruster is firing is:
As mass decreases due to fuel loss, the denominator decreases less than the numerator decreases. As a result, the fraction increases.
Exercise 4
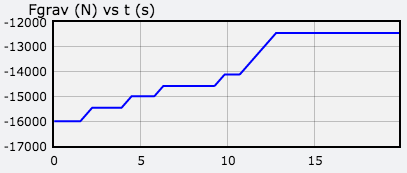
Here is a graph of vs. time. During the flat parts of the graph, the thruster is off. During the upwardly sloped part of the graphs, the vertical thruster is firing and the lander is losing mass.

Here is a graph of vs. time. Each peak corresponds to the vertical thruster firing. It increases as the thruster fires. The flat parts correspond to the engine being off (free-fall). The y-acceleration in free-fall is constant even though the lander loses mass because mass cancels.
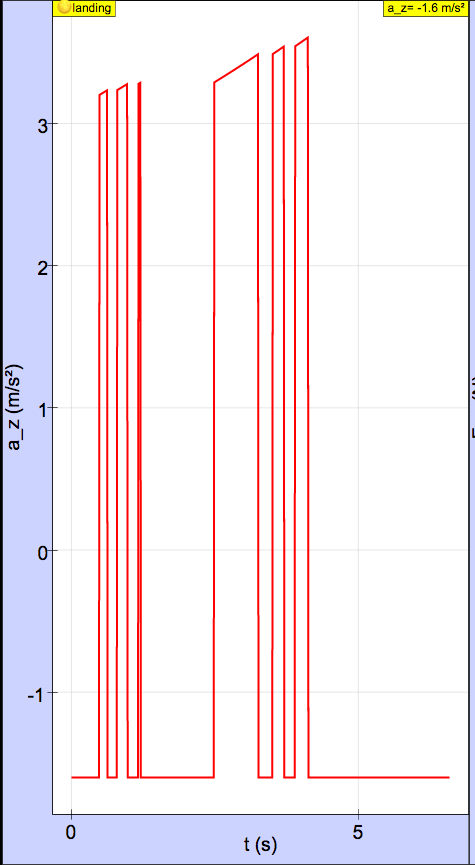
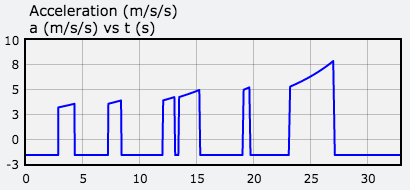
Exercise 5
The y-velocity of a rocket with constant thrust and constant burn rate in a constant gravitational field is:
where is the exhaust speed of the fuel.
With the given initial conditions, the landing speed of the lander computed numerically is 7.000 m/s or 7.17 m/s (Runge Kutta 4 solver in EJSS) and computed analytically is 7.048 m/s. A graph of y-velocity computed numerically (blue) and analytically (red) is shown below. Because the curves overlap, the numerically determined curve is not seen.
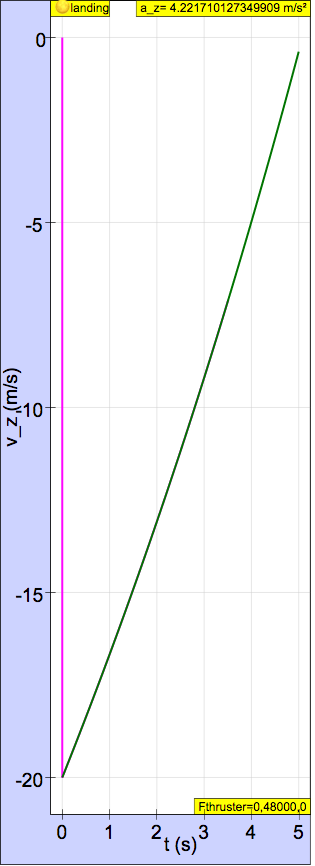
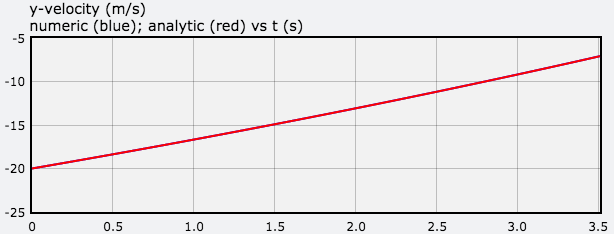
To land with a landing speed less than 1 m/s, the initial y-velocity at a height of 50 m must be -18.88 m/s or -18.86 m/s (Runge Kutta 4 solver in EJSS) .
Chapter 3 in Classical Mechanics by John R. Taylor (University Science Books, 2005).
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits

 Fremont Teng; Loo Kang Wee; based on glowscript by A.Titus
Fremont Teng; Loo Kang Wee; based on glowscript by A.Titus
end faq
Video
[text]
Version:
- https://www.compadre.org/PICUP/exercises/exercise.cfm?I=122&A=lunarlander
- http://weelookang.blogspot.com/2018/07/lunar-lander-game-javascript-simulation.html?m=1
- http://www.glowscript.org/#/user/lookang/folder/Public/program/lunarlander
Other Resources
[text]

.png
)




