About
1.4.3 Example
The mass is displaced to the left from its equilibrium position through a
small distance d and is released. The mass undergoes simple harmonic
motion.
The graph shows the variation with displacement x from the equilibrium
position of the kinetic energy of the mass.
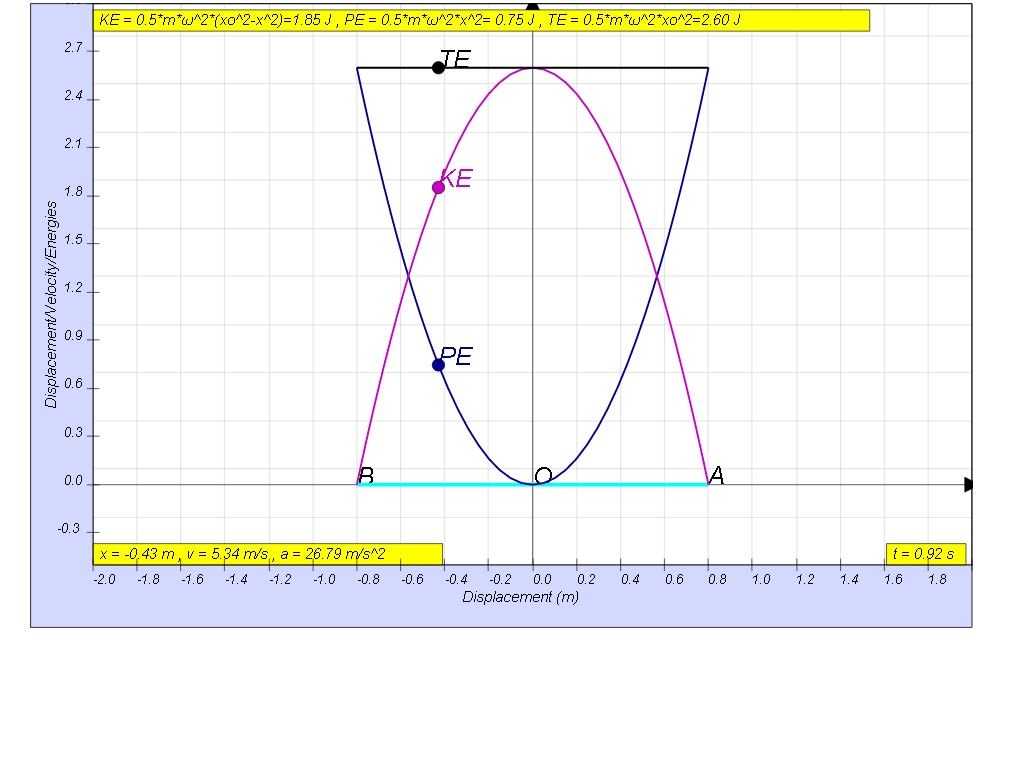
Use the graph to
(a) determine the distance d and the greatest acceleration through
which the mass was displaced initially,
(b) determine the period, frequency and angular frequency.
(c) determine the corresponding equations of displacement, velocity and acceleration.
(d) determine the corresponding equations of elastic potential energy and the total mechanical energy and sketch them on the graph above.
(e) determine the corresponding equations of kinetic energy, potential energy and total energy
[0.8m, 0.79 s, 1.26 Hz, 7.91 rad/s]
[ x= - 0.8 cos(7.91t), v= 6.32 sin(7.91t), a= 50 cos(7.91t)]
[KE = 2.6 sin 7.912t, PE = 2.6 cos 7.912t, TE =2.6 J]
[KE = 4.06 (0.82-x2), PE = 4.06 x2, TE = 2.6 J]
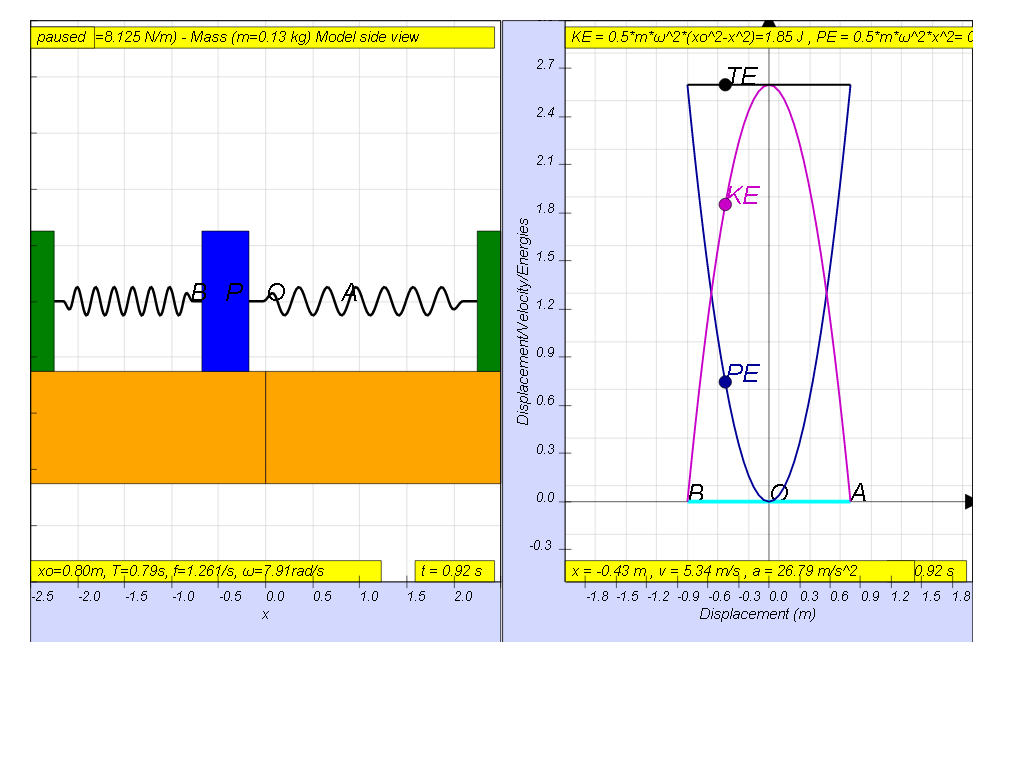
Using the model, this graph can be shown
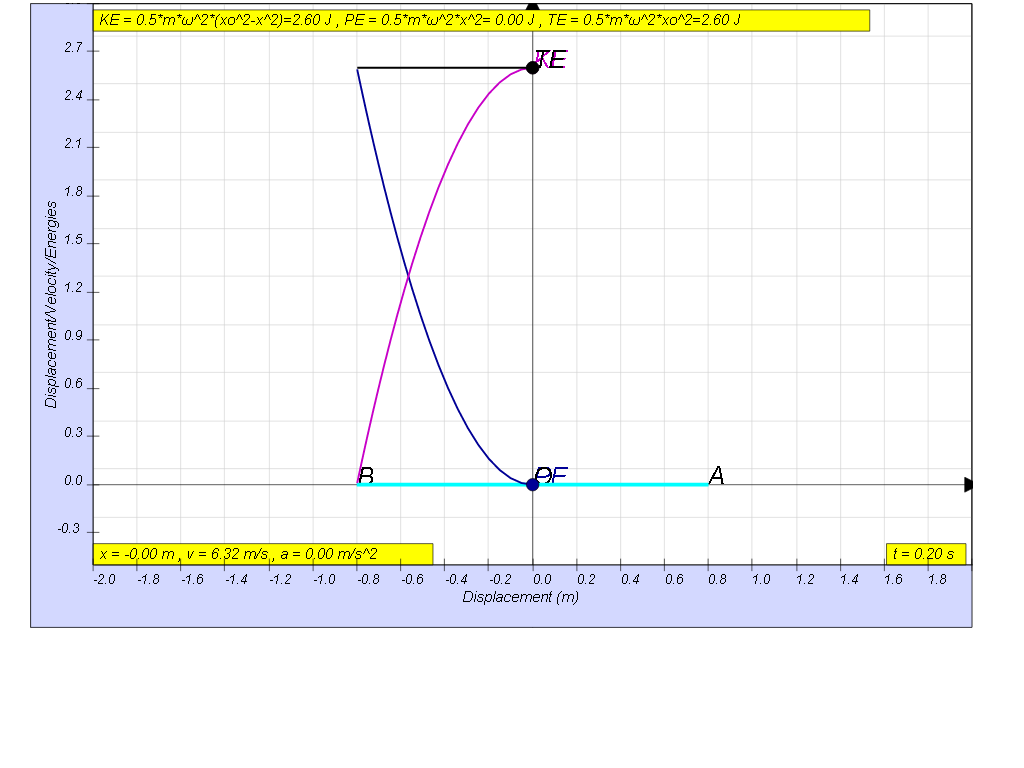
the velocity maximum value can be found in the model as well
1.4.3.1 Model:
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits
 This email address is being protected from spambots. You need JavaScript enabled to view it.
This email address is being protected from spambots. You need JavaScript enabled to view it.