About
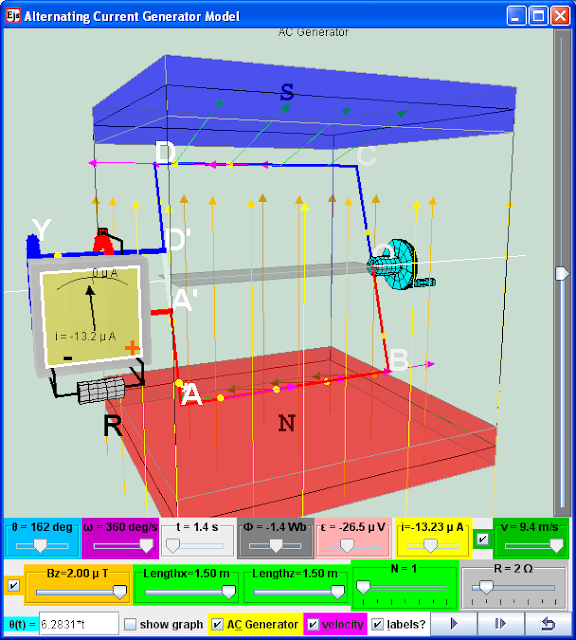
Electric generators turn motion into alternating-current electric power by exploiting electromagnetic induction. A loop that is placed in a magnetic field induces an motional electromagnetic force (emf). A simple alternating current (AC) generator is illustrated here. ABCD is mounted on an axle PQ. The ends of the wire of the loop are connected to 2 brushes contacting two slip rings continuously at position X & Y. Two carbon brushes are made to press lightly against the slip rings.
The motor features a external magnet (called the stator because it’s fixed in place) and an turning coil of wire called an armature ( rotor or coil, because it rotates). The armature induces an emf, because any change in the magnetic environment of a coil of wire will cause a voltage (emf) to be "induced" in the coil.
The key to producing motional emf is in change in the magnetic flux experienced by the coil loop.
Faraday's law states the induced emf in a coil is equal to the negative of the rate of change of magnetic flux times the number of turns in the coil. The induced electromotive force or emf, ε in any closed circuit is equal to the rate of change of the magnetic flux , Φ through the circuit.
|ε| = | d(Φ)/ dt |
where Φ = N.B.A cos ( B&A)
|ε| is the magnitude of the electromotive force (emf) in volts
Φ is the magnetic flux through the circuit (in webers).
N is the number of turns of wire in the loop
B is the magnetic field
A is area of coil
angle B&A is the angle between vector magnetic field and vector perpendicular to the area
Lenz's law states an induced current is always in such a direction as to oppose the motion or change causing it.
The law provides a physical interpretation of the choice of sign in Faraday's law of induction, indicating that the induced emf and the change in flux have opposite signs. The the polarity of the induced emf is such that it produces a current whose magnetic field opposes the change which produces it
ε = - d(Φ)/ dt
For the case of a rotating loop,
ε = - d(Φ)/ dt
From eariler equstion as Φ = N.B.A cos ( B&A)
ε = - d(N.B.A cos ( B&A))/ dt
the physical setup of Bz and normal vector of area A when t = 0 s, such that angle B&A = ( θ + π/2 ).
and taking out the constants from the differential equation,
ε = - N.B.A d( cos ( θ + π/2 )/ dt
from mathematical trigometry identity, cos ( θ + π/2) = -sin ( θ )
ε = - N.B.A d( -sin ( θ )/ dt
To derive an expression for the induced emf across the slip rings when the coil is spun at a angular frequency, ω, knowing θ = ω.t
ε = - N.B.A d( -sin ( ω.t )/ dt )
ε = N.B.A d( sin ( θ )/ dt ) which the equation used by the custom function getCurrent () = d( sin ( θ )/ dt )
When a closed ciruit in connected to the rotating loop, using Ohm's law
ε = N.B.A.d( sin ( θ )/ dt ) = I.R which the equation used by the model
When mechanical energy is used to rotate the loop, the armature induced a emf described by the right hand rule. The induced emf in a coil is equal to the negative of the rate of change of magnetic flux times the number of turns in the coil.
Use the rotating handle function input field θ(t)= _________ to see what happens when the rotating handle cranks the loop in the Bz magnetic field. The checkbox current flow & electron flow alows different visualization since I = d(Q)/dt and Q= number of charge*e. The Play & Pause button allows freezing the 3D view for visualizing these induced currents, for checking for consistency with the right hand rule.
When the rotating handle is moved by the input field θ(t)= 2*t , induced current runs through ABCD (select the checkbox labels?) in a manner described by
ε = N.B.A.ω .cos ( ω.t ) = I.R.
since θ(t)= 2*t , imply 2 = ω
ε/R = N.B.A.ω .cos ( ω.t )/R = I. which is the modeled equation.
If N = 1, B = 2 x10-6 T, A = 1.5*1.5 m*m, R = 1 Ω
ε/R = 1.2.1.5*1.5.2x10-6 .cos ( 2.t )/1 = I.
ε = 9x10-6 cos ( 2.t ) = I
For Teachers
Exercises:
Figure of a Real Life Demo Set by AddeStation Dr KC Tan
1. Explore the simulation; this simulation is designed as an electric generator that turns motion into alternating-current electric power by exploiting electromagnetic induction. This AC generator model consists of 2 pole magnets and a wire (usually a very long one that's wrapped to form several coils and known as an armature or coil). A hydraulic engine or some other outside source of motion (This applet has a handle bar for you to rotate) moves the wire or armature through the external magnetic field created by the magnets.
2 The play button runs the simulation, click it again to pause and the reset button brings the simulation back to its original state.
3 by default values Bz, Lengthx, Lengthz, N, R, ϑ = 6.2831*t play the simulation. Notice ϑ = 6.2831*t is the angular displacement function of the handle bar. The wire is in a rotation motion and the galvanometer display the induced current in the AC generator. What is the physics principle simulated here.
Hint: Faraday's law
4 reset the simulation.
5 using the default values (Bz, Lengthx, Lengthz, N, R,), adjust the value of ϑ = 1*t play the simulation. What did you observe? Explain the motion in terms of the ϑ, ω
6 explore the slider Bz. what do this slider control?
7 explore the slider Lengthx. What does this slider control?
9 together a variable called A is defined as Lengthx*Lengthz, suggest a suitable meaning for A.
11 record down the names of the variables and its meaning from the tips.
10 vary the simulation and get a sense of what it does.
What are the magnetic poles when Bz is positive?
|
Top:
Bottom: |
12 What can you conclude about the directions of the magnetic field exerted by the magnets?
|
|
13 The external magnetic field Bz can be varied using the slider Bz. When Bz is positive, it is in the direction vertically up. Vary Bz until it is negative, what is the direction of the Bz then?
|
|
When θ = 0o What is amount of magnetic flux Φ passing through the area of the coil loop is zero Wb.
15 Step the simulation by dt, take note of the new value of the θ and the new Φ reading. By calculating d(Φ)/ dt, at this instant in time. Think of a way, to collect the data to fill in the following table.
|
θ / deg.
|
t / s
|
Φ / Wb
|
d(Φ)/ dt / Wb/s
|
to be read from the graph
ε / V |
i / A |
|
0
|
|
|
|
|
|
|
18
|
|
|
|
|
|
|
36
|
|
|
|
|
|
|
54
|
|
|
|
|
|
|
72
|
|
|
|
|
|
|
90
|
|
|
|
|
|
|
108
|
|
|
|
|
|
|
126
|
|
|
|
|
|
|
144
|
|
|
|
|
|
|
162
|
|
|
|
|
|
|
180
|
|
|
|
|
|
|
198
|
|
|
|
|
|
|
216
|
|
|
|
|
|
|
234
|
|
|
|
|
|
|
252
|
|
|
|
|
|
|
270
|
|
|
|
|
|
|
288
|
|
|
|
|
|
|
306
|
|
|
|
|
|
|
324
|
|
|
|
|
|
|
342
|
|
|
|
|
|
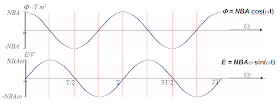
The _________ and ______________ of the induced current _____________ as the coil rotates. This is the basic principle behind the simple AC generator.(c) Sketch a graph of voltage output against time for a simple a.c. generator
Using default starting values of the simulation, play the simulation until at θ = 0 degree again at t > 0.0 s
What is the direction of the current flow in wire AB?
Please submit your remix model that model features that are not available in the existing virtual lab and share your model with the world through NTNUJAVA Virtual Physics Laboratory http://www.phy.ntnu.edu.tw/ntnujava/index.php?board=28.0. Impacting the world with your model now.
Lecture note on Ac Generator in JC
16.7 Simple Applications of EM Induction
16.7.1 A.C. Generators
Alternating current (a.c.) generators are devices that convert mechanical energy to electrical energy. In its simplest form, it consists of a loop of wire rotated by some external means in a magnetic field (as shown in the diagram below). In commercial power plants, the energy required to rotate the loop can be derived from a variety of sources (e.g. for hydroelectric plant, falling water is directed against the blades of a turbine to produce the rotary motion).
• The magnitude of the e.m.f. is given by:
If the coil is turning at a constant rate, then θ = ω.t where ω = the angular frequency.
Note:
• The maximum magnitude of the e.m.f. is equal to when the coil is parallel to the field B ( vector A is 90 deg to notes θ) which in the applet case are angle θ = 0 and 180 deg but the notes θ = 90 and 270 deg
Video
by Ejs Open Source AC Generator Model Java Applet by lookang lawrence wee
Ejs Open Source Alternating Current Generator Model Java Applet ( AC Generator ) v2011feb by lookang lawrence wee
AC Generator by Michael Melloch
How AC Generator Produces Electricity? - Physics || Extramarks
Software Requirements
Java
Credits
Fu Kwun Hwang and Loo Kang Wee
Versions
- http://iwant2study.org/lookangejss/05electricitynmagnetism_22electromagneticinduction/ejs/ejs_model_ACgenerator07.jarby Fu-Kwun Hwang and Loo Kang Wee Java version
- http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=1275 by Fu-Kwun Hwang and Loo Kang Wee Java version
- http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=915.0 by Fu-Kwun Hwang
- http://www.compadre.org/OSP/items/detail.cfm?ID=9218&Attached=1 different Electric Generator Model by Anne Cox and Wolfgang Christian
Other Resources
- http://www.walter-fendt.de/ph14e/generator_e.htm by Generator Java version byWalter Fendt
- http://micro.magnet.fsu.edu/electromag/java/generator/ac.html AC Generator Action Java version by National High Magnetic Field Laboratory.