About
Monte Carlo methods are often useful for solving problems in physics and mathematics, which cannot be solved by analytical means.
The goal of this virtual-lab is to obtain an approximated value of PI, using a Monte Carlo method. Next, we describe briefly how this method is used to estimate PI.
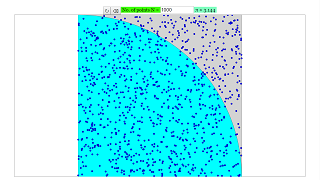
Imagine that we are throwing a dart over a square surface of side 1 m. There is a circle of radius 1 m. inscribed in the square. Assuming that the probability is uniformly distributed, the probability of hitting inside the circle is equal to PI/4. Dividing the number of hits by the number of throws, it is obtained an estimation of PI. We will obtain a better approximation by increasing the number of throws.
This virtual-lab allows the user to select the number of throws, with a maximum of 10000 throws.
Dpto. de Informática y Automática
E.T.S. de Ingeniería Informática, UNED
Juan del Rosal 16, 28040 Madrid, Spain
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits

Carla Martn; Tan Wei Chiong; Loo Kang Wee
end faq
Sample Learning Goals
[text]
For Teachers
Before, we had a simulation on the calculation of π using Archimedes' algorithm. This simulation shows yet another method that can be used to approximate the value of π.
The Monte Carlo method is done by taking a unit square (a square of length 1) and inscribing a quadrant inside. A arbitrary number of points is then randomly scattered in the square. Since the area of the square is 1 and the area of the inscribed quadrant is π/4, the ratio of the number of points that land in the quadrant to the total number of points becomes an estimate of π/4, which is then multiplied by 4 to estimate π.
This method is used widely in mathematics and physics when a problem cannot be solved analytically.
The number of points can be set up to 50000 points. Hit the randomize button to randomize the placement of the points.
Research
[text]
Video
[text]
Version:
- http://weelookang.blogspot.com/2018/05/monte-carlo-pi-calculation-javascript.html
- http://www.euclides.dia.uned.es/simulab-pfp/curso_online/cap7_caseStudies/sec_MonteCarloPI.htm by Alfonso Urquia and Carla Martin-Villalba
Other Resources
[text]
end faq
Testimonials (0)
There are no testimonials available for viewing. Login to deploy the article and be the first to submit your review!
You have to login first to see this stats.