About
7.1 Newton’s Law of Gravitation
Gravitation is a natural phenomenon by which physical bodies attract each other due to their masses. This force occurs whenever masses are present and the two bodies need not to be in contact with each other. It is however the weakest of the fundamental forces of nature.
In 1687, Sir Isaac Newton concluded that this non-contact gravitational force must be as responsible for the falling of the apple from a tree as it is the cause for the rotation of the Moon about the Earth. Hence he published the Newton’s law of gravitation which states that:
“The mutual force of attraction between any two point masses is directly proportional to the product of their masses and inversely proportional to the square of the separation between their centres.”
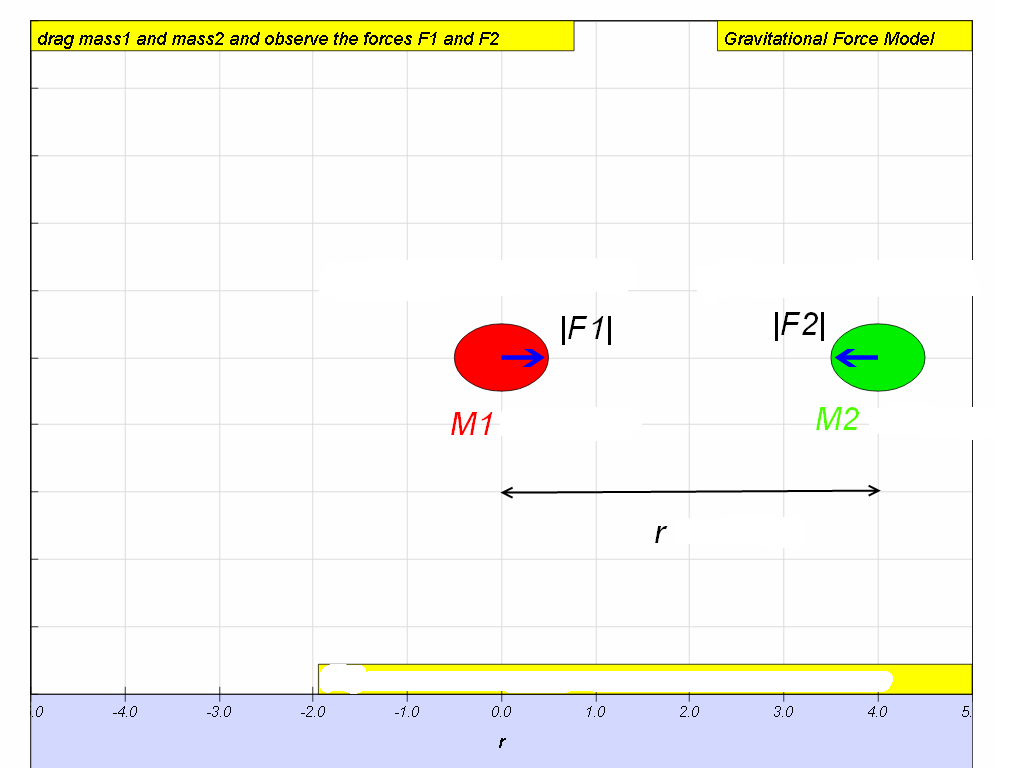
This means that if there are two point masses M and m and they are separated by distance r, the magnitude of the gravitational force attracting them to each other is where G, the constant of universal gravitation, is (will be given in data & formulae list during tests and examinations).
Note:
1. r is taken to be the centre to centre distance (i.e. centre of particle to centre of particle). Do not take r to be the radius of orbit!
2. This formula is an example of the inverse square law.
7.1.1 Inquiry:
What can you conclude about the two forces in the simulation below?Answer: Based on the evidences from the simulation triangulated with real life examples, the mutual force of attraction between any two point masses is directly proportional to the product of their masses and inversely proportional to the square of the separation between their centres.
7.1.2 Model:
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits


![]()
 This email address is being protected from spambots. You need JavaScript enabled to view it.; Anne Cox; Wolfgang Christian; Francisco Esquembre
This email address is being protected from spambots. You need JavaScript enabled to view it.; Anne Cox; Wolfgang Christian; Francisco Esquembre
end faq
Testimonials (0)
There are no testimonials available for viewing. Login to deploy the article and be the first to submit your review!
You have to login first to see this stats.