About

7.3 Gravitational Potential Energy (symbol: U and units: J)

7.3.1 in Work, Energy & Power topic

In the topic of Work, Energy & Power, the calculation of gravitational potential energy (GPE) is determined using the expression, mgh, which assumes that the gravitational field strength g is roughly constant, but a more robust formula is required for varying field strength, say when sending rockets which travel into outer space from the surface of the Earth.

ΔU = ΔPE = mgh or mgΔh

where ΔPE or ΔU is the gravitational potential energy possessed by mass m measured from the reference height h₀ , g is the gravitational field strength created by source mass M.

h or Δh is the change in the height (h₁ - h₀ ) of the mass m.

7.3.2 more universal formula for Potential energy

This formula PE = mgh or mgΔh was appropriate when the magnitude of gravitational field strength, g of Earth was assumed to be constant (9.81 m s^-2) over this height. When the assumption of constant gravitational field strength is not valid, a more robust PE formula is given by the calculation of potential energy 

$U=-m\frac{GM}{r}$

where

U is the gravitational potential energy possessed by mass m measured from the reference position of infinity,

G is the gravitational constant, approximately 6.673×10⁻¹¹ N·(m/kg)²,

M is the source mass that sets up the gravitational field,

m is the test mass experiencing the gravitational field set up by M, and

r is the distance away from the centre of the gravitational field source mass M

$$

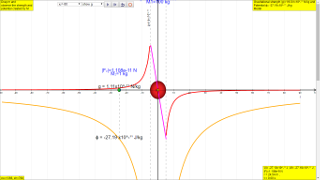
In this particular case, $U=-m\genfrac{}{}{0.1ex}{}{GM}{r}=-(1)\genfrac{}{}{0.1ex}{}{6.67x10^{-11}\left(100\right)}{100}=-6.67x10^{-11}J$

Calculate for the case when r = 50 m.

Similarly, $U=-m\genfrac{}{}{0.1ex}{}{GM}{r}=-(1)\genfrac{}{}{0.1ex}{}{6.67x10^{-11}\left(100\right)}{50}=-13.35x10^{-11}J$

7.3.3 Characteristics of Gravitational potential energy

equation is given by $U=-m\genfrac{}{}{0.1ex}{}{GM}{r}$

a scalar quantity (i.e. it has no direction only magnitude )

has only negative value due to the reference potential equal zero U = 0, position is defined at position r = infinity,  ∞, and gravity is attractive which means the lowest potential position is at the centre of the source mass M.

U = -infinity, at r = 0, lowest potential energy

U = 0, at r = infinity, highest potential energy   

Now, this leads to the need to define gravitational potential energy.

7.3.4 Definition of gravitational potential energy, U

The gravitational potential energy (U) of a mass m at a point (due to the gravitational field set up by mass M ) is defined as the work done by an external agent in bringing the mass from infinity to that point r distance away from source mass M.

To further understand the meaning of this definition, let's start with the definition for work done on external agent, where WD = WD _{by external agent}.

$WD=\underset{\infty }{\overset{r}{\int }}Fdx$
$$Substituting the formula for force F and working out the integration, it can be shown.

$WD=\underset{\infty }{\overset{r}{\int }}Fdr=\underset{\infty }{\overset{r}{\int }}\genfrac{}{}{0.1ex}{}{GMm}{r^2}$ $dr={\left[\frac{-GmM}{r}\right]}_r^{\infty }=[\genfrac{}{}{0.1ex}{}{-GmM}{r}-\genfrac{}{}{0.1ex}{}{-GmM}{\infty }]=-\genfrac{}{}{0.1ex}{}{GmM}{r}$

Notice the formula for this work done by external agent is equal to the U.

$WD=U=-\frac{GmM}{r}$

To understand this definition, we can use the simulation with some imagination.
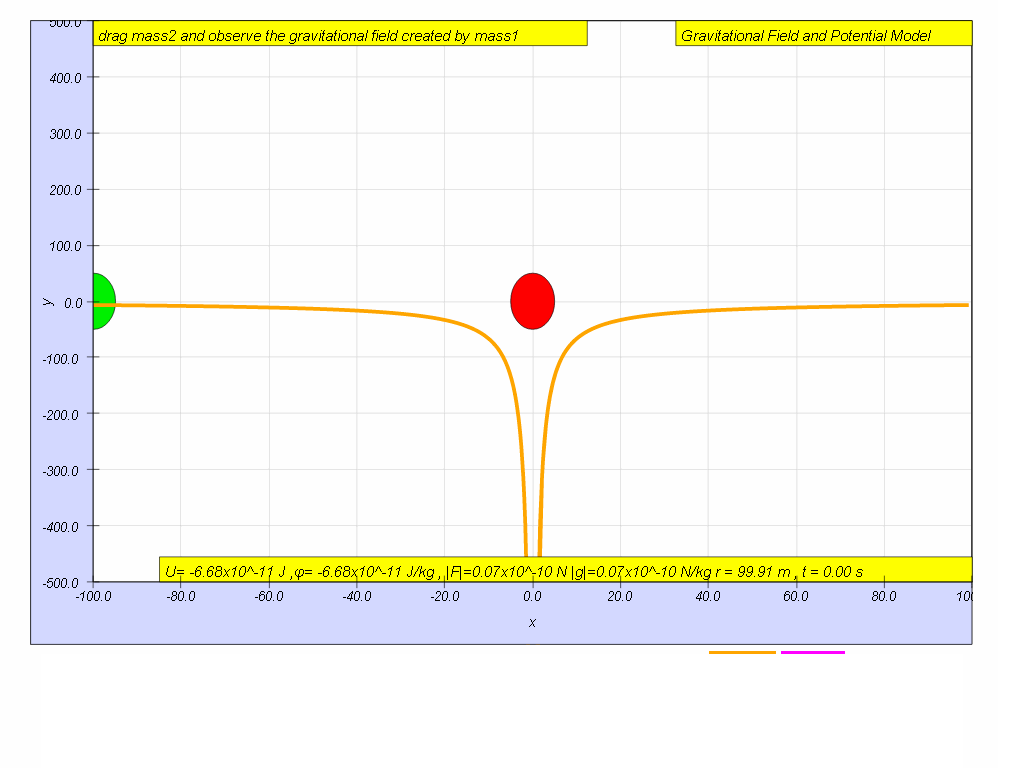
Imagine the test mass, m is at a distance r = ∞, U_∞ = 0 (the simulation does not allow r = ∞, but let's assume r = 100 is somewhat far enough)

Let imagine a force pointing towards infinity away from source mass M, acting on this test mass m, the potential energy of m at this point would be therefore the work done by this external force.

WD= U_final-U_initial=U_r-U_∞

which means that the work done by external force is equal to the gravitational potential energy (U_r) since U_∞ = 0.

7.3.5 Suggested activity

The intent of these activities is to allow students be like a student-scientists and collect their own data to form an understanding of potential energy.

The test mass (green) is at r = 100 m, observe and record the value for U _r=100 = -6.67 x10^-11 J

Click play and pause the model when r = 90 m, record the value of U _r=90 = ____________ J

Click play and pause the model when r = 80 m, record the value of U _r=80 = ____________ J

Click play and pause the model when r = 70 m, record the value of U _r=70 = ____________ J

Click play and pause the model when r = 60 m, record the value of U _r=60 = ____________ J

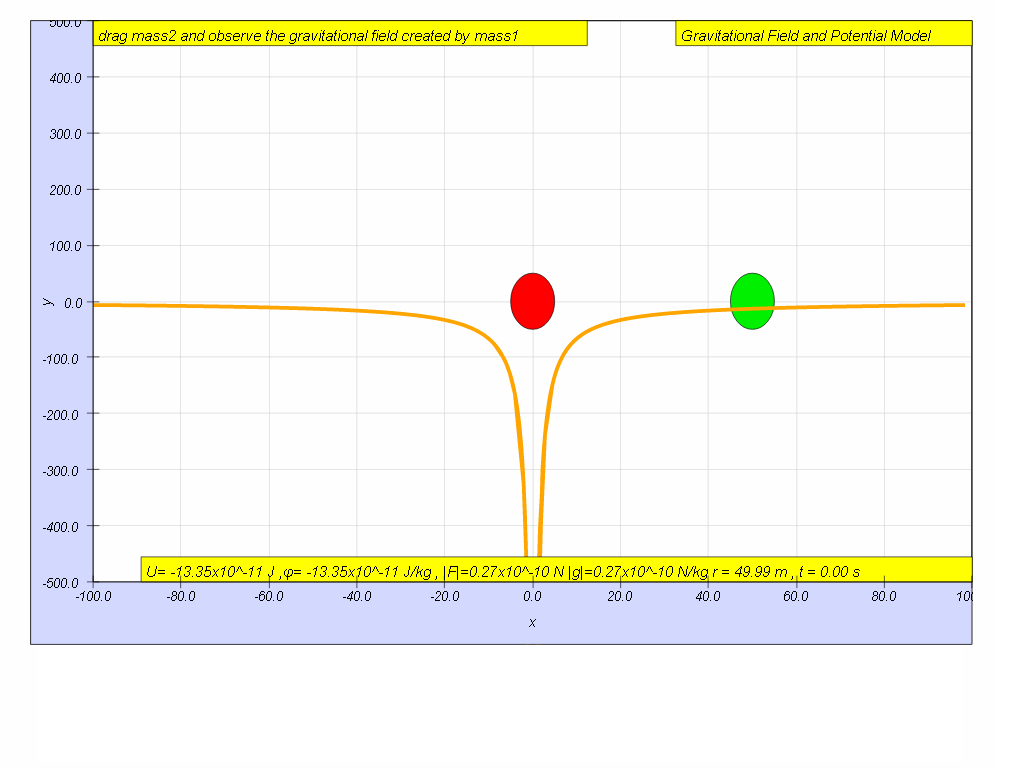
Click play and pause the model when r = 50 m, record the value of U _r=50 = ____________ J

Click play and pause the model when r = 40 m, record the value of U _r=40 = ____________ J

Click play and pause the model when r = 30 m, record the value of U _r=30 = ____________ J

Click play and pause the model when r = 20 m, record the value of U _r=20 = ____________ J

Calculate the change in U from r = 100 to r = 50.

Answer is about $\mathrm{\Delta U}=-[\genfrac{}{}{0.1ex}{}{6.67x10^{-11}\left(1\right)\left(100\right)}{50}-\genfrac{}{}{0.1ex}{}{6.67x10^{-11}\left(1\right)\left(100\right)}{100}]=-6.67x10^{-9}J$

Check the "your model" checkbox and a teal color line appear. For example if the model is , $U=-\genfrac{}{}{0.1ex}{}{GmM}{r}$, key in -6.67*1*100/abs(r) and observe the closeness of fit of the orange color line (data collected) versus the teal color line (model proposed).

Suggest with reason why you think the model -6.67*1*100/abs(r) is accurate.

Note that the model already has a multiple of x10^-11 so there is no need to key it.

7.3.6 Model:

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/57

 

Translations

Code	Language		Translator	Run

Software Requirements

	Android	iOS	Windows	MacOS
with best with	Chrome	Chrome	Chrome	Chrome
support full-screen?	Yes. Chrome/Opera No. Firefox/ Samsung Internet	Not yet	Yes	Yes
cannot work on	some mobile browser that don't understand JavaScript such as.....		cannot work on Internet Explorer 9 and below

 

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.; Anne Cox; Wolfgang Christian; Francisco Esquembre

end faq