About

7.3.8 Relationship between F and U; between g and ϕ

To understand how g is related to ϕ:

1. Similarly, compare $g=-\genfrac{}{}{0.1ex}{}{GM}{r^2}$ and $\text{ϕ}=-\frac{\text{GM}}{r}$ in the above table.
2. If we differentiate $\text{ϕ}=-\frac{\text{GM}}{r}$    with respect to r, we will get  $\genfrac{}{}{0.1ex}{}{d\varphi }{dr}=-\genfrac{}{}{0.1ex}{}{GM}{(-r^2)}$, which has the same expression as g.
3. Hence, mathematically $\genfrac{}{}{0.1ex}{}{d\varphi }{dr}=\genfrac{}{}{0.1ex}{}{GM}{r^2}=-g$
4. To understand the meaning of $g=-\genfrac{}{}{0.1ex}{}{d\varphi }{dr}$ observe the two graphs carefully, on the right side where r is positive, the gradient of ϕ vs r graph is positive but the value of g will be negative. And on the left side where r is negative, the gradient of ϕ vs r graph is negative but the value of g is positive. Thus, $g=-\genfrac{}{}{0.1ex}{}{d\varphi }{dr}$

Similarly, it can be concluded that by multiplying both sides by test mass m.

$mg=-\genfrac{}{}{0.1ex}{}{dm\varphi }{dr}$
thus $F=-\genfrac{}{}{0.1ex}{}{dm\varphi }{dr}$

7.3.8.1 Activity To do

ICT inquiry worksheet 1 (E), as well as the "G field and potential" EJS here. The HTML5 version is below, the Java worksheet customization to HTML5 is work in progress.

7.3.8.2 Summary

symbol	$g=-\genfrac{}{}{0.1ex}{}{GM}{r^2}$	$\text{ϕ}=-\frac{\text{GM}}{r}$
name	Field strength	Potential
units	N kg-1 or m s-2	J kg-1
meaning	Gravitational force per unit mass	Gravitational potential energy per unit mass
quantity	vector	scalar
equation	$\mathrm{|g|}=\genfrac{}{}{0.1ex}{}{GM}{r^2}$ towards the centre of the source mass	$\text{ϕ}=-\frac{\text{GM}}{r}$
relationship to mass	Force, $F=\frac{G{M}_1{M}_2}{r^2}$ = mg	Potential energy, $U=-m\genfrac{}{}{0.1ex}{}{GM}{r}$ = mϕ
graph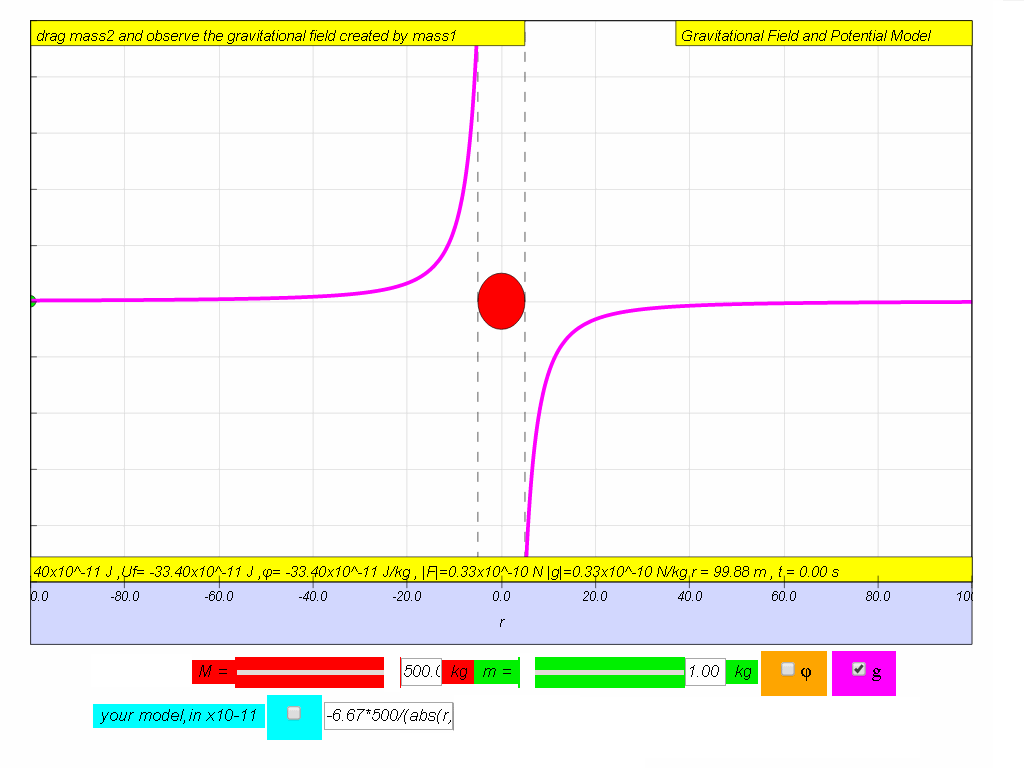
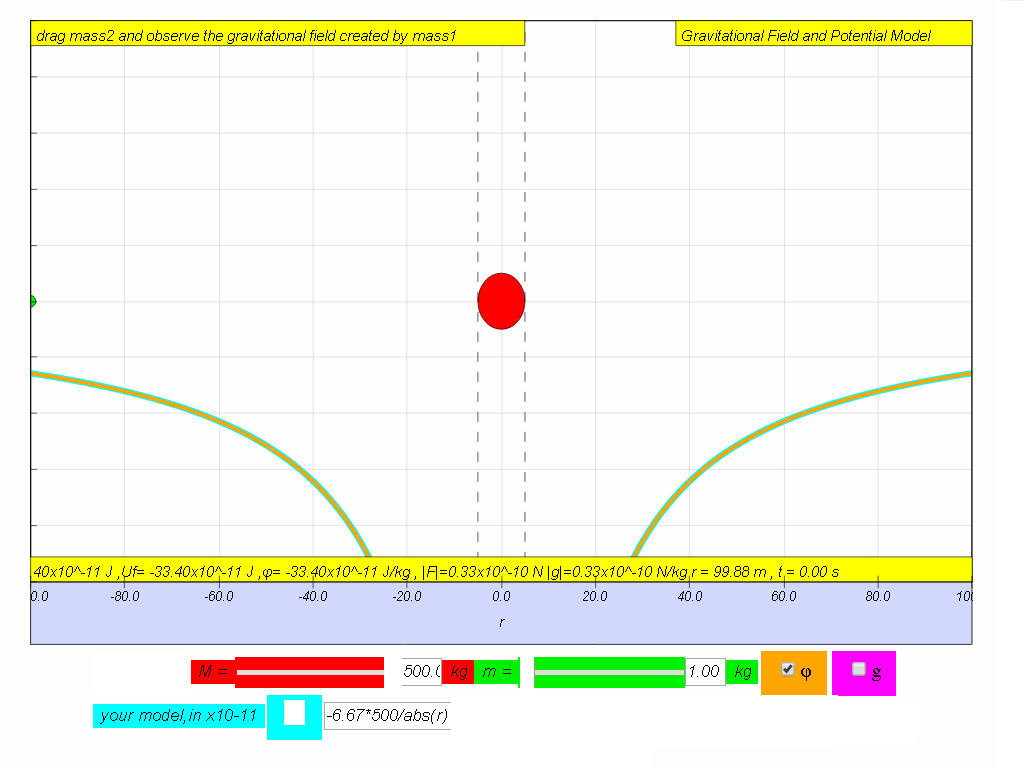computer model if M = 500.	-6.67*500/(abs(r)*r)	-6.67*500/abs(r)
relationship between g and ϕ	$g=-\genfrac{}{}{0.1ex}{}{d\varphi }{dr}$
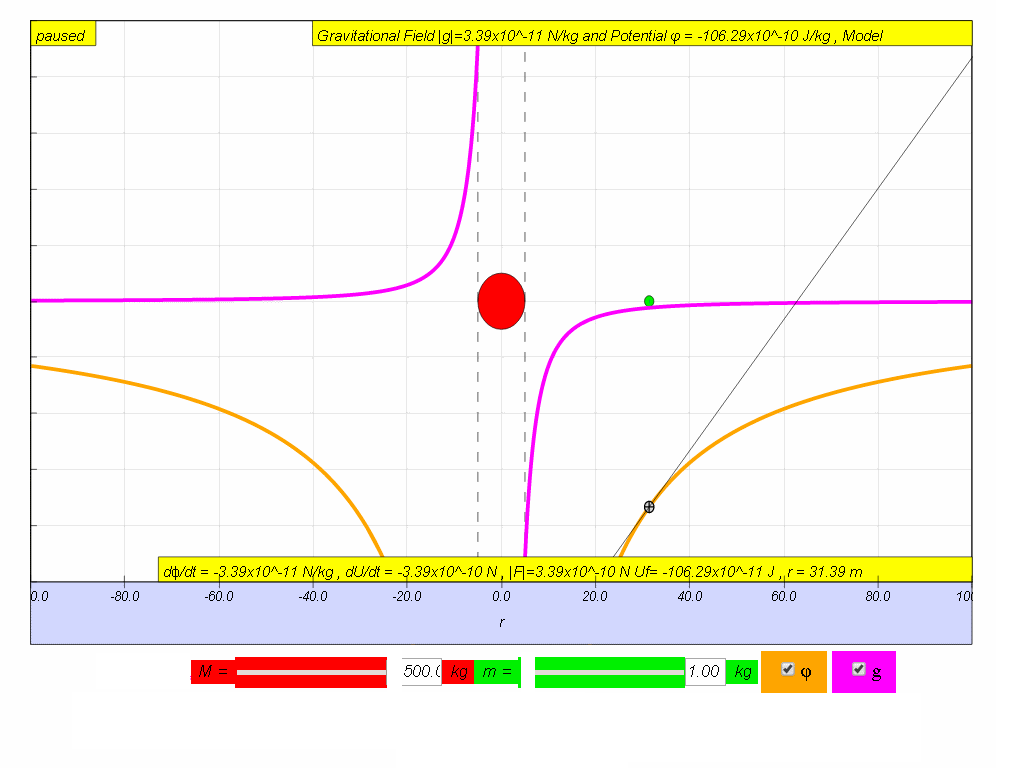relationship between F and U	$F=-\genfrac{}{}{0.1ex}{}{dU}{dr}$

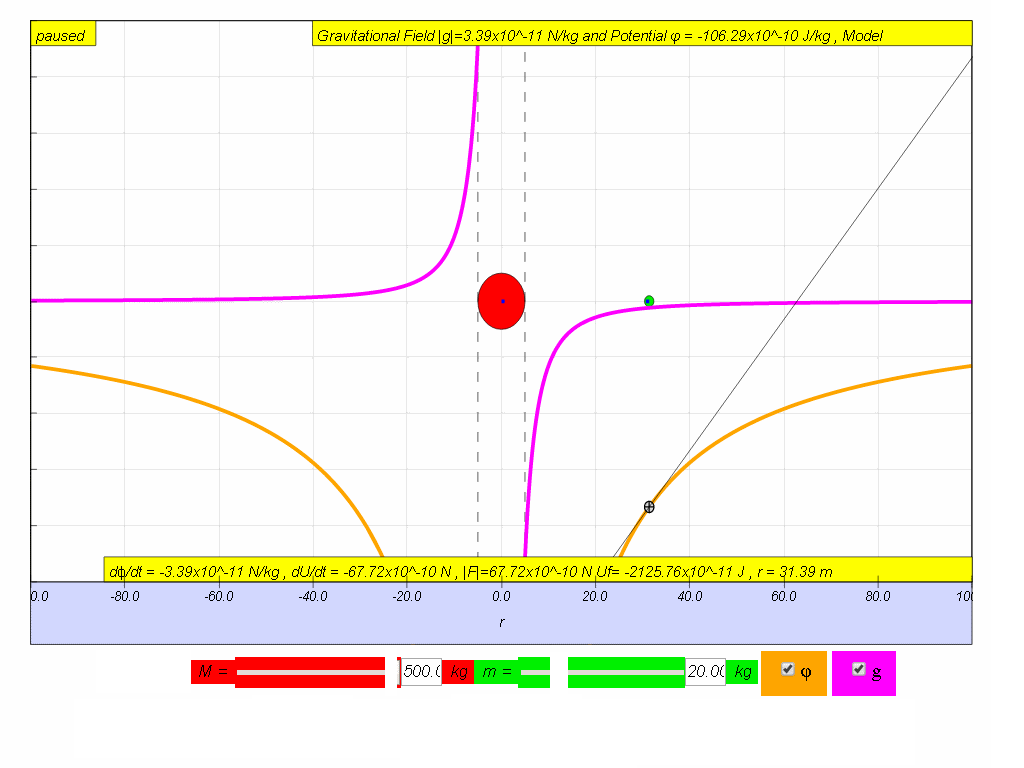7.3.8.3 Model

1. Run Sim
2. http://iwant2study.org/ospsg/index.php//59

 

Translations

Code	Language		Translator	Run

Software Requirements

	Android	iOS	Windows	MacOS
with best with	Chrome	Chrome	Chrome	Chrome
support full-screen?	Yes. Chrome/Opera No. Firefox/ Samsung Internet	Not yet	Yes	Yes
cannot work on	some mobile browser that don't understand JavaScript such as.....		cannot work on Internet Explorer 9 and below

 

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.; Anne Cox; Wolfgang Christian; Francisco Esquembre

end faq