About

1.2.7 Example

A body moves in a simple harmonic motion and the following graph gives the variation of its displacement x with time t.
 


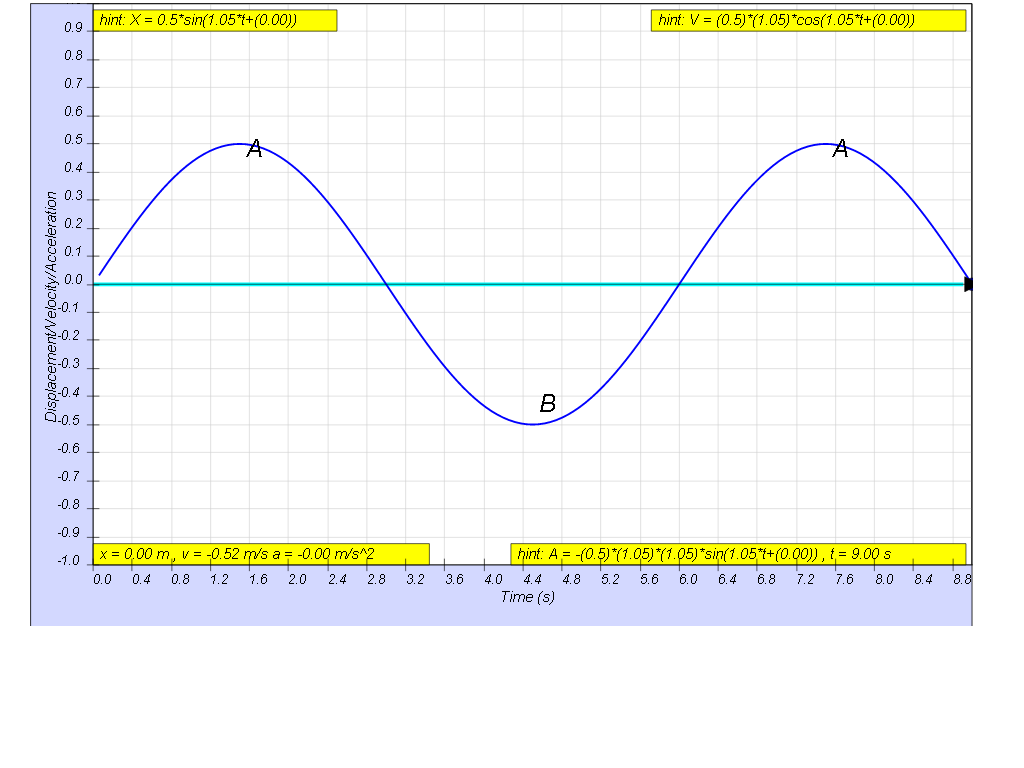
a)    Write an equation to represent the given simple harmonic motion.
b)    Find the time duration in the first cycle when the body is located above a displacement of 0.25 m.

[ x = x_o sin (1.05 t) , Δt = 1.9 s ]

The hint can be found in the model

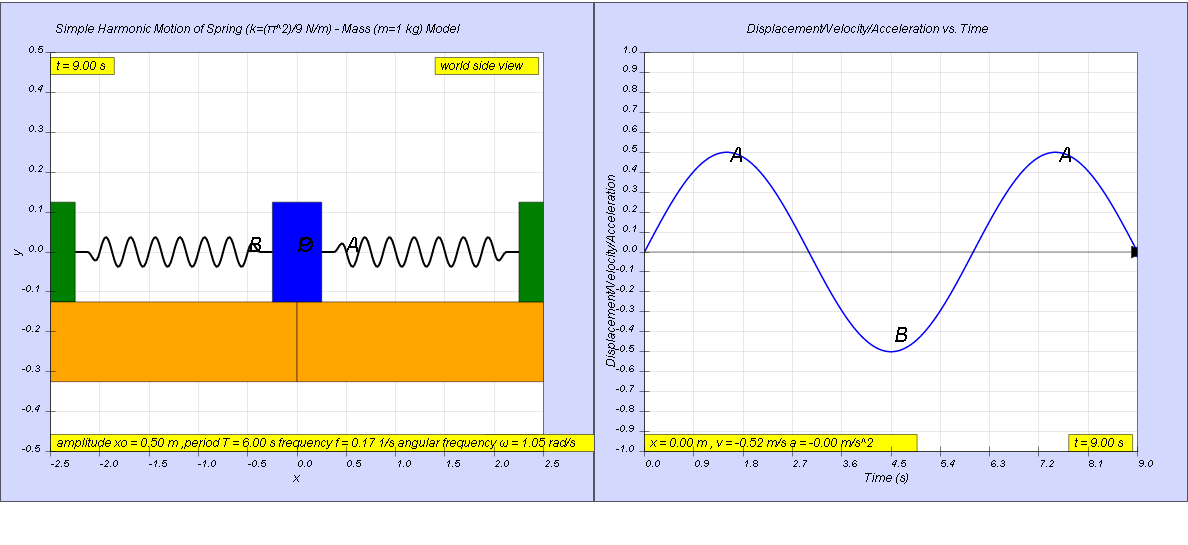
1.2.7.1 Solution:

a) x0 = 0.5 m

$\mathrm{since\; \omega }=\genfrac{}{}{0.1ex}{}{2\pi }{T}$ $\mathrm{,\; \omega }=\genfrac{}{}{0.1ex}{}{2\pi }{6.0}$$\mathrm{}$

ω = 1.05
x = x0sin(ω t) = 0.5 sin(1.05t)

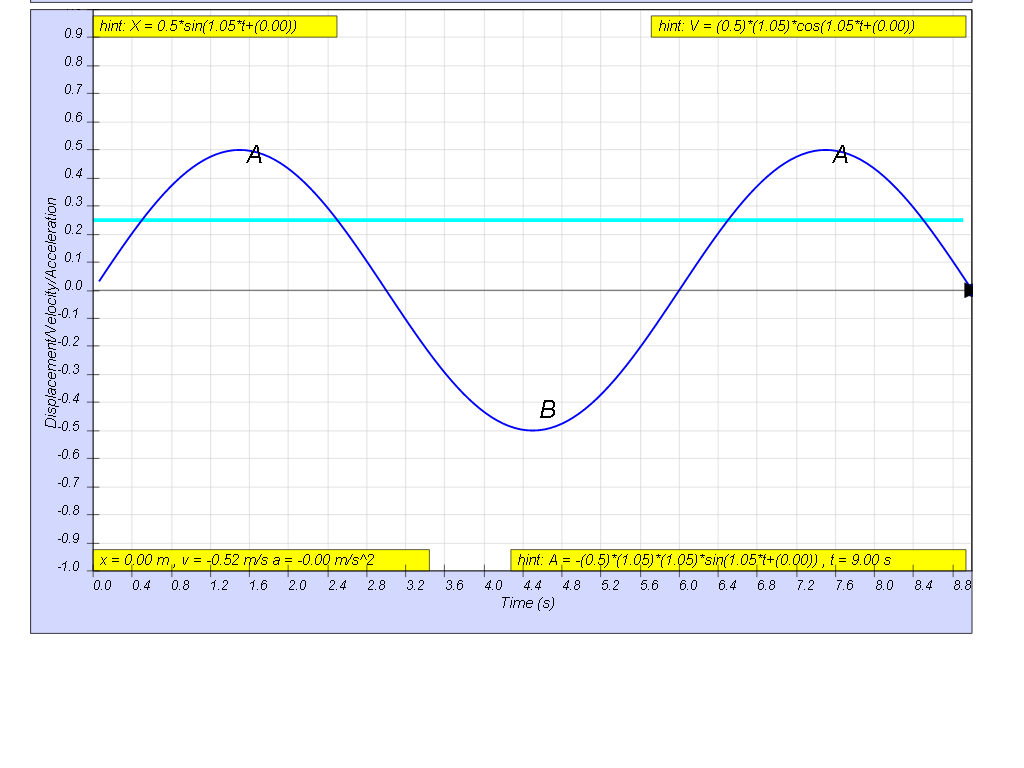
b) At x = 0.25 m,

substituting back into the equation,

0.25 = 0.5 sin(1.05t)

$\mathrm{}$solving for t gives

0.5 = sin(1.05t)

$$
solving of the ranging of time, t

1.05t = 0.524 and π - 0.524

t₁ = 0.5 , t₂ = 2.4 s

looking at the graphical form of the solution of the 2 times, t₁ and t₂.

giving the range to be t₂ - t₁ = 2.4 - 1.5 = 1.9 s

1.2.7.2 Model:

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/76

 

Translations

Code	Language		Translator	Run

Software Requirements

	Android	iOS	Windows	MacOS
with best with	Chrome	Chrome	Chrome	Chrome
support full-screen?	Yes. Chrome/Opera No. Firefox/ Samsung Internet	Not yet	Yes	Yes
cannot work on	some mobile browser that don't understand JavaScript such as.....		cannot work on Internet Explorer 9 and below

 

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.

end faq