About
1.1.3.2.3 Understanding Phase Difference through Uniform Circular Motion
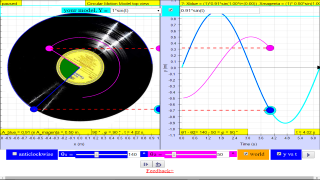
Simple harmonic motion can in some cases be considered to be the one-dimensional projection of uniform
circular motion. If an object moves with angular speed ω around a circle of radius A centered at the origin of the x−y plane, then its motion along each coordinate is simple harmonic motion with amplitude A and angular frequency ω.
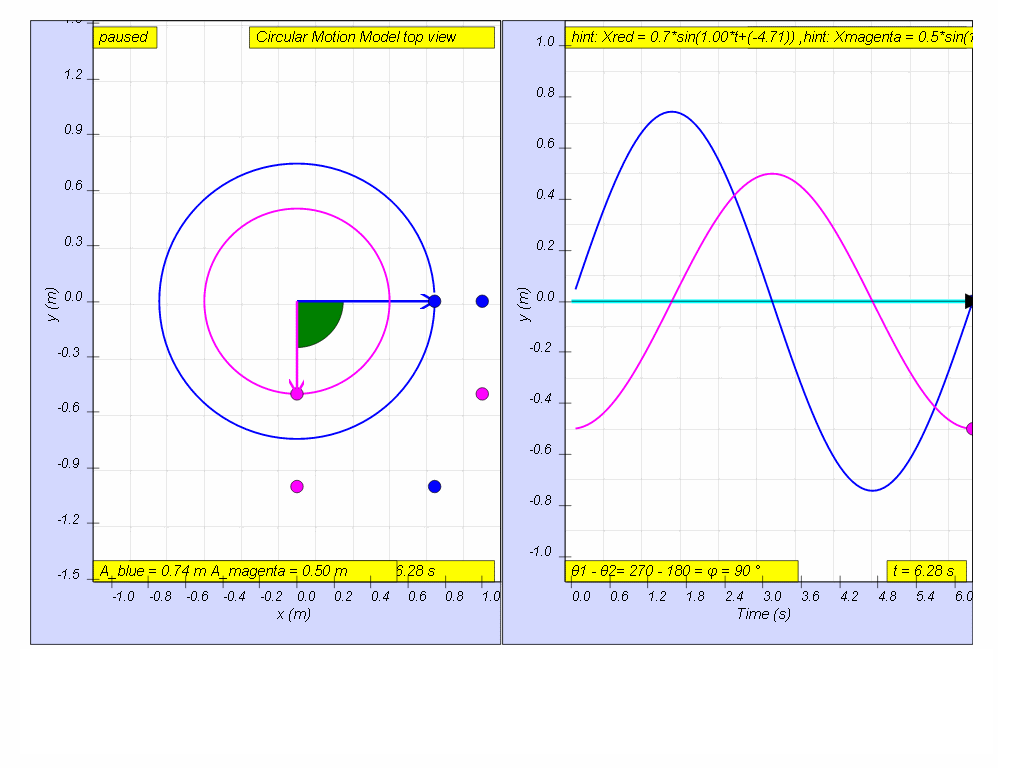
Q1: given that, a circular motion can be described by x = A cos(ω t) and y A sin(ω t) what is the y-component model-equation that can describe the motion of a uniform circular motion?
A1: y = Asin (ωt)
Q2: When the x-component of the circular motion is modelled by x = A cos(ω t) and y A sin(ω t) suggest an model-equation for y.
A2: y = Acos (ωt) for top position or y = - Acos (ωt) for bottom position
Q3: Explain why are the models for both x and y projection of a uniform circular motion, a simple harmonic motion?
A3: both x = A cos(ω t) and y A sin(ω t) each follow the defining relationship for SHM as ordinary differential equations of and respectively.
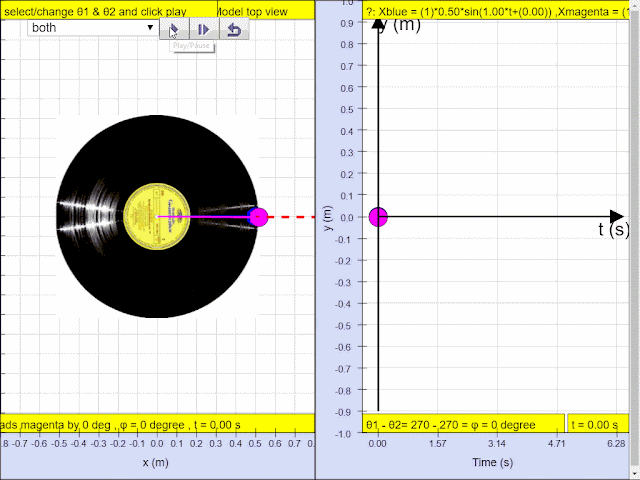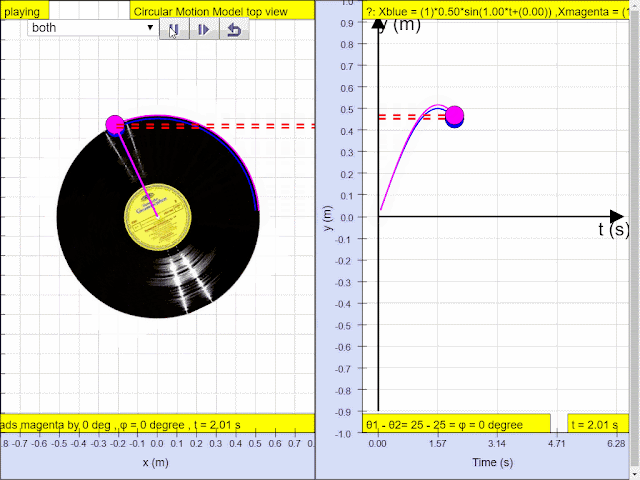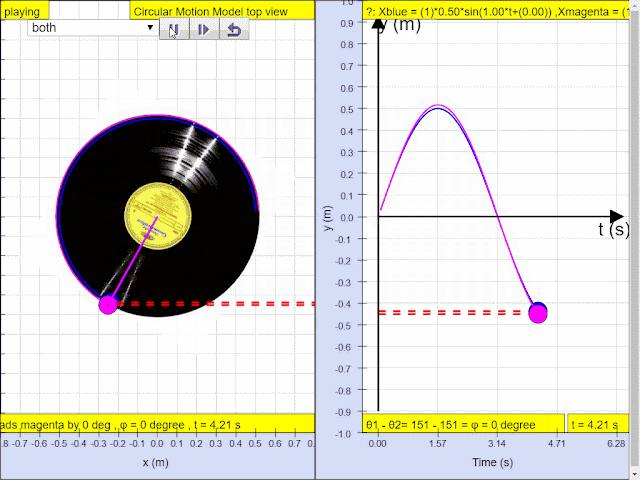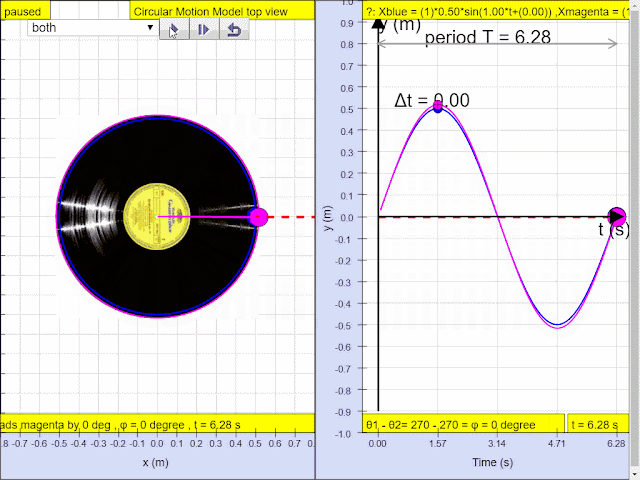
Q4: In, the diagram above, what is the phase difference between blue and magenta color y direction motion?
A4: the phase difference is 90 degrees, or more precisely blue lead red by 90 degrees angle.1.1.3.2.3.1 YouTube:
http://youtu.be/0IaKcqRw_Ts This video shows how a pendulum's oscillations and the shadow of rotating object are related. This could be used to demonstrate that the projection of a circular motion is actually a simple harmonic motion.
1.1.3.2.3.2 Run Model:
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits

 This email address is being protected from spambots. You need JavaScript enabled to view it.; Fu-Kwun Hwang
This email address is being protected from spambots. You need JavaScript enabled to view it.; Fu-Kwun Hwang
end faq
What is in Phase?
 |
Video
Version:
Other Resources
[text]
end faq
Testimonials (0)
There are no testimonials available for viewing. Login to deploy the article and be the first to submit your review!
You have to login first to see this stats.