About

Subject Area	Waves & Optics
Levels	First Year and Beyond the First Year
Available Implementation	Python
Learning Objectives	Students who complete this set of exercises will be able to predict and visually represent the irradiance distribution at a screen generated by a point light source and an aperture (Exercise 1); predict and visually represent the irradiance distribution at a screen generated by multiple point light sources and an aperture (Exercise 2); predict and visually represent the irradiance distribution at a screen generated by multiple point light sources and a complex aperture (Exercise 3); predict and visually represent the irradiance distribution at a screen generated by a two-dimensional array of point light sources and an aperture (Exercise 4);, and predict and visually represent the irradiance distribution at a screen generated by a two-dimensional array of point light sources and an opaque barrier (Exercise 5).
Time to Complete	120 min

EXERCISE 1: IRRADIANCE AT A SCREEN DUE TO A POINT SOURCE

We imagine that a point source of light at Ps=(xs,ys,zs)$P_{s}style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">=style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">(style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">x_{s}style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">,style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">y_{s}style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">,style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">z_{s}style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">)style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">$style="padding-top: 0px; padding-right: 0px; padding-bottom: 0px; padding-left: 0px; border-top-style: none; border-top-width: 0px; border-right-style: none; border-right-width: 0px; border-bottom-style: none; border-bottom-width: 0px; border-left-style: none; border-left-width: 0px; display: inline; margin-top: 0px; margin-right: 0px; margin-bottom: 0px; margin-left: 0px; line-height: normal"> illuminates an aperture in an opaque barrier located at z=0$zstyle="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">=style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">0style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">$style="padding-top: 0px; padding-right: 0px; padding-bottom: 0px; padding-left: 0px; border-top-style: none; border-top-width: 0px; border-right-style: none; border-right-width: 0px; border-bottom-style: none; border-bottom-width: 0px; border-left-style: none; border-left-width: 0px; display: inline; margin-top: 0px; margin-right: 0px; margin-bottom: 0px; margin-left: 0px; line-height: normal"> as shown below.

The irradiance of the light appearing at point P=(x,y,z)$Pstyle="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">=style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">(style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">xstyle="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">,style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">ystyle="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">,style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">zstyle="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">)style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">$style="padding-top: 0px; padding-right: 0px; padding-bottom: 0px; padding-left: 0px; border-top-style: none; border-top-width: 0px; border-right-style: none; border-right-width: 0px; border-bottom-style: none; border-bottom-width: 0px; border-left-style: none; border-left-width: 0px; display: inline; margin-top: 0px; margin-right: 0px; margin-bottom: 0px; margin-left: 0px; line-height: normal"> on the viewing screen located at z=zsc$zstyle="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">=style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">z_{sstyle="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">cstyle="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">}style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">$style="padding-top: 0px; padding-right: 0px; padding-bottom: 0px; padding-left: 0px; border-top-style: none; border-top-width: 0px; border-right-style: none; border-right-width: 0px; border-bottom-style: none; border-bottom-width: 0px; border-left-style: none; border-left-width: 0px; display: inline; margin-top: 0px; margin-right: 0px; margin-bottom: 0px; margin-left: 0px; line-height: normal"> is then given by

where A$Astyle="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">$style="padding-top: 0px; padding-right: 0px; padding-bottom: 0px; padding-left: 0px; border-top-style: none; border-top-width: 0px; border-right-style: none; border-right-width: 0px; border-bottom-style: none; border-bottom-width: 0px; border-left-style: none; border-left-width: 0px; display: inline; margin-top: 0px; margin-right: 0px; margin-bottom: 0px; margin-left: 0px; line-height: normal"> is a constant, r$rstyle="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">$style="padding-top: 0px; padding-right: 0px; padding-bottom: 0px; padding-left: 0px; border-top-style: none; border-top-width: 0px; border-right-style: none; border-right-width: 0px; border-bottom-style: none; border-bottom-width: 0px; border-left-style: none; border-left-width: 0px; display: inline; margin-top: 0px; margin-right: 0px; margin-bottom: 0px; margin-left: 0px; line-height: normal"> is the distance from PS$P_{S}style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">$style="padding-top: 0px; padding-right: 0px; padding-bottom: 0px; padding-left: 0px; border-top-style: none; border-top-width: 0px; border-right-style: none; border-right-width: 0px; border-bottom-style: none; border-bottom-width: 0px; border-left-style: none; border-left-width: 0px; display: inline; margin-top: 0px; margin-right: 0px; margin-bottom: 0px; margin-left: 0px; line-height: normal"> (the source) to P$Pstyle="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">$style="padding-top: 0px; padding-right: 0px; padding-bottom: 0px; padding-left: 0px; border-top-style: none; border-top-width: 0px; border-right-style: none; border-right-width: 0px; border-bottom-style: none; border-bottom-width: 0px; border-left-style: none; border-left-width: 0px; display: inline; margin-top: 0px; margin-right: 0px; margin-bottom: 0px; margin-left: 0px; line-height: normal"> (the screen point), and T(x,y)$Tstyle="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">(style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">xstyle="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">,style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">ystyle="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">)style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">$style="padding-top: 0px; padding-right: 0px; padding-bottom: 0px; padding-left: 0px; border-top-style: none; border-top-width: 0px; border-right-style: none; border-right-width: 0px; border-bottom-style: none; border-bottom-width: 0px; border-left-style: none; border-left-width: 0px; display: inline; margin-top: 0px; margin-right: 0px; margin-bottom: 0px; margin-left: 0px; line-height: normal"> is a function we call the ‘transparency function’. If the line from the source at Ps$P_{s}style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">$style="padding-top: 0px; padding-right: 0px; padding-bottom: 0px; padding-left: 0px; border-top-style: none; border-top-width: 0px; border-right-style: none; border-right-width: 0px; border-bottom-style: none; border-bottom-width: 0px; border-left-style: none; border-left-width: 0px; display: inline; margin-top: 0px; margin-right: 0px; margin-bottom: 0px; margin-left: 0px; line-height: normal"> to the screen point P$Pstyle="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">$style="padding-top: 0px; padding-right: 0px; padding-bottom: 0px; padding-left: 0px; border-top-style: none; border-top-width: 0px; border-right-style: none; border-right-width: 0px; border-bottom-style: none; border-bottom-width: 0px; border-left-style: none; border-left-width: 0px; display: inline; margin-top: 0px; margin-right: 0px; margin-bottom: 0px; margin-left: 0px; line-height: normal"> passes through the aperture, then T(x,y)=1$Tstyle="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">(style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">xstyle="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">,style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">ystyle="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">)style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">=style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">1style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">$style="padding-top: 0px; padding-right: 0px; padding-bottom: 0px; padding-left: 0px; border-top-style: none; border-top-width: 0px; border-right-style: none; border-right-width: 0px; border-bottom-style: none; border-bottom-width: 0px; border-left-style: none; border-left-width: 0px; display: inline; margin-top: 0px; margin-right: 0px; margin-bottom: 0px; margin-left: 0px; line-height: normal">; otherwise, T(x,y)=0$Tstyle="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">(style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">xstyle="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">,style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">ystyle="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">)style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">=style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">0style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">$style="padding-top: 0px; padding-right: 0px; padding-bottom: 0px; padding-left: 0px; border-top-style: none; border-top-width: 0px; border-right-style: none; border-right-width: 0px; border-bottom-style: none; border-bottom-width: 0px; border-left-style: none; border-left-width: 0px; display: inline; margin-top: 0px; margin-right: 0px; margin-bottom: 0px; margin-left: 0px; line-height: normal">. In the case where the aperture is a rectangle of width w$wstyle="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">$style="padding-top: 0px; padding-right: 0px; padding-bottom: 0px; padding-left: 0px; border-top-style: none; border-top-width: 0px; border-right-style: none; border-right-width: 0px; border-bottom-style: none; border-bottom-width: 0px; border-left-style: none; border-left-width: 0px; display: inline; margin-top: 0px; margin-right: 0px; margin-bottom: 0px; margin-left: 0px; line-height: normal"> in the x$xstyle="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">$style="padding-top: 0px; padding-right: 0px; padding-bottom: 0px; padding-left: 0px; border-top-style: none; border-top-width: 0px; border-right-style: none; border-right-width: 0px; border-bottom-style: none; border-bottom-width: 0px; border-left-style: none; border-left-width: 0px; display: inline; margin-top: 0px; margin-right: 0px; margin-bottom: 0px; margin-left: 0px; line-height: normal">-direction and height h$hstyle="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">$style="padding-top: 0px; padding-right: 0px; padding-bottom: 0px; padding-left: 0px; border-top-style: none; border-top-width: 0px; border-right-style: none; border-right-width: 0px; border-bottom-style: none; border-bottom-width: 0px; border-left-style: none; border-left-width: 0px; display: inline; margin-top: 0px; margin-right: 0px; margin-bottom: 0px; margin-left: 0px; line-height: normal"> in the y$ystyle="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">$style="padding-top: 0px; padding-right: 0px; padding-bottom: 0px; padding-left: 0px; border-top-style: none; border-top-width: 0px; border-right-style: none; border-right-width: 0px; border-bottom-style: none; border-bottom-width: 0px; border-left-style: none; border-left-width: 0px; display: inline; margin-top: 0px; margin-right: 0px; margin-bottom: 0px; margin-left: 0px; line-height: normal">-direction, show that the value of the transparency function is given byAlt Figure

Compute the irradiance on an array of uniformly spaced screen points on the viewing screen for an aperture with w=4.0$wstyle="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">=style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">4.0style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">$style="padding-top: 0px; padding-right: 0px; padding-bottom: 0px; padding-left: 0px; border-top-style: none; border-top-width: 0px; border-right-style: none; border-right-width: 0px; border-bottom-style: none; border-bottom-width: 0px; border-left-style: none; border-left-width: 0px; display: inline; margin-top: 0px; margin-right: 0px; margin-bottom: 0px; margin-left: 0px; line-height: normal"> cm and h=3.0$hstyle="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">=style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">3.0style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">$style="padding-top: 0px; padding-right: 0px; padding-bottom: 0px; padding-left: 0px; border-top-style: none; border-top-width: 0px; border-right-style: none; border-right-width: 0px; border-bottom-style: none; border-bottom-width: 0px; border-left-style: none; border-left-width: 0px; display: inline; margin-top: 0px; margin-right: 0px; margin-bottom: 0px; margin-left: 0px; line-height: normal"> cm in the following cases:

xS$x_{S}style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">$style="padding-top: 0px; padding-right: 0px; padding-bottom: 0px; padding-left: 0px; border-top-style: none; border-top-width: 0px; border-right-style: none; border-right-width: 0px; border-bottom-style: none; border-bottom-width: 0px; border-left-style: none; border-left-width: 0px; display: inline; margin-top: 0px; margin-right: 0px; margin-bottom: 0px; margin-left: 0px; line-height: normal"> [cm]	yS$y_{S}style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">$style="padding-top: 0px; padding-right: 0px; padding-bottom: 0px; padding-left: 0px; border-top-style: none; border-top-width: 0px; border-right-style: none; border-right-width: 0px; border-bottom-style: none; border-bottom-width: 0px; border-left-style: none; border-left-width: 0px; display: inline; margin-top: 0px; margin-right: 0px; margin-bottom: 0px; margin-left: 0px; line-height: normal"> [cm]	zS$z_{S}style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">$style="padding-top: 0px; padding-right: 0px; padding-bottom: 0px; padding-left: 0px; border-top-style: none; border-top-width: 0px; border-right-style: none; border-right-width: 0px; border-bottom-style: none; border-bottom-width: 0px; border-left-style: none; border-left-width: 0px; display: inline; margin-top: 0px; margin-right: 0px; margin-bottom: 0px; margin-left: 0px; line-height: normal"> [cm]	zsc$z_{sstyle="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">cstyle="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">}style="padding-top:\; 0px;\; padding-right:\; 0px;\; padding-bottom:\; 0px;\; padding-left:\; 0px;\; border-top-style:\; none;\; border-top-width:\; 0px;\; border-right-style:\; none;\; border-right-width:\; 0px;\; border-bottom-style:\; none;\; border-bottom-width:\; 0px;\; border-left-style:\; none;\; border-left-width:\; 0px;\; display:\; inline;\; margin-top:\; 0px;\; margin-right:\; 0px;\; margin-bottom:\; 0px;\; margin-left:\; 0px;\; line-height:\; normal">$style="padding-top: 0px; padding-right: 0px; padding-bottom: 0px; padding-left: 0px; border-top-style: none; border-top-width: 0px; border-right-style: none; border-right-width: 0px; border-bottom-style: none; border-bottom-width: 0px; border-left-style: none; border-left-width: 0px; display: inline; margin-top: 0px; margin-right: 0px; margin-bottom: 0px; margin-left: 0px; line-height: normal"> [cm]
0.0	0.0	-20.0	40.0
5.0	0.0	-20.0	40.0
0.0	5.0	-20.0	40.0
0.0	0.0	-10.0	40.0
0.0	0.0	-40.0	40.0
0.0	0.0	-20.0	60.0
0.0	0.0	-20.0	20.0

Does the computed light pattern change as you expect when you change the source and screen locations? Are the edges of the light pattern sharp or fuzzy? (How do you define “sharp” and “fuzzy”?) Why?

#

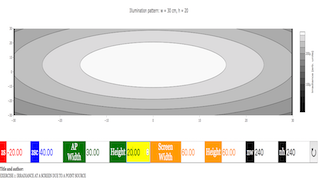
# Shadows_Exercise_1.py

#

# A point source is located a specified distance from

# a rectangular aperture that is centered on the origin.

# A screen is located a specified distance from

# the aperture.

#

# This file will generate a filled contour plot of

# the irradiance of the light reaching the screen

# versus lateral coordinates (x,y)

#

# Written by:

#

# Ernest R. Behringer

# Department of Physics and Astronomy

# Eastern Michigan University

# Ypsilanti, MI 48197

# (734) 487-8799

# This email address is being protected from spambots. You need JavaScript enabled to view it.

#

# 20160112-13 original code by ERB

# 20160609 clean up by ERB

#

# import the commands needed to make the plot

from pylab import xlabel,ylabel,show,contourf,axis,colorbar,figure,title,xlim,ylim

from matplotlib import cm

# import the command needed to make a 1D array

from numpy import meshgrid,absolute,where,zeros,linspace

# inputs

zs = -20.0 # distance between the source and aperture [cm]

zsc = 40.0 # distance between the screen and aperture [cm]

rso = [5.0,0.0] # (x,y) location of the source [cm,cm]

ap_width = 4.0 # aperture width [cm]

ap_height = 3.0 # aperture height [cm]

screen_width = 60.0 # screen width [cm]

screen_height = 60.0 # wcreen height [cm]

nw = 240 # Number of screen width intervals

nh = 240 # Number of screen height intervals

# initialize needed arrays to zero

screen_x = zeros((nw+1,nh+1)) # x coordinates of screen points

screen_y = zeros((nw+1,nh+1)) # y coordinates of screen points

rsq = zeros((nw+1,nh+1)) # source-to-screen point distance, squared

x0 = zeros((nw+1,nh+1)) # x coordinates of ray intercepts at aperture plane

y0 = zeros((nw+1,nh+1)) # y coordinates of ray intercepts at aperture plane

# initialize values

screen_xx = linspace(-0.5*screen_width,0.5*screen_width,nw+1)

screen_yy = linspace(-0.5*screen_height,0.5*screen_height,nh+1)

# create the meshgrid on which to evaluate the irradiance

screen_xx, screen_yy = meshgrid(screen_xx,screen_yy)

# Calculate grid increments

deltaw = screen_width/nw # grid increment, width [cm]

deltah = screen_height/nh # grid increment, height [cm]

# Define the array of screen x and screen y values

for i in range (0,nw+1):

for j in range (0,nh+1):

screen_x[i,j] = -0.5*screen_width + deltaw*i

screen_y[i,j] = -0.5*screen_height + deltah*j

# Calculate the intensity at each screen point

for i in range (0,nw+1):

for j in range (0,nh+1):

# First calculate the square of the distance from source to screen

rsq = (screen_x[i,j]-rso[0])**2 + (screen_y[i,j]-rso[1])**2 + (zsc - zs)**2

# Calculate x and y coordinates at the aperture

x0[i,j] = rso[0] + abs(zs)*(screen_x[i,j] - rso[0])/(zsc - zs)

y0[i,j] = rso[1] + abs(zs)*(screen_y[i,j] - rso[1])/(zsc - zs)

# Check if the coordinates fall within the aperture

maskx = where(absolute(x0) < 0.5*ap_width,1.0,0.0)

masky = where(absolute(y0) < 0.5*ap_height,1.0,0.0)

# Calculate the intensity

irradiance = maskx*masky/rsq

# make a filled contour plot of the period vs overlap and length ratios

figure()

contourf(screen_yy,screen_xx,irradiance,100,cmap=cm.bone)

axis('equal')

xlim(-0.5*screen_width,0.5*screen_width)

ylim(-0.5*screen_height,0.5*screen_height)

xlabel("\(x\) [cm]",size = 16)

ylabel("\(y\) [cm]",size = 16)

title('Illumination pattern: \(w = \)%s cm, \(h = \)%s'%(ap_width,ap_height),size = 16)

colorbar().set_label(label='Irradiance [arb. units]',size=16)

show()

 

Translations

Code	Language		Translator	Run

Software Requirements

	Android	iOS	Windows	MacOS
with best with	Chrome	Chrome	Chrome	Chrome
support full-screen?	Yes. Chrome/Opera No. Firefox/ Samsung Internet	Not yet	Yes	Yes
cannot work on	some mobile browser that don't understand JavaScript such as.....		cannot work on Internet Explorer 9 and below

 

Credits

Fremont Teng; Loo Kang Wee; based on codes by E. Behringer

end faq