Embed this model in a webpage:

<iframe width="100%" height="100%" src="https://iwant2study.org/lookangejss/06QuantumPhysics_20nuclear/ejss_model_decaychangeNwee/decaychangeNwee_Simulation.xhtml " frameborder="0"></iframe>

About

Designed by Fu-Kwun Hwang http://www.phy.ntnu.edu.tw/ntnujava/ http://weelookang.blogspot.sg/2015/12/ejss-radioactive-decay-model.html  

Translations

Code	Language		Translator	Run

Software Requirements

	Android	iOS	Windows	MacOS
with best with	Chrome	Chrome	Chrome	Chrome
support full-screen?	Yes. Chrome/Opera No. Firefox/ Samsung Internet	Not yet	Yes	Yes
cannot work on	some mobile browser that don't understand JavaScript such as.....		cannot work on Internet Explorer 9 and below

 

Credits

Fu-Kwun Hwang - Dept. of Physics, National Taiwan Normal Univ.; lookang

end faq

http://iwant2study.org/lookangejss/06QuantumPhysics_20nuclear/ejss_model_decaychangeNwee/decaychangeNwee_Simulation.xhtml

Theory

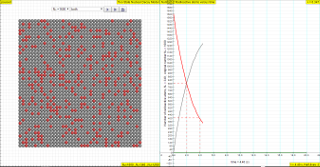
The law of radioactive decay predicts how the number of the not decayed nuclei of a given radioactive substance decreases in the course of time. The GREY circles of this simulation symbolize 100 (variable selectable up 400 or 1024) to  atomic nuclei of a radioactive substance whose half-life period (T_1/2) amounts to 0.1 to 3.0 seconds. The scientfic graph on the right, in number of radioactive atoms versus time, RED trail represents represents the Number of radioactive atoms, N₁ not yet decayed nuclei at a given time t, predicted by the following law:

N₁   =   N₀ e -(ln2/T^_1/2)) t

when you play with the show model option, show me N₁= N_o*exp(-ln(2)/T_1/2*t)

similarly it is possible to also predict the number of decayed atoms using the formula

N₂  =   N₀ -N₀ e -(ln2/T^_1/2)) t

when you play with the show model option, show me N2  = No-No*exp(-ln(2)/T_1/2*t)

in the option both2 when selected, can display the rate of radioactive atoms versus time,

dN = pN0 e -(ln2/T_^1/2)) t

when you play with the show model option, show me dN = p*N0*exp(-ln(2)/T_1/2*t)

the terms use are

N1 .... number of the not decayed nuclei

N₂ .... number of the decayed nuclei

N₀ ... number of the initially existing nuclei at time, t = 0
t .... time
T_1/2 ....  is the time taken for the activity of a given amount of a radioactive substance to decay to half of its initial value

 λ,  or sometimes also known as "lambda" the inverse of the mean lifetime, sometimes referred to as simply decay rate.

 p  is probability of decaying where 0 means no chance at all, 1 is 100% chance of decaying

Formula that related some of these terms are

T_1/2 = ln(2)/λ

 \( \lambda = \frac{p}{dt} \)

The Ordinary Differential equations used is

\( \frac{dN_{1}}{dt} =  - \lambda_{1}N_{1} \)

Versions

1. http://weelookang.blogspot.sg/2016/02/a-comparison-of-2-javascript-nuclear.html comparison of 2 HTML5 versions
2. http://weelookang.blogspot.sg/2015/12/ejss-radioactive-decay-model.html lookang's blogpost about this JavaScript version
3. http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=194.0 by Fu-Kwun Hwang original Java version
4. http://www.opensourcephysics.org/items/detail.cfm?ID=10576 by Wolfgang Christian similar Java version

Other Resources

1. http://www.opensourcephysics.org/items/detail.cfm?ID=13978&S=7 Two-State Nuclear Decay JS Model written by Wolfgang Christian
2. http://www.walter-fendt.de/html5/phen/lawdecay_en.htm by Walter fendt

end faq

You have to login first to see this stats.