About
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
| es | es | es |  |
|
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits

 Michael R. Gallis; lookang
Michael R. Gallis; lookang
end faq
Physics Explained Differential Absorption and Diagnostic X-Rays
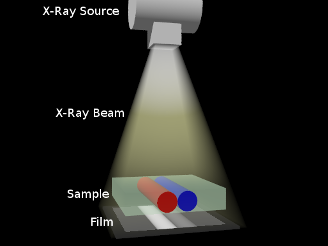
Differential Absorption and Diagnostic X-Rays
X-ray images are created when X-rays from a source penetrate an object and then expose a film. The difference in how different materials absorb the X-rays in the beam produces the contrast that generates the detail of the image.
For a typical medical diagnostic image, the X-ray interaction with matter is primarily through the Photoelectric effect and Compton scattering.
The strength of these two mechanisms depends upon the energy of the X-ray photons, the atomic number of the material as well as the density of the material.
This simulation provides a qualitative exploration of the difference of how X-rays interact with varying material properties and how this difference can produce contrast in the x-ray image.
Student Activities: Questions to explore:
The probability that an X-Ray photon will interact with the material depens upon the properties of the material as well as the properties of the photon. For diagnostic X-rays, the photon energies lie between a few keV and 150 keV. These X-rays interact with matter primarily through the Photoelectric Effect and Comptonb Scattering.
This applet simulates the interaction of X-rays 0f a particular energy going through slabs of material. For the purposes of comparison, two slabs are placed side by side, and a simulated X-Ray image is shown. Graphs are provided of the attenuation cofficients at different X-Ray photon energies. The attenuation coefficient is essentially the probability that the X-ray photon will interact with the material (withought taking into account the thickness of the sample of material). Graphs are also provided for the transmission of X-rays at different energies. The transmission graphs go from 0 (no X-Rays at that energy are transmitted) to 1 (all of the X-Rays at that energy are transmitted). The transmission graphs do include the effects of the thickness of the sample.
Experiment with different material settings. You can change the atomic number and the density of the two slabs separately. You can also change the thickness of the slides, but they will always have the same thickness. You can also control the photon energy1 and exposure (think of this as setting mAs). Mixtures of materials (such as bone, soft tissue and other materials) use an averaging process to determine an effective atomic number.
- How does increasing the atomic number (Z) affect the attenuation coefficient graph?
- How does increasing the atomic number affect the transmission graph?
- How does increasing the density (ρ) affect the attenuation coefficient graph?
- How does increasing the density affect the transmission graph?
Changing the photon energy just changes the energy for the simulated exposure, and is indicated by the markers on the graph.
- Verify that changing the photon energy does not change the graphs.
- Does changing the photon energy change the simulated film?
The exposure control is essentially an uncalibrated version of mAs for the radiation technologist.
- Does increasing or decreasing exposure affect any of the graphs?
- Does increasing or decreasing exposure affect the simulated film the way a similar increase in mAs would affect a real X-Ray image?
Use the preselected material properties for lung tissue for the left slab of material and soft tissue for the right slab of material. Make sure to set the other parameters to their defaults (Photon Energy = 50 keV, thickness = 1.0 cm, exposure = 1.0). The attenuation coefficient curve (in blue) for lung tissue is less than that for soft tissue (in red) at all X-ray photon energies. This means that the photons are more likely to interact with the material if they pass through soft tissue than if they were to pass through lung tissue.
- Which material will the X-Ray photons be more likely to pass through? Do the respective transmission curves show what you expect? Explain.
- With these two materials, vary the Photon Energy but leave the thickness set to 1 cm and the exposure set to 1. Is there an energy or range of energies that give a "best" contrast between the two sides in the simulated X-Ray film? Is there some feature of the transmission graphs that could explain this "best" contrast?
- Set the thickness to 10 cm. Can you predict what range of Photon Energy would give better contrast?
- Reset the thickness to 1 cm, and now select the left side material as bone and the right side material as Barium. Using the transmission graphs, make a prediction for a range of energies which will penetrate each slab.
1 Remember that real diagnostic X-Ray machines produce photons at a variety of efferent energies. The amount of photons at a particular energy is called the X-Ray spectrum and will depend upon kVp, tube current and the xray target material (usually Tungsten).
Description
The reduction of X-ray intensity due to absorbtion follows the following exponential decay:
I = I0 exp(-μt)
where I is the incident intensity, I0 is the transmitted intensity, μ is the absorption coefficient, and t is the thickness of the matterial. the mass absorption coefficient
μm = μ/ρ
is usually used in place of μ and a mass thickness
x=ρt
used in place of the physical thickness of the attenuating material.
Over the range of X-ray energies found in a typical diagnostic X-rays, μm is dominated by contributions from the phtoelectric effect (τm) and the Compton effect (σCm):
μm = τm+σCm
According to both reference 2 and 3, τm is proportional to the cube of atomic number Z and inversely proportional to the cube of the X-ray photon energy E. The behavior of σCm is less well defined. Both reference 2 and 3 note that σCm is independent of atomic number. Reference 2 only states that σCm decreases with increasing energy while reference 3 suggests that it is inversely proportional to photon energy.
The simplified model for μ used in the applet is given by
μm=(τ0(Z/Z0)3(E0/E)3+σ0(E0/E))
where τ0 and σ0 are the contributions of the photoelectric effect and the Compton effect at the reference atomic number Z0 and reference photon energy E0. The following values are used
| Z0 | 20 |
| E0 | 100 keV |
| τ0 | 0.085 cm2/g |
| σ0 | 0.2 cm2/g |
This discussion does not take into acount reduced interaction at lower energies due to insufficient X-ray photon enery to overcome the binding energy of the electrons (which produce the absorption edge features). As a result, the simple model used here will over estimate the photoelectric absorption of X-rays for higher Z materials at low to intermediate energies. While this model is inadequate for accurate modeling of X-ray interaction with matter, is is sufficiently accurate to provide the qualitative behaviour students will be exploring with this applet.
The graph below compares the simple model of μm with the experimental data from reference 1:
Other Resources
Version:
- http://weelookang.blogspot.sg/2016/04/x-ray-differential-xray-absorption-by.html Blogpost by Loo Kang Wee
- http://www.compadre.org/osp/items/detail.cfm?ID=13390 original simulation by Michael R. Gallis
end faq
Testimonials (0)
There are no testimonials available for viewing. Login to deploy the article and be the first to submit your review!
You have to login first to see this stats.




