About
![]()
Note: When running this simulation on a tablet or smart-phone, set the parameters, then press the Play button. When running this simulation on a computer, be sure to check “No sensor,” then set the parameters and press the Play button.
Block On An Incline
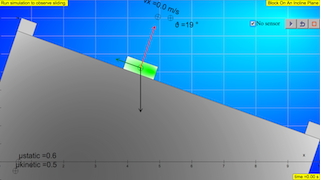
The Block Sliding On An Incline Plane mobile JavaScript model illustrates the forces and dynamics of a block sliding on a surface. This simulation uses the accelerometer on your mobile device to read the direction of the gravitation field g. You may need to lock the orientation of your screen to maintain a fixed view as you tilt your device. For use on computers without an accelerometer or for classroom use, the "No sensor" mode simulates a tilted device in the view.
A force body (free body) diagram showing the normal force (red), the gravitational force (black), and the force of friction (green) is shown. Users can set the initial position and velocity and can adjust both the static and kinetic coefficient of friction when the simulation is paused. Test your knowledge of incline plane dynamics by answering the following questions and comparing your answers with the simulation results. Remember to press the play button after you set the initial values.
Initial values, such as x0 and v0, can be set when the simulation is paused but not when the simulation is running. (Non-editable input fields have a grey background.) You may also drag the block when the simulation is paused. The reset button returns the system to its default state while the reset time button returns the system to the previous values of x0 and v0.
Physics Exercises:
- Draw a force body diagram for a block on a horizontal surface (θ = 0°), labeling all forces.
- Draw a force body diagram for a block on a surface inclined at an arbitrary nonzero angle of θ, labeling all forces.
- The formula for the force of friction f when the block is not slipping is often given in textbooks as f = μsN where N is the magnitude of the normal force. But the simulation shows that the force of friction changes as the surface tilts. Explain why the force of friction is not constant.
- What happens in the simulation if you set μs less than μk? Give a physical reason why the response is reasonable. What happens in the simulation if you set μs or μk less than zero? Give a physical reason why the response is reasonable.
- Derive an expression for the maximum tilt angle without the block slipping (vx= 0) when μs= {0.5, 0.6, 0.8, 1.0, 5.0}. Verify with the simulation. Note that the maximum allowed value of μs is five in this simulation.
- The block is constrained to move from x = 1 (m) to x = 9 (m) by the end bumpers. Suppose ϴ = 0°, and the block is given an initial speed, v = 3 m/s to the right. Derive an expression for how far the block will move. Verify with the simulation if the static coefficient of friction is μs= 0.5 and the kinetic coefficient of friction is μk= 0.4.
- Suppose θ = -30°, and the block starts from rest at x = 1 (m) with a speed of 3 (m/s) up the incline. Derive an expression for how far the block moves up the incline. Verify with the simulation if μs= 0.6 and the kinetic coefficient of friction is μk= 0.4.
- Suppose θ = +30°, and the block starts from rest at x = 1 (m) with a speed of 1 (m/s) down the incline. Will the block stop before it reaches the end bumper if μs= 0.6 and the kinetic coefficient of friction is μk= 0.4? If not, what is the speed when the block reaches the bumper. Derive an expression for the block to move at constant speed down the incline and verify with the simulation.
- Suppose θ = +30°, and the block starts from rest at x = 1 (m) with a speed of 1 (m/s) down the incline. Derive a value for μk for the block to stop sliding just before it reaches the end bumper. Verify with the simulation.
Note: Because continuously reading the accelerometer may drain the battery on a mobile device, you must run the simulation to read the device tilt. The simulation will automatically pause after 4 minutes to conserve battery power.
Credits:
The Block Sliding On An Incline Plane mobile JavaScript model was developed by Wolfgang Christian using version 5 of the Easy Java Simulations (EJS 5) modeling tool. Although EJS is a Java program, EJS 5 creates stand alone JavaScript programs that run in almost any browser. Information about EJS is available at: <http://www.um.es/fem/Ejs/> and in the AAPT-ComPADRE Open Source Physics collection <http://www.compadre.org/OSP/>.
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits

 Wolfgang Christian; Loo Kang Wee
Wolfgang Christian; Loo Kang Wee
end faq
About
![]()
Note: When running this simulation on a tablet or smart-phone, set the parameters, then press the Play button. When running this simulation on a computer, be sure to check “No sensor,” then set the parameters and press the Play button.
Block On An Incline
The Block Sliding On An Incline Plane mobile JavaScript model illustrates the forces and dynamics of a block sliding on a surface. This simulation uses the accelerometer on your mobile device to read the direction of the gravitation field g. You may need to lock the orientation of your screen to maintain a fixed view as you tilt your device. For use on computers without an accelerometer or for classroom use, the "No sensor" mode simulates a tilted device in the view.
A force body (free body) diagram showing the normal force (red), the gravitational force (black), and the force of friction (green) is shown. Users can set the initial position and velocity and can adjust both the static and kinetic coefficient of friction when the simulation is paused. Test your knowledge of incline plane dynamics by answering the following questions and comparing your answers with the simulation results. Remember to press the play button after you set the initial values.
Initial values, such as x0 and v0, can be set when the simulation is paused but not when the simulation is running. (Non-editable input fields have a grey background.) You may also drag the block when the simulation is paused. The reset button returns the system to its default state while the reset time button returns the system to the previous values of x0 and v0.
Physics Exercises:
- Draw a force body diagram for a block on a horizontal surface (θ = 0°), labeling all forces.
- Draw a force body diagram for a block on a surface inclined at an arbitrary nonzero angle of θ, labeling all forces.
- The formula for the force of friction f when the block is not slipping is often given in textbooks as f = μsN where N is the magnitude of the normal force. But the simulation shows that the force of friction changes as the surface tilts. Explain why the force of friction is not constant.
- What happens in the simulation if you set μs less than μk? Give a physical reason why the response is reasonable. What happens in the simulation if you set μs or μk less than zero? Give a physical reason why the response is reasonable.
- Derive an expression for the maximum tilt angle without the block slipping (vx= 0) when μs= {0.5, 0.6, 0.8, 1.0, 5.0}. Verify with the simulation. Note that the maximum allowed value of μs is five in this simulation.
- The block is constrained to move from x = 1 (m) to x = 9 (m) by the end bumpers. Suppose ϴ = 0°, and the block is given an initial speed, v = 3 m/s to the right. Derive an expression for how far the block will move. Verify with the simulation if the static coefficient of friction is μs= 0.5 and the kinetic coefficient of friction is μk= 0.4.
- Suppose θ = -30°, and the block starts from rest at x = 1 (m) with a speed of 3 (m/s) up the incline. Derive an expression for how far the block moves up the incline. Verify with the simulation if μs= 0.6 and the kinetic coefficient of friction is μk= 0.4.
- Suppose θ = +30°, and the block starts from rest at x = 1 (m) with a speed of 1 (m/s) down the incline. Will the block stop before it reaches the end bumper if μs= 0.6 and the kinetic coefficient of friction is μk= 0.4? If not, what is the speed when the block reaches the bumper. Derive an expression for the block to move at constant speed down the incline and verify with the simulation.
- Suppose θ = +30°, and the block starts from rest at x = 1 (m) with a speed of 1 (m/s) down the incline. Derive a value for μk for the block to stop sliding just before it reaches the end bumper. Verify with the simulation.
Note: Because continuously reading the accelerometer may drain the battery on a mobile device, you must run the simulation to read the device tilt. The simulation will automatically pause after 4 minutes to conserve battery power.
Credits:
The Block Sliding On An Incline Plane mobile JavaScript model was developed by Wolfgang Christian using version 5 of the Easy Java Simulations (EJS 5) modeling tool. Although EJS is a Java program, EJS 5 creates stand alone JavaScript programs that run in almost any browser. Information about EJS is available at: <http://www.um.es/fem/Ejs/> and in the AAPT-ComPADRE Open Source Physics collection <http://www.compadre.org/OSP/>.
Version:
- http://www.opensourcephysics.org/items/detail.cfm?ID=14054 Wolfgang Christian, Colleen L. Countryman, and Francisco Esquembre
Other Resources:
- https://www.geogebra.org/m/Stu7gKyg Rotation: Rolling Motion by ukukuku
end faq
Testimonials (0)
There are no testimonials available for viewing. Login to deploy the article and be the first to submit your review!
You have to login first to see this stats.