Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits


![]()
 This email address is being protected from spambots. You need JavaScript enabled to view it.; Francisco Esquembre; Wolfgang Christian; Flix Jess Garcia Clemente
This email address is being protected from spambots. You need JavaScript enabled to view it.; Francisco Esquembre; Wolfgang Christian; Flix Jess Garcia Clemente
end faq
Apps
https://play.google.com/store/apps/details?id=com.ionicframework.kinematicsapp414497

https://itunes.apple.com/us/app/kinematics-simulator/id1190809767?mt=8
Learning Objectives
Candidates should be able to:
(a) define and use displacement, speed, velocity and acceleration
(b) use graphical methods to represent distance, displacement, speed, velocity and acceleration
(c) identify and use the physical quantities from the gradients of displacement-time graphs and areas under and gradients of velocity-time graphs, including cases of non-uniform acceleration
(d) derive, from the definitions of velocity and acceleration, equations which represent uniformly accelerated motion in a straight line
(e) solve problems using equations which represent uniformly accelerated motion in a straight line, including the motion of bodies falling in a uniform gravitational field without air resistance
(f) describe qualitatively the motion of bodies falling in a uniform gravitational field with air resistance
(g) describe and explain motion due to a uniform velocity in one direction and a uniform acceleration in a perpendicular direction.
Practice
https://goo.gl/forms/hreYmzgHZpmhwCxw1
Key inquiry question:
How can we describe the motion of objects moving in a straight line?
1. Speed, velocity and acceleration
• Physical quantities can be scalar (e.g. distance, speed) or vector (e.g. displacement, velocity, acceleration) quantities. Scalar quantities can be added algebraically. Vector quantities can be added using graphical methods (parallelogram method or ‘head-to-tail’ method).
• Average speed of a body is given by total distance travelled / total time taken (v = d/t). Instantaneous speed is the speed at any instant.
• Acceleration of a body is defined as its change in velocity / time taken (a = (v - u)/t). The direction of acceleration is the direction of the change in velocity.
• Acceleration is: zero when velocity is constant (i.e. no change in velocity); positive (object is accelerating) when velocity is increasing; negative (object is decelerating) when velocity is decreasing
2. Graphical analysis of motion
• Displacement-time and velocity-time graphs of a body allow us to deduce when the body is: at rest; moving with uniform velocity and acceleration; moving with non-uniform velocity and acceleration.
• Gradient of a displacement-time graph gives the velocity of the moving object; Gradient of a velocitytime graph gives the acceleration of the moving object; Area under a velocity-time graph gives the displacement travelled by a body.
Students’ prior knowledge of Kinematics
Primary level:
Students will not have been introduced to the concepts to describe motion. They would have knowledge of the effects of a force to stop or move an object; change its speed (move faster or slower) or direction of motion.
Lower secondary level:
Students learn that speed:
• is a measure of how fast an object is moving;
• depends on the distance (length) travelled and the time taken (unit: m/s).
Objects usually do not move at the same speed, hence, it is more useful to measure its average speed which is defined as total distance travelled / total time taken. Speed at any instant is the average speed over an extremely short time interval.
Students’ common misconceptions and learning difficulties in Kinematics
Displacement, velocity and acceleration:
Students’ concepts of displacement, velocity, and acceleration are not well differentiated.
They often think that: same position means same velocity for two objects; same velocity means same acceleration for two objects; larger (or smaller) velocity means larger (or smaller) acceleration; zero velocity means zero acceleration; and acceleration and velocity are always in the same direction.
Displacement-time and velocity-time graphs: Students often view the position and velocity graphs as the actual path of the object, rather than a graphical representation of an object’s motion
Worksheet
- ejss_model_kinematics Motion in One Dimension student worksheet (2017)v3dl.docx by Dave
- ejss_model_kinematics CT_kinematics (1017).ppt 2017 by Dave
- ejss_model_kinematics Motion in One Dimension student worksheet (2017).docx 2017 by Dave
- Slides for Workshop Link1 , Link2 2016
- Final version Link1, Link2 by Lyna, Gavin, Dave and lookang 2016
- Motion in One Dimension student worksheet (dl-gwf) Link1, Link2 by Lyna, Gavin, Dave and lookang 2016
Video
- https://youtu.be/ZYIeBKDBXU8 Kinematics 1d simulation video tutorial with modeling pedagogy by lookang lawrence wee
- https://youtu.be/SsSPd6I4BnA Kinematics 1D simulation running on hmtl5 Modeling pedagogy 2 by lookang lawrence wee
- Kinematics Simulation - Secondary & JC by Dave Lommen
- https://www.youtube.com/watch?v=96gBQqgWwkM by ETDtogo
- https://www.youtube.com/watch?v=-RfbnnqgOvk by ETDtogo
Pedagogical Writeup
| Process | Lesson Implementation | |
| Sub-Process(es) | Introducing the Lesson / Arousing and Sustaining Interest | |
| Teaching Action | Mystery | |
Technology:
mystery could take the form an describe it all equation, called model.
Give the challenge to solve the mystery of a predictive equation that can be use to tell the future, more precisely the movement of a car, in a physics lesson.
Through the model selected by the students, it gives an indication of the students prior knowledge about what they know now, so that the teacher can understand the gaps of understanding for personalised mentoring http://iwant2study.org/ospsg/index.php/interactive-resources/physics/02-newtonian-mechanics/01-kinematics/38-kinematics-1d
| Process | Lesson Implementation | |
| Sub-Process(es) | Introducing the Lesson / Arousing and Sustaining Interest | |
| Teaching Action | Little Professor/Little Teachers | |
Technology:
use exisiting schools' learning management system such as https://www.edmodo.com/ or Whatapp group chat to allow of arousing and sustaining interest.
Other simulations
- http://www.physicsclassroom.com/Physics-Interactives/1-D-Kinematics/Graphs-and-Ramps
- http://www.thephysicsaviary.com/Physics/Programs/Labs/EquationsOfMotionLab/index.html
- http://ophysics.com/k5.html by This email address is being protected from spambots. You need JavaScript enabled to view it.
- http://ophysics.com/k6.html by This email address is being protected from spambots. You need JavaScript enabled to view it.
Project related:
- AEP 03/16 LW Apps as Virtual Lab
- Understanding Teacher Learning Community as Support for Implementation of Open Source Physics for Conceptual Instruction Project Number: OER 10/15 GWF Project Duration: 01 July 2015 - 30 April 2017 http://weelookang.blogspot.sg/2015/07/understanding-teacher-learning.html
Family of Resources
| Secondary | Primary | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
About
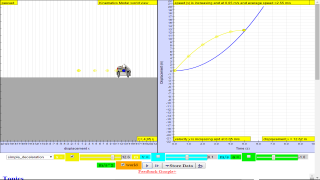
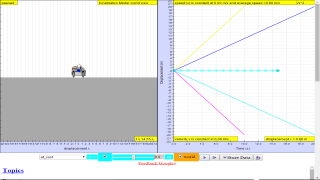
TopicsKinematicsSpeed, velocity and acceleration Graphical analysis of motion DescriptionThis simulation has a drop-down menu for exploration of(i) at rest use of progressive mathematical model is encouraged X = 0 for example (ii) moving with uniform velocity, use of progressive mathematical model is encouraged for example X = 1*t for a constant velocity motion of v =1 m/s (iii) moving with non-uniform velocity (eg, constant acceleration) use of progressive mathematical model is encouraged for example X = 0.5*1*t^2 for a constant acceleration motion of a =1 m/s^2 When only the velocity-time graph check-box is selected, it can be explored for the following cases too. (i) at rest , (ii) moving with uniform velocity (eg, no acceleration) (iii) moving with uniform acceleration (eg, constant acceleration = 9.81 m/s^2) Sample Learning Goals
(e) plot and interpret a displacement-time graph and a velocity-time
graph
(f) deduce from the shape of a displacement-time graph when a body is: (i) at rest example of progressive mathematical model is encouraged X = 0 (ii) moving with uniform velocity example of progressive mathematical model is encouraged X = 1*t for a constant velocity motion of v =1 m/s (iii) moving with non-uniform velocity example of X = 0.5*1*t^2 for a constant acceleration motion of a =1 m/s^2 (g) deduce from the shape of a velocity-time graph when a body is: (i) at rest (ii) moving with uniform velocity (iii) moving with uniform acceleration (iv) moving with non-uniform acceleration Version:Translations
Software Requirements
Credits
end faq |
About
TopicsKinematicsSpeed, velocity and acceleration Graphical analysis of motion DescriptionThis simulation has a drop-down menu for exploration of(i) at rest use of progressive mathematical model is encouraged X = 0 for example (ii) moving with uniform velocity, use of progressive mathematical model is encouraged for example X = 1*t for a constant velocity motion of v =1 m/s (iii) moving with non-uniform velocity (eg, constant acceleration) use of progressive mathematical model is encouraged for example X = 0.5*1*t^2 for a constant acceleration motion of a =1 m/s^2 When only the velocity-time graph check-box is selected, it can be explored for the following cases too. (i) at rest , (ii) moving with uniform velocity (eg, no acceleration) (iii) moving with uniform acceleration (eg, constant acceleration = 9.81 m/s^2) Sample Learning Goals
(e) plot and interpret a displacement-time graph and a velocity-time
graph
(f) deduce from the shape of a displacement-time graph when a body is: (i) at rest example of progressive mathematical model is encouraged X = 0 (ii) moving with uniform velocity example of progressive mathematical model is encouraged X = 1*t for a constant velocity motion of v =1 m/s (iii) moving with non-uniform velocity example of X = 0.5*1*t^2 for a constant acceleration motion of a =1 m/s^2 (g) deduce from the shape of a velocity-time graph when a body is: (i) at rest (ii) moving with uniform velocity (iii) moving with uniform acceleration (iv) moving with non-uniform acceleration Version:Translations
Software Requirements
Credits
end faq
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
end faq


.png
)