About
Using The Beach Ball Physics Model
 The physics of a thrown beach ball can be very interesting. Because of
its relatively low mass (compared to its size), subtle effects that are
important in sports like baseball, soccer and volleyball become
exaggerated in the beach ball’s motion. This simulation allows users to
explore a simple model of several “complications” to simple projectile
motion: drag, buoyancy and the Magnus effect. Drag slows the ball down,
buoyancy makes the ball “float” and the Magnus effect puts a curve on
the ball’s trajectory.
The physics of a thrown beach ball can be very interesting. Because of
its relatively low mass (compared to its size), subtle effects that are
important in sports like baseball, soccer and volleyball become
exaggerated in the beach ball’s motion. This simulation allows users to
explore a simple model of several “complications” to simple projectile
motion: drag, buoyancy and the Magnus effect. Drag slows the ball down,
buoyancy makes the ball “float” and the Magnus effect puts a curve on
the ball’s trajectory.
Simulation Controls:
The simulations main display includes an interactive 3-D display of the ball in flight. The “Show Velocity” checkbox will add a pair of vectors for the ball’s velocity and angular velocity (both scaled to the ball’s launch speed). The “Show Forces” checkbox adds vectors for all the forces contributing to the ball’s dynamics. A pair of graphs may be hidden or viewed for ancillary information using the Show Graphs checkbox.
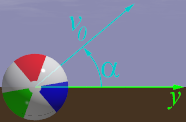 The basic ball launch parameters are the initial height of the ball, the
launch speed and the launch angle α (from horizontal).
The basic ball launch parameters are the initial height of the ball, the
launch speed and the launch angle α (from horizontal).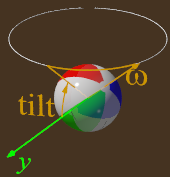
Beach Balls come in various sizes, so the radius and mass of the ball can be specified. Note that the assumption is that the mass given is what would be measured on a balance; the mass of the air inside the ball does not affect such measurements as its weight is offset by the buoyancy due to the displaced volume of air. To see the buoyant force in a simple way, note that if you weigh your beach ball empty or inflated, you will get the same measurement and yet the inflated ball’s contents do contribute to the overall inertia.
The simulation also allows the adjustment of some of the aerodynamic parameters. See the technical notes for discussion. For those interested in the aerodynamics, the Reynolds number and Spin factor are also displayed.
The Physics of Beach Ball Trajectories: Technical Notes
The model employed in this simulation follows Clanet’s “Sports Ballistics”.1 This simulation takes up as the positive z direction and the initial velocity of the ball to be in the y-z plane.
Gravity and Buoyancy
In a Physics Teacher paper on the vertical motion accounting for aerodynamic effects, Timmerman and van der Weele2 note
“… we include the buoyant force, which is almost always forgotten or
ignored in the literature on this topic. This is somewhat curious, since
the medium that is responsible for the drag force at the same time
introduces a buoyant force.”
The mass (and hence the weight) of a beach ball are easy to determine: just place it on an electronic balance. The same results will be obtained whether the ball is inflated or not. When a ball is thrown, the air inside goes for a ride as well, and in the case of a beach ball, this is a significant contribution to inertia:
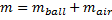
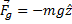
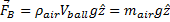
Drag Force
Drag force, or air resistance is the friction effect of moving though the air. It will be a significant force for almost any toss of the beach ball. The drag force is opposes motion and it is modeled in this simulation by
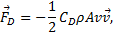 ,
,

Magnus Effect
The Magnus force is very noticeable when it is used to make the trajectory of a ball curve while in flight. The size of the effect depends upon both the velocity and angular velocity of the ball, and the direction is always perpendicular to both the velocity and the rotation axis of the ball’s spin. The force is often referred to as lift, and (following Clanet) is given by:
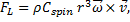
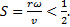
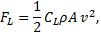
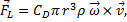
Complete Model Dynamics
The full beach ball dynamics used in the model is given by
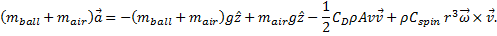
(1) Sports Ballistics by Clanet, Christophe, Annual Review of Fluid Mechanics, 01/2015, Volume 47, Issue 1
(2) On the rise and fall of a ball with linear or quadratic drag by Timmerman, Peter; Weele, van der, Jacobus P, American Journal of Physics, 1999, Volume 67, Issue 6
(3) For more information on drag, see https://en.wikipedia.org/wiki/Drag_coefficient
(4) Nathan AM. 2008. The effect of spin on the flight of a baseball. Am. J. Phys. 76:119–24
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits

 Michael R. Gallis, Ryan Vidal; lookang
Michael R. Gallis, Ryan Vidal; lookang
Sample Learning Goals
[text]
For Teachers
[text]
Research
[text]
Video
Backspin Basketball Flies Off Dam by Veritasium
Physics of toys- Cup Flyers // Homemade Science with Bruce Yeany by Bruce Yeany
Version
https://weelookang.blogspot.com/2020/03/beach-ball-physics-for-sports.html

Question 1: A student claims that having a backspin on the ball increases the distance travelled by the ball as compared to having a top spin. True or false?
True. Backspin causes the ball to travel further than with having a top spin.
Question 2: Taking the default point of reference from the sim (blue arrow points up, red arrow points towards user, and green arrow towards right of user), how does having a left spin affect the trajectory of the ball?
Ball moves to the right and also away from the user.
Question 3: If a tennis player hit the ball with a certain spin and it reached the ground faster than expected, what type of spin did the ball experience? (assuming the tennis ball in this case is modelled by the same ball in the sim)
Top spin. This exerts a downward force on the ball and thus makes it hit the ground faster.
Other Resources
[text]
end faq
{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}
- Details
- Written by Jonathan
- Parent Category: Physical & Sports Education
- Category: Physical Education
- Hits: 3121