About
In physics and engineering, a ripple tank is a shallow glass tank of water used in schools and colleges to demonstrate the basic properties of waves. It is a specialized form of a wave tank. The ripple tank is usually illuminated from above, so that the light shines through the water. Some small ripple tanks fit onto the top of an overhead projector, i.e. they are illuminated from below. The ripples on the water show up as shadows on the screen underneath the tank. All the basic properties of waves, including reflection, refraction,interference and diffraction, can be demonstrated.
Ripples may be generated by a piece of wood that is suspended above the tank on elastic bands so that it is just touching the surface. Screwed to wood is a motor that has an off centre weight attached to the axle. As the axle rotates the motor wobbles, shaking the wood and generating ripples.
What is a Two-Source Interference (Ripple Tank)?
An example of two-source interference can be observed in a ripple tank.
 |
| (Fig. 1) Two dippers S1 and S2 are attached to the vibrator of the ripple tank. |
1. Two dippers S1 and S2 are attached to the vibrator of the ripple tank. (Fig. 1)
2. Each dipper, when oscillates vertically, generates circular waves. (Fig. 2)
 |
| Fig. 2 show Source S1 that creates a circular waves |
 |
| Fig. 2 show Source S2 that creates a circular waves |
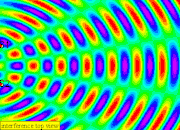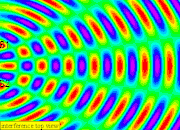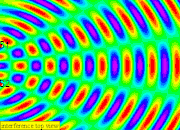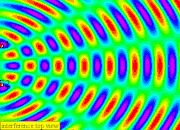
3. When the two waves meet, they interfere where each dipper's generated circular waves which superposition with one another.
 |
| resultant wave form due to the superposition of each wave generated by S1 and S2. |
1 to 3 in animation would look like this.
 |
| Source S1 that creates a circular waves |
 |
| Source S2 that creates a circular waves |
 |
| resultant wave form due to the superposition of each wave generated by S1 and S2 |
4. Between the two dippers, a stationary wave is formed due to constructive and destructive interference
 |
| stationary wave is formed in between S1 and S2 |
 |
| stationary wave is formed in between S1 and S2 (look closely at the wave formation in between S1 and S2 |
5. When normal white light shines on the ripple tank with the interference pattern
6. The positions where the waves meet that cancel out are called nodes, it is rather difficult to see so i will explain in terms of a spectrum visualization as always green due to (eg. peak meet trough) destructive interference occurs (i.e. source waves arrive in anti-phase)
 |
| the green parts are called nodes where the 2 waves meet destructively to create zero displacement |
7. The anti-nodes will be alternating between bright (eg. peak meet peak ) and dark (eg. trough meet trough) for White and Black visualization or Red (eg. peak meet peak ) and Blue (eg. trough meet trough) due to constructive interference (i.e. source waves arrive in phase). note that (peak meet peak ) and (trough meet trough) is constructive.
8. The lines passing through a series of nodes are called the nodal lines
 |
| nodal lines and antinodal lines picture by leongster |
9. The lines passing through a series of anti-nodes are called the antinodal lines
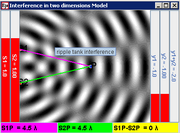
10. for example, the distance between point P and S1, S1P = 4.5 λ and S2P = 4.5 λ, therefore path difference between the sources, S2P –S1P = 0 for a constructive (trough meet trough) dark interference.
 |
| S1P = 4.5 λ |
 |
| S2P = 4.5 λ |
 |
| S2P –S1P = 0. |
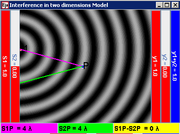
11. for example, the distance between point P and S1, S1P = 4.0 λ and S2P = 4.0 λ, therefore path difference between the sources, S2P –S1P = 0 for a constructive (peak meet peak) bright interference.
 |
| S1P = 4.0 λ |
 |
| S2P = 4.0 λ |
 |
| S2P –S1P = 0 |
12. for example, the distance between point P and S1, S1P = 5.0 λ and S2P = 5.5 λ, therefore path difference between the sources, S2P –S1P = 0.5 λ for a destructive interference.
 |
| S1P = 5.0 λ |
 |
| S2P = 5.5 λ |
 |
| |S1P –S2P| = 0.5 λ |
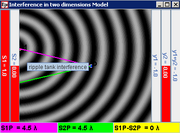
13. for example, the distance between point P and S1, S1P = 4.5 λ and S2P = 5.0 λ, therefore path difference between the sources, S2P –S1P = 0.5 λ for a destructive interference.
 |
| S1P = 4.5 λ |
 |
| S2P = 5.0 λ |
 |
| |S1P –S2P| = 0.5 λ |
In Conclusion, when the sources are in phase
condition for constructive interference: ∆L = m λ, where m = 0, 1, 2, ...
condition for destructive interference: ∆L = (m + 0.5) λ, where m = 0, 1, 2, ...
You can explore the applet for the cases when the sources are in anti-phase yourself !
For Teachers
https://sites.google.com/site/ijcsuperposition/
http://www.seab.gov.sg/aLevel/20102011Syllabus/9646_2011.pdf
SECTION lV WAVES Superposition
(f) show an understanding of the terms interference and coherence.
(g) show an understanding of experiments which demonstrate two-source interference using water, light and microwaves.
Software Requirements
Java
Real Setup
http://en.wikipedia.org/wiki/Ripple_tank
 |
| http://en.wikipedia.org/wiki/File:Simple_ripple_tank.svg#globalusage by Cryonic07 |
 |
| A small 650W incandescent light source was mounted about one meter above the tank, and the ripples projected on the screen were photographed from the side (see lower picture on the right) using a high-speed video camera from http://livephoto.rit.edu/LPVideos/ripple/. |
http://livephoto.rit.edu/LPVideos/ripple/Ripple_Tank_Waves_1.mov
a video suitable for video analysis using tracker?
Credits
Andrew Duffy, Juan M. Aguirregabiria, Fu-Kwun Hwang and Loo Kang Wee
Video
Physics Lab Demo 14: Ripple Tank by CarletonPhysics
Version
- http://iwant2study.org/lookangejss/04waves_11superposition/ejs/ejs_model_Ripple_Tank_Interferencewee13.jar Java Model by Andrew Duffy, Juan M. Aguirregabiria, Fu-Kwun Hwang and Loo Kang Wee
- http://weelookang.blogspot.sg/2011/01/ejs-open-source-ripple-tank.html Java version
- http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=2067.0 NTNU Java Forum by Loo Kang Wee
- http://www.compadre.org/osp/items/detail.cfm?ID=9989 Interference Model: Ripple Tank written by Andrew Duffy Original
- Juan M. Aguirregabiria for his screen patterns codes instantaneous patterns and average intensity patterns
Other resources
- ther great simulation is http://phet.colorado.edu/en/simulation/wave-interference http://phet.colorado.edu/en/simulation/wave-interference
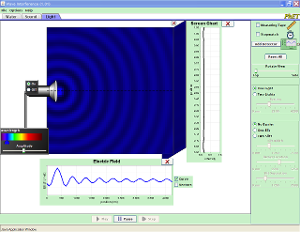 Like: a lot of possibilities very complex and realistic
Like: a lot of possibilities very complex and realistic - http://www.cabrillo.edu/~jmccullough/Physics/Interference_Wave_Nature.html collection of good applets
- https://www.geogebra.org/m/XdW2SjQ8 by ukukuku