About
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits

 Fu-Kwun Hwang - Dept. of Physics, National Taiwan Normal Univ.; lookang
Fu-Kwun Hwang - Dept. of Physics, National Taiwan Normal Univ.; lookang
end faq
Theory
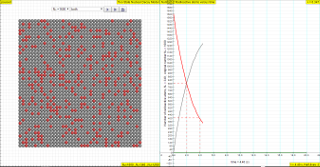
The law of radioactive decay predicts how the number of the not decayed nuclei of a given radioactive substance decreases in the course of time. The GREY circles of this simulation symbolize 100 (variable selectable up 400 or 1024) to atomic nuclei of a radioactive substance whose half-life period (T1/2) amounts to 0.1 to 3.0 seconds. The scientfic graph on the right, in number of radioactive atoms versus time, RED trail represents represents the Number of radioactive atoms, N₁ not yet decayed nuclei at a given time t, predicted by the following law:
N1 = N0 e -(ln2/T1/2)) t
when you play with the show model option, show me N1= No*exp(-ln(2)/T1/2*t)
similarly it is possible to also predict the number of decayed atoms using the formula
N2 = N0 -N0 e -(ln2/T1/2)) t
when you play with the show model option, show me N2 = No-No*exp(-ln(2)/T1/2*t)
in the option both2 when selected, can display the rate of radioactive atoms versus time,
dN = pN0 e -(ln2/T1/2)) t
when you play with the show model option, show me dN = p*N0*exp(-ln(2)/T1/2*t)
the terms use are
N1 .... number of the not decayed nuclei
N2 .... number of the decayed nuclei
N0 ... number of the initially existing nuclei at time, t = 0
t .... time
T1/2 .... is the time taken for the activity of a given amount of a radioactive substance to decay to half of its initial value
λ, or sometimes also known as "lambda" the inverse of the mean lifetime, sometimes referred to as simply decay rate.
p is probability of decaying where 0 means no chance at all, 1 is 100% chance of decaying
Formula that related some of these terms are
T1/2 = ln(2)/λ
\( \lambda = \frac{p}{dt} \)
The Ordinary Differential equations used is
\( \frac{dN_{1}}{dt} = - \lambda_{1}N_{1} \)
Versions
- http://weelookang.blogspot.sg/2016/02/a-comparison-of-2-javascript-nuclear.html comparison of 2 HTML5 versions
- http://weelookang.blogspot.sg/2015/12/ejss-radioactive-decay-model.html lookang's blogpost about this JavaScript version
- http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=194.0 by Fu-Kwun Hwang original Java version
- http://www.opensourcephysics.org/items/detail.cfm?ID=10576 by Wolfgang Christian similar Java version
Other Resources
- http://www.opensourcephysics.org/items/detail.cfm?ID=13978&S=7 Two-State Nuclear Decay JS Model written by Wolfgang Christian
- http://www.walter-fendt.de/html5/phen/lawdecay_en.htm by Walter fendt