About
Symmetry operations
Rotation, mirroring and inversion are noncommutative and hence non Abelian transformation operations in set theory. The result depends on the sequence of operations.
The simulation demonstrates this for the operations of rotation and mirroring, applied to a triangle.
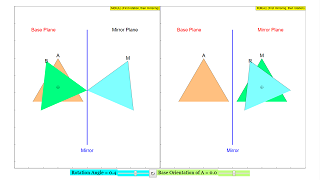
When the simulation is started, one sees two identical coordinate systems, with a mirror located at the center x = 0 of each. At its left side there is a triangle with its base initially parallel to the x axis. Its upper edge is marked by the letter A. The triangle is pink in color. At the right side of the mirror one sees the mirror image of the triangle, marked by a letter M, and colored in blue
The slider Base Orientation defines the orientation of the original triangle. One observes the counterclockwise rotation of the mirror image, which is the same in both charts.
The slider Rotation Angle creates a rotation operation on the object in its base orientation.
In the left chart the rotation is operated on the object A, and the mirror image M of the rotated object R is displayed. In the right chart the rotation is operated on the mirrored object M and results in a different R. The sequence of operations is discernable by the coloring of the triangles: green is first, blue is second.
The left chart displays the mirrored-rotated object, the right one the rotated-mirrored object. In general both are different in orientation. The transformation operations are noncommutative.
Reset restores the initial orientation.
This file was created by Dieter Roess in November 2009
This simulation is part of
“Learning and Teaching Mathematics using Simulations
– Plus 2000 Examples from Physics”
ISBN 978-3-11-025005-3, Walter de Gruyter GmbH & Co. KG
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits
 Dieter Roess - WEH- Foundation; Tan Wei Chiong; Loo Kang Wee
Dieter Roess - WEH- Foundation; Tan Wei Chiong; Loo Kang Wee
Sample Learning Goals
[text]
For Teachers
If you first apply a rotation to a object, then mirror that rotated object, you'll find that what you get is different than if you first applied the mirroring, then the rotation.
There are two panels in this simulation: the left panel shows what happens when you first apply rotation, then the mirroring. the right panel shows what happens when the mirroring is first applied, then the rotation.
The rotation and base orientation of the triangle A can be adjusted using the sliders provided.
Research
[text]
Video
[text]
Version:
- http://weelookang.blogspot.sg/2016/02/vector-addition-b-c-model-with.html improved version with joseph chua's inputs
- http://weelookang.blogspot.sg/2014/10/vector-addition-model.html original simulation by lookang
Other Resources
[text]
end faq
{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}
- Details
- Written by Wei Chiong
- Parent Category: Mathematics
- Category: Numbers and Algebra
- Hits: 3916